巧用均值不等式 妙解高中數學題

黃盛浩

(福建省上杭縣第二中學 364200)

均值不等式是高中數學不等式的重要內容，應用范圍較為廣泛，借助均值不等式可以很容易地解決數學問題，有著非常好的應用效果.在以往的高考數學中，均值不等式是重要的考查內容，根據題目中的條件，靈活利用均值不等式，掌握相應的技巧和訣竅，結合均值不等式的變形，采取有效的解題策略，完成數學問題思考和解答，提高課堂教學效果和質量.

一、注重恰當系數的湊配

在使用均值不等式解決數學問題時，常常會遇到不便于套用公式的情況，或者題設條件使用不方便.因此，需要根據均值不等式等號成立的條件，對其進行靈活運用，結合均值不等式的等號條件作為基礎，對其系數進行恰當的湊配，完成數學問題的有效解答.

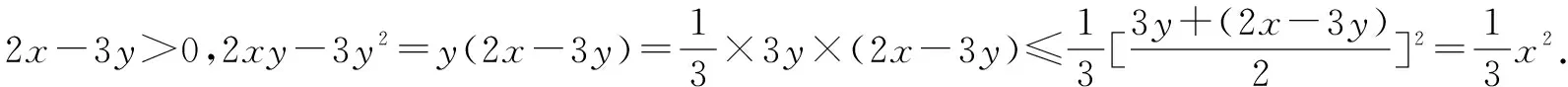
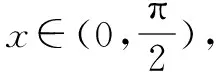
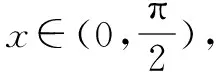
面對高中數學問題，需要對題目進行分析，通過進行系數的湊配，靈活利用均值不等式，完成數學問題解題，提高學生解題效果和質量.

二、注重不同項數的組合搭配

在均值不等式應用中，需要對其項進行合理拆分，或者配湊因式，完成問題的思考和解答.此種方式是均值不等式應用的常用方式，通過相應拆分和拼湊可以實現等號的成立，并且保證每一項都為正值，此時其積則是定值或者其和是定值.

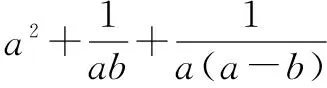
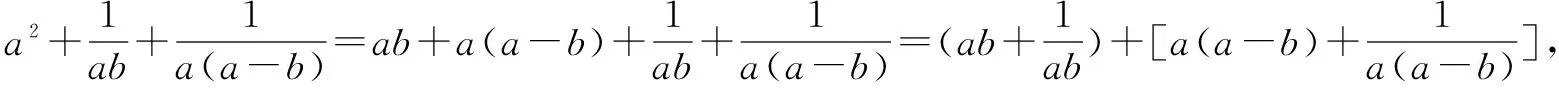
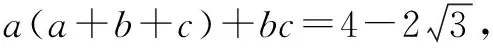
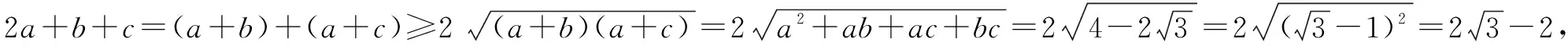
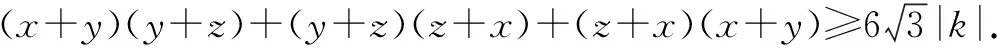
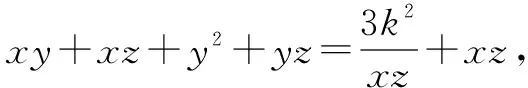
三、借助靈活變形完成解題

高中數學問題解答中，均值不等式的應用，需要對其進行靈活變形，在實際的應用中，需要注重其等式是否成立，結合均值不等式的變形形式，對其進行靈活利用.

例6a、b、c∈R+，并且a+b+c=abc，求a7(bc-1)+b7(ac-1)+c7(ab-1)的值.

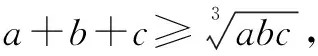
四、靈活利用基本模型和變式

在均值不等式應用到數學解題中，不僅僅需要掌握和利用原始形式，同時需要料及其常見的變形形式和公式逆用等，靈活利用基本模型和變式，完成數學問題解題，提高學生解題能力，保證課堂教學有效開展.

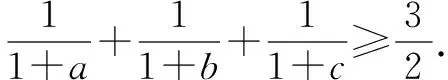
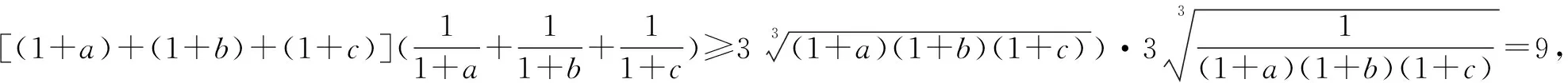
上式當僅當a=b=c=1時取等號.

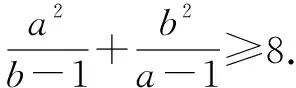
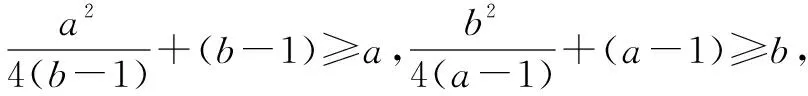
在均值不等式的應用中，需要對其基本模型和變式全面了解和掌握，在實際的解題中，根據題目類型做出相應的選擇，有效解決數學問題.

本文結合相應的數學問題，對均值不等式的應用進行分析，在實際的均值不等式應用中，其關鍵點是分析數學問題本質，通過相應的變形技巧，構建均值不等式結構.在應用中，要求學生熟練掌握策略和技巧，開展相應的學習和訓練，豐富學生解題技巧，加強學生數學素養培養，提高學生數學符號觀察能力，結合數學式符合規律，鍛煉學生的敏感性，保證均值不等式的靈活利用，提高數學問題解題有效性.