例談一題多解在解析幾何中的應用

于慶麗

(江蘇省宿遷市泗洪姜堰高級中學 223900)

新課程視野下高考命題秉持素養立意，多以策略性知識為背景，考查學生必備知識、關鍵能力、學科素養和核心價值，就數學而言最核心的價值就是發展學生的數學素養和提高解決問題的能力.數學名家說過，問題是數學的心臟，思維是數學的靈魂，而方法則是數學的行為，從一個經典的，簡明的數學問題出發，把數學冰冷的美麗轉化成數學火熱的思考.通過多角度，全方位的觀察、感知、分析、嘗試、提煉、綜合，使得數學的思考從聯系、到聯通，再到思維的有效對接，能夠很好地優化解題思路，提升分析問題解決問題的能力.近幾年解析幾何在高考中對計算能力的考查逐年加大，而好的解法能夠簡化運算，所以在平時教學中要注重一題多解在解析幾何中的應用，可以從不同的角度去思考和分析問題，在多種解法中去尋求通解和優解.

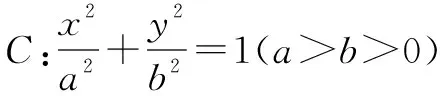
(1) 求橢圓C的標準方程；

(2) 如圖，過點C(0，1)且斜率大于1的直線l與橢圓交于M，N兩點，記直線AM的斜率為k1，直線BN的斜率為k2，若k1=2k2，求直線l斜率的值.

分析(1)根據已知條件，建立方程組，求出a，b，即可得到橢圓的標準方程.

(2)設出直線l方程為y=kx+1，M(x1，y1)，N(x2，y2)，將直線l方程與橢圓方程聯立，求出x1+x2和x1x2，根據條件求出k1和k2，代入k1=2k2化簡計算，得到關于k的方程，解方程求出k的值.

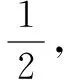
(2)解法一(通過兩邊平方轉化成韋達定理形式)

由橢圓的對稱性可知直線l的斜率一定存在，設其方程為y=kx+1.

設M(x1，y1)，N(x2，y2).

又因為M(x1，y1)，N(x2，y2)在橢圓上，

即3x1x2+10(x1+x2)+12=0.

解法二(通解)

由橢圓的對稱性可知直線l的斜率一定存在，設其方程為y=kx+1.

設M(x1，y1)，N(x2，y2).

kx1x2+(2k+2)(x1+x2)+(2k-3)x2+6=0,

2(kx1+1)(kx2+1)=-3(x1+2)(x2+2),

(2k2+3)x1x2+(2k+6)(x1+x2)+14=0.

解法四(將直線AM與橢圓方程聯立，解出M、N)