“數學建模”在高中數學解題中的應用研究
王洋洋
(北京師范大學(珠海)附屬高級中學 519000)
“數學建模”是利用抽象的數學知識描述具體的現實問題,并依托數學模型分析、解決問題的素養.高中數學教材中蘊含著深刻的建模思想,在教學實踐中,引導學生通過“數學建模”解決問題,能夠有效鍛煉學生的抽象思考能力,提升學生的邏輯推理水平,同時激發學生深入解讀數學知識在社會生產生活中的應用價值,進而達到學以致用教學目的.因此,教師在解題指導中應利用建模思想啟發學生探究解題思路,提高數學核心素養.
一、“數學建模”在高中數學解題中的應用實踐
本文根據高中數學人教A版必修一教材內容,結合函數模型相關例題說明“數學建模”的實踐應用.
例1某燈具城新進一批臺燈,進價20元/臺.臺燈日銷售量為w(臺),且銷售單價x(元)與銷售量之間存在函數關系,即w=-2x+80,如果每日銷售臺燈的利潤為y(元),那么(1)y與x之間存在怎樣的函數關系?如果在保證銷售量最大的前提下,燈具城要想每天獲得150元的利潤,則售價應如何調整?
解答(1)由于每天的銷售利潤等于每臺的利潤乘以銷售量,則有y=(x-20)(-2x+80)=-2x2+120x-1600.
(2)根據題意,令y=150,即-2x2+120x-1600=150,解的x1=25,x2=35,根據w=-2x+80,可知函數單調遞減,即當w增大時,x減小,所以,每臺售價為25元時,燈具城能夠在保證銷售量最大的前提下,每天獲得150元的利潤.
例2某景區為方便游客設置了租車服務.已知景區共投放單車50輛,單車的日常管理費用每天115元,根據數據顯示當單車日租金不高于6元,單車可以全部租出;超過6元,每增加1元,租出的單車就會減少3輛.如果單車日租金x取整數,且景區要求租車日總收入高于日常管理費用,用y表示租車的日凈收入,請問當日租金為多少元,租車的日凈收入最多?
解答根據題意列出y與x的函數關系式,即當x≤6時,y=50x-115,令50x-115>0,解得x>2.3.由于x∈N*,所以x≥3,且3≤x≤6,x∈N*.
當x>6時,y=[50-3(x-6)]x-115.
令[50-3(x-6)]x-115>0,有3x2-68x+115<0,
上述不等式的整數解為2≤x≤20(x∈N*),
所以6 對于y=50x-115(3≤x≤6,x∈N*). 顯然當x=6時,ymax=185(元), 當x=11時,ymax=270(元). 由于270>185, 所以,當每輛自行車的日租金定在11元時,才能使一日的凈收入最多. 例3一電子企業年終報表中反映2010年共生產智能手機2萬部,為擴大生產,該企業計劃從2011年起以 20%的年增速度逐步擴大產量,請問按照這一速度,這家企業從哪一年開始智能手機的年產量超過12萬件? 解答根據題意設該企業的年產量為y,n年后的產量為y=2(1+20%)n. 當該企業產量超過12萬件時,則有y>12,即2(1+20%)n>12,化簡(1.2)n>6. 兩邊以1.2為底取對數,可得n>log1.26,查看對數表可以得出n≈9.8.取整數n=10. 所以,從2020年開始這家工廠生產這種產品的年產量超過 12 萬件. 上述例題結合高中常見問題集中分析了“數學建模”在解題中的運用.當然,“數學建模”的應用并不僅限于此,方程建模、數列建模以及統計學中的相關模型,學生在日常解題遇到的概率也很大.教師在解題指導中,應著重強調對建模思想的滲透,具體來講就是針對建模步驟啟發學生的深入思考,讓學生在規范解題過程中深化對“數學建模”的思考,把握“數學建模”的應用規律,提高自主運用能力. “數學建模”在高中數學解題中的滲透是課程教學指導的重要內容,數學教師為保證教學效果,提升學生的數學思維,提供學生的自主建模、獨立解題能力,應不斷反思“數學建模”過程,提高解題指導效果. “數學建模”不僅是一種解題思路,更是一種數學思想,其中蘊含著深刻的數學理論.學生在解題中運用函數等數學知識很容易,但是形成建模思維卻很難,這不僅需要扎實的數學知識基礎支撐,更需要學生保持對數學探究與應用的興趣.針對此,在解題指導過程中,教師應立足于知識基礎與學習興趣,一方面結合教材完善課程講解,幫助學生深入知識理解,建立完善的知識體系,并把握常見的數學模型;另一方面注重興趣引導,將數學模型與現實問題相結合,激發學生建模興趣,促使學生深入認識實際問題與數學知識之間的關聯性,產生探索數學建模本質的強烈愿望. “數學建模”需要學生分析數學知識抽象運用,更應該注重對教學情境的構建,促使學生一邊建模,一邊體驗利用數學知識和方法的樂趣,并鼓勵學生圍繞建模進行聯想與想象,針對已知問題進行適當變形,拓寬建模的應用范圍,達到舉一反三的學習效果.此外,教師還應強調模型檢驗過程,對于數學問題而言,模型的正確與否直接決定著后續解題過程是否合理,最終答案是否準確.因此,教師應指導學生養成反思與檢驗的好習慣,根據問題中的條件,以及模型自身的特點驗證模型的準確性、合理性,并針對問題做出調整,以提高模型的適用性,提高學生獨立思考以及自主解題能力. 總之,“數學建模”充分體現了學以致用的理念,學生在解題過程中通過建模能夠建立現實問題與抽象數學的關系,并創新探索 解題思路.基于此,教師在日常解題指導中應積極滲透,讓學生在建模過程中提高知識應用意識,提升創新實踐素養.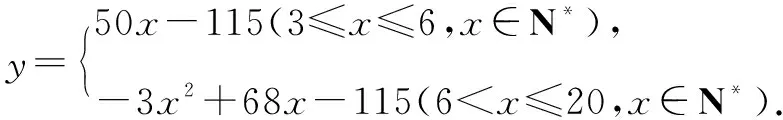
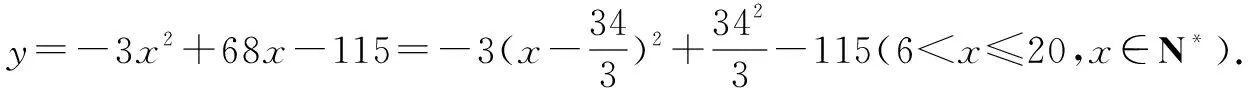
二、“數學建模”在高中數學解題中的應用反思

