合并同類項
——帶電粒子在組合場中運動的求解方法

饒開宏

(湖北省武漢外國語學校 430022)

帶電粒子在組合場中的運動.情景常顯得很復雜，尤其是在周期性變化的電磁場中的運動，給人眼花繚亂的感覺，這里介紹一種破解方法，希望能給大家的教學工作起到一個“拋磚引玉”的啟發作用.

數學中常用到一種合并同類項的方法簡化方程的形式，這里借鑒此法，將帶電粒子在電場和磁場中的運動分割成兩個整體，當做電場中的連續運動和磁場中的連續運動兩個相對獨立的過程.

例1回旋離子加速器，由兩個半徑為R的D型盒，兩D型盒區域加垂直于D型盒的磁感應強度為B的勻強磁場，兩盒之間加如圖2所示規律變化的加速電壓(中間區域為勻強電場)一個電量為q，質量為m的帶電粒子從o點以可忽略的初速進入電場區域，設兩D型盒間距為d，最后一次加速后便直接導出，求帶電粒子在加速器中運動的總時間.

圖1 圖2

解析分析帶電粒子加速的全過程，可簡化為加速-偏轉-加速-偏轉…，反復運動，仔細分析其特征：1. 洛倫茲力不做功，不影響速率的變化，當然也起不到加速的效果.2. 在電場中的加速運動是一個勻加速的過程且每次的位移均為d. 3. 從時間累積來看，每一段在磁場中的運動都是經歷了半個周期；若將電場中的運動連接起來，就是一個初速為零，總位移為Nd的勻加速直線運動(其中N為通過電場的次數——加速的次數)，分析和分解到此，情景就十分清晰了.最大速度設為v，

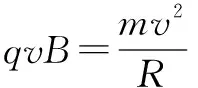
每次經電場加速增加的動能為ΔEk=qUm

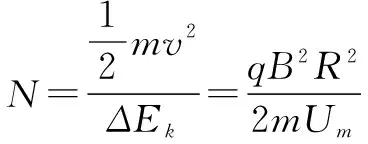
在磁場中運動的總時間：

在電場中運動的總時間：

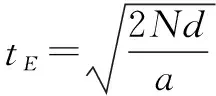
所以所加交變電場的周期也應作相應的調整，對于現代技術而言完全不是問題，可利用計算機直接控制.

其實，在空間不受限制的情況下，討論帶電粒子在交變的組合場中運動的位置；路程等空間量時，此法同樣可用.

例2在光滑絕緣的水平桌面上建立一xOy坐標系，平面處在周期性變化的電場和磁場中， 電場和磁場的變化規律如圖3所示(規定沿+y方向為電場強度的正方向，豎直向下為磁感應強度的正方向).在t=0時刻，一質量為10 g、電荷量為0.1c且不計重力的帶電金屬小球自坐標原點O處，以v0=2 m/s的速度沿x軸正方向射出.已知E0=0.2 N/C、B0=0.2πT.求：(2n-1)s～2ns(n=1,2,3,…)內金屬小球運動至離x軸最遠點的位置坐標.

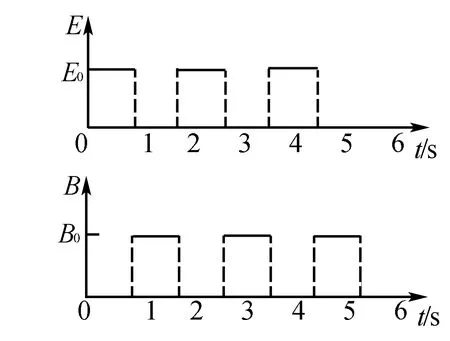
圖3

首先需計算在磁場中運動的周期

帶電粒子的運動情形已然明了，先作類平拋運動1 s，接著作勻速圓周運動，完成一周回到圓周運動的起點，繼續沿原拋物線運動1 s，再作勻速圓周運動…如此反復進行.“合并同類項”，則可將整個運動分別當作是連續的類平拋運動和在不同位置以不同速率進行的勻速圓周運動.

對于復雜運動我們通常采用運動的分解并抓住分運動的獨立性和同時性進行處理，同樣可以采取“先分割再整合”的方式進行求解，在考慮各段的獨立性的同時，要特別重視交界處的特征物理量——聯系兩個過程的物理量，如以上兩例中的交界處的瞬時速度和過程中速度的偏向角等.在(2n-1)s前已剛好在電場中運動n(s)

此時x=v0t=2n(m)，vx=v0=2 m/s

距離x軸最遠時，即圓周此處的切線與x軸平行.

在磁場中運動的速度的偏向角φ2與電場中運動的速度的偏向角φ1的關系為

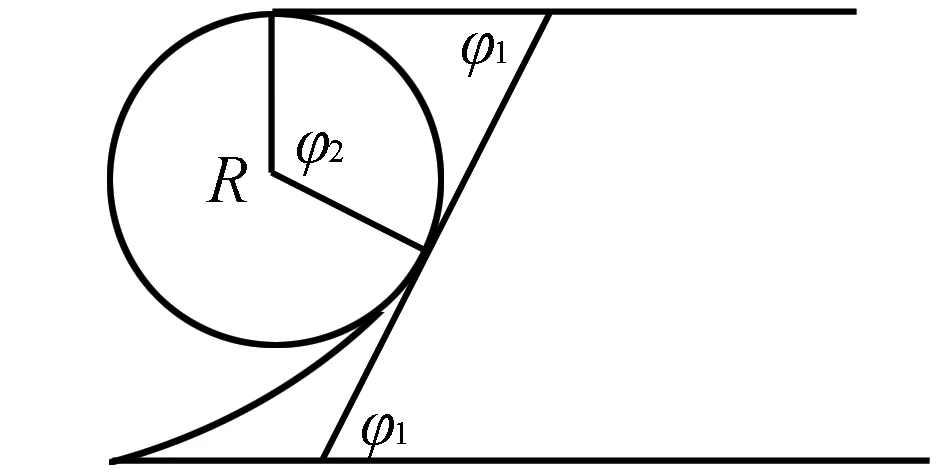
圖4

φ1+φ2=π

ym=y+R(1+cosφ1)

xm=x-R*sinφ1

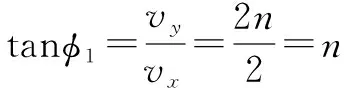
事物都是相互聯系的，當我們在研討物理問題時，遇到無法建立物理模型或者找不到突擊方向等難題，可以從自然界、生活中或者其他學科中尋找借鑒和啟發.