2020年全國高考數學一卷(理)20題解法賞析

陳志年

(安徽省合肥市肥西中學 231200)

2020年全國高考數學一卷(理)20題是一道解析幾何題，其中第二問是證明直線過定點.雖然是一類常見常考的題型，但是解決起來有一定的難度.難點在于：引進一個參數，思路簡單，可運算量大，要求運算流暢、準確；引進多個參數，最后涉及到參數的消去與保留，要求思維靈活、縝密.下面給出該題的多種解法及評析，欣賞一題多解的妙趣；領略難點突破的秘訣.

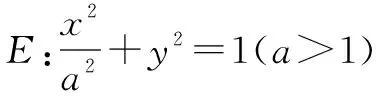
(1)求E的方程；(2)證明：直線CD過定點.

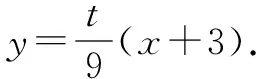
評析本解法兩次將直線方程代入橢圓方程得到關于x的一元二次方程,有一定的運算量，要求零失誤;利用韋達定理求得C、D的坐標，是一個技巧;寫出直線CD的方程還需要化簡整理，方能得到所要證的結論.

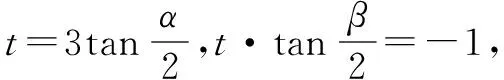
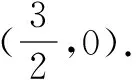
評析本解法利用橢圓的參數方程設點的坐標，減少了參數的個數；整個解答過程中，利用了多個三角公式，如：同角三角函數基本關系公式，兩角和與差公式，二倍角公式及通過角的變換推導的“和差化積”公式等，可以說三角公式的運用得到了極致.

解法3由(1)知A(-3,0),B(3,0).設P(6,t)，根據對稱性直線CD所過定點在x軸上.

消去m得 -(n2-9)(y1+y2)+3n(n-3)y1-n(n+3)y2=0，

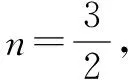
當t=0時，直線CD的方程為y=0.

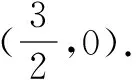
根據對稱性直線CD所過定點在x軸上.

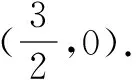
評析本解法引進更多的參數，利用C、D在橢圓上，我們首先消去y1和y2，得到4x1x2-15(x1+x2)+36=0，至此應用韋達定理解答顯而易見，水到渠成.解析幾何中，設而不求、加強韋達定理的應用是解答問題的重要方法.