聚焦核心素養下導數教學的思考

陳 剛

(江蘇省蘇州市昆山經濟技術開發區高級中學 215300)

一、新教材人教A版選修二中導數的相關知識

1.導數概念及其意義

(1)通過實例分析，經歷由平均變化率過渡到瞬時變化率的過程，了解導數概念的實際背景，知道導數是關于瞬時變化率的數學表達，體會導數的內涵與思想;

(2)體會極限思想;

(3)通過函數圖象直觀理解導數的幾何意義.

2.導數運算

(2)能利用給出的基本初等函數的導數公式和導數的四則運算法則，求簡單函數的導數，能求簡單的復合函數(限于形如f(ax+b))的導數;

(3)會使用導數公式表.

3.導數在研究函數中的應用

(1)結合實例，借助幾何直觀了解函數的單調性與導數的關系，能利用導數研究函數的單調性；對于多項式函數，能求不超過三次的多項式函數的單調區間；

(2)借助函數的圖象，了解函數在某點取得極值的必要條件和充分條件；能利用導數求某些函數的極大值、極小值以及給定閉區間上不超過三次的多項式函數的最大值、最小值，體會導數與單調性、極值、最大(小)值的關系.

二、導數在高考中所考查的內容和解題策略

1.導數考查內容和題型的研究

從高考對導數的要求看，考查共分為三個層次，一是考查導數公式，求導法則與導數的幾何意義；二是導數的簡單應用，包括求函數的單調區間、極值、最值等；三是綜合考查，如研究函數零點、證明不等式、恒成立問題、求參數范圍、極值點偏移等.

高考導數在壓軸題和小題中都有考查，難度控制在中等以上.復習時應特別注意將導數內容與傳統內容中有關不等式、數列、函數圖象及函數單調性有機結合，設計綜合題，考查學生靈活應用數學知識分析問題、解決問題的能力.

例1(2020年新高考全國Ⅰ卷)已知函數f(x)=aex-1-lnx+lna．

(1)當a=e時，求曲線y=f(x)在點(1，f(1))處的切線與兩坐標軸圍成的三角形的面積；

(2)若f(x)≥1，求a的取值范圍．

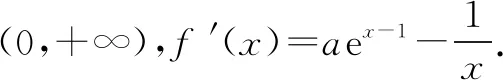
(1)當a=e時，f(x)=ex-lnx+1，f′(1)=e-1.

求得切線方程為y=(e-1)x+2．

(2)按01分類求解.

最終可得，a的取值范圍是[1,+∞)．

注：本題具體指向學生的數學運算、數學建模、邏輯推理三大核心素養，第(1)問考查導數幾何意義，第(2)問利用導數研究不等式恒成立問題，考查綜合分析求解能力，分類討論思想和等價轉化思想.

面對高考中的導數題常考常新，我們能夠做到的就是備考面能夠全覆蓋，如導數幾何意義的應用、單調性問題、極(最)值問題、零點問題、不等式的證明、參數范圍的確定的等.

2.導數常規考點及復習建議或解題策略

考點1：函數單調性，極值，最值的直接應用

(1)導數中不含參數：步驟求定義域，求導，求極值點，列表，求極(最)值.

復習建議：第一問一定要穩.導函數不能求錯，否則整個題目會一并掛掉.要求求導時記牢導數公式不要圖快，小心謹慎.

(2)導數中含參數：涉及分類討論，明確分類討論的標準.導數中含參數討論問題更多是與ex及lnx結合，含分子二次函數型(參考定義域)，因式分解型，二次求導型，單根單調型.

例2 已知函數f(x)=alnx+x2(a≠0)，討論函數f(x)的單調性.

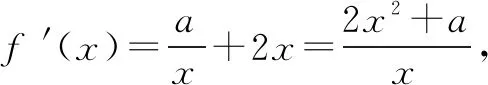
①當a>0時，f′(x)>0，f(x)在(0，+∞)上遞增．

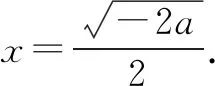
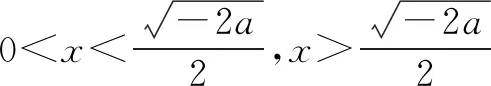
復習建議：備考時我們應該對含參數討論單調性求極值最值這樣的知識點練習到位，爭取在導數的第一問上拿到滿分.

考點2：不等式恒成立問題

這類問題一般都設置在導數題的第二問，屬于有一定難度的問題.需要學生有一定的綜合能力，不僅對導數要有較深刻的理解，而且對于不等式、函數等知識要有比較好的掌握.

解題策略(1)分離變量求最值——分離時要特別關注是否需要分類討論，分類要結合條件看，不能忽略大前提.要理解清楚分離后求函數的最大值還是最小值；

(2)構造函數求最值——如f(x)>g(x)恒成立，就是將上述的函數轉化為了另一個函數，并沒有本質的區別；

(3)試根法——有效點縮小參數范圍是關鍵點.

例3 已知函數f(x)=alnx+x2(a≠0).

(1)當b=2時，討論函數f(x)的單調性；

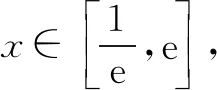
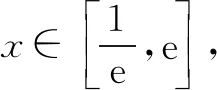
注：(1) 研究含參數的函數的單調性，要根據參數對不等式解集的影響進行分類討論，如：開口方向、是否有解、解是否在定義域的取值范圍內、解之間的大小等；

(2) 劃分函數的單調區間時，還要確定導數為0的點和函數的間斷點．

(3) 個別導數為0的點不影響所在區間的單調性.

考點3：交點與根的分布

類型1.函數f(x)與g(x)(或與x軸的交點)——方程根的個數問題；兩個函數的圖象有交點也就是方程組有解，但是對于超越函數我們往往解不出，那么轉化為一個函數，再利用圖象研究其極值和最值成為了一種思路；

類型2.切線的條數問題——以切點的橫坐標為未知數的方程的根的個數；

類型3.極值點個數問題——導函數為0時根的個數(注意表格檢驗);

考點4.已知函數在某個區間上的單調性求參數的取值范圍.

解題策略(1)導函數在給定區間上的恒成立問題，然后回歸基礎題型，可采用分離參數法、構造函數法、分類討論等方法；

(2)子集思想，即所給區間是函數單調區間的子集.

考點5：不等式的證明

解題策略(1)構造函數

(2)放縮法

第一部分：對數式放縮

放縮成一次函數：lnx≤x-1;lnx

放縮成二次函數：lnx≤x2-x；

放縮成反比例函數：lnx>1-1/x.

第二部分：指數式放縮

ex>x>lnx，ex≥x+1，ex≥ex.

第三部分：三角函數式放縮

sinx

三、導數在教學中建議

1.立足課標，激活教材

課本是教學之本，重視教材上一些基礎知識的形成過程，加強對教材例、習題的研究與再創造；

2.注重能力，培養素養

理解導數的基本概念；加強對邏輯推理能力和數學運算能力的培養；多滲透化歸與轉化思想；

3.關注題型，抓住特征

三角函數，指數函數，對數函數，多項式函數，分數函數，以及幾種函數的相互融合；

4.關注熱點，明確趨勢

函數的單調性、極值和最值，函數的零點(隱形零點)，極值偏移問題，證明函數不等式(幾何背景)，不等式的恒成立問題，比較大小，解決實際問題等等.