Excel在高校數學教學中的應用

劉昕輝，鞏曉秋

(遼陽職業技術學院現代教育技術中心，遼寧遼陽111000)

0 引言

隨著社會的不斷發展，信息技術、虛擬技術等在教育領域的應用逐漸普及，高校的教學也發生了重大的變革，教育信息化、智能化發展已成為一種趨勢.充分利用信息技術手段，可以為教育賦能，給學習者帶來全新感受[1].

Excel是一款常用的辦公自動化軟件，該軟件不僅操作簡單，而且功能十分強大，被廣泛應用于金融、財務管理等領域中.Excel除了具有常用函數功能，還具有很多專業的數學函數功能，如log(n，base)、power(x，n)、minverse(array) 等等，以及強大的數學公式編輯器及規劃求解等功能，這些功能既能夠完成大部分數學運算，也能夠滿足數學教學的需要.相對于其他專業化的教學輔助軟件，如幾何畫板、IMatlab等，Excel可謂是一個簡單且高效的工具，它不需要用戶編程即可實現對數據的分析與計算.在高校數學教學中，巧妙應用Excel可以快速、準確、直觀地解決很多數學難題，優化數學教學手段.下面結合具體問題探討Excel 在高校數學教學中的應用.

1 利用Excel 繪制復雜函數曲線

例 在同一坐標系中繪制函數f(x)=ex-sinxcosx與y=ln(x2+1)cosx的曲線.

在高校數學教學中，常常利用幾何畫板來繪制函數曲線，繪圖過程有時過于繁瑣，其靈活性和高效性并不能滿足高校數學教學的實際需要.而使用Excel中強大的數學公式、豐富的內置函數及便捷的圖表功能，可以方便、快速、準確地得到所需的相關數據并將其繪制成對應的函數圖像曲線，同時還可以根據需要將繪制的多個函數曲線放在同一坐標系中進行比較，使學生在快速、直觀地獲得函數曲線的同時，加深對函數圖像及性質的理解，大大提高了高校數學教學的精確度和實效性.繪制步驟如下：

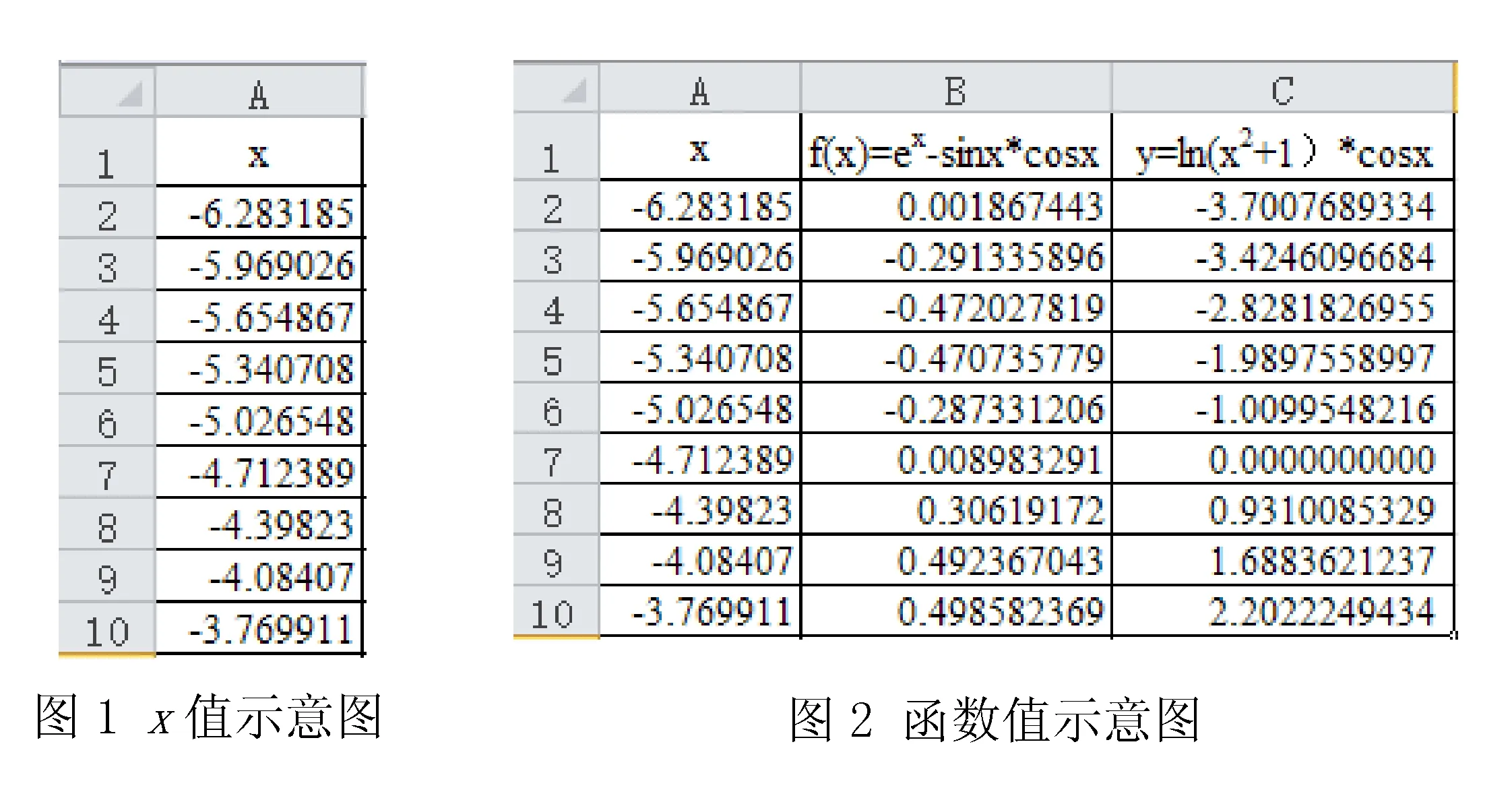
(2)計算函數值.在B2和C2單元格中分別輸入公式“=exp(A2)-sin(A2)*cos(A2)”和“=ln(A2*A2+1)*sin(A2)”.然后選中B2單元格，雙擊該單元格右下角的自動填充柄，以自動填充方式計算與 A列數據相對應的第一組函數值，并將計算結果填充至B3∶B42單元格.按照同樣的方法得到第二組函數值，并自動填充到C3∶C42 單元格中，如圖2所示.

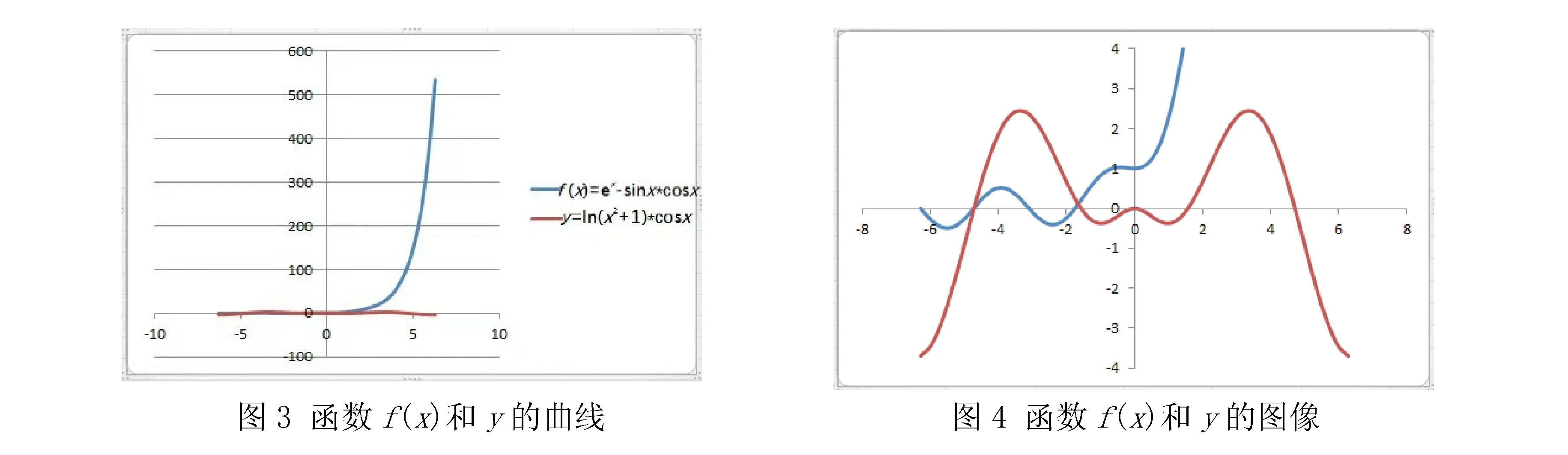
(3)根據前面得到的數據生成函數曲線.單擊A2∶C42的任一單元格，單擊“ 插入”選項卡 ，在其中的“圖表” 功能區中選擇“散點圖”中的“帶平滑線的散點圖”，可以在同一張圖表中同時得到兩個函數的曲線，如圖3所示.單擊圖表右側的圖例，按Delete鍵將其刪除.

(4)設置坐標軸刻度.右鍵單擊縱坐標軸，彈出快捷菜單，選擇“設置坐標軸格式”.打開“設置坐標軸格式” 對話框 ，將“最小值”“最大值”“主要刻度單位”均設置為“固定”，數值分別為“-8”“8”和“1”.根據需要選擇“布局”選項卡中的“坐標軸”功能區中的“網格線”，將坐標系中的主要網格線刪除，得到函數圖像，如圖4所示[2].

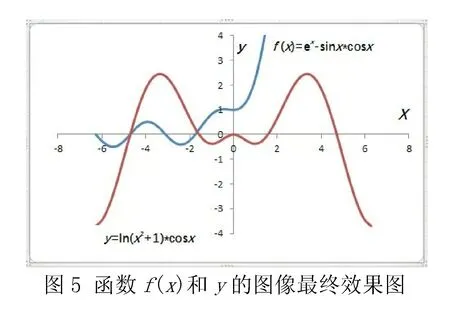
(5)標注函數解析式和坐標軸標題.單擊“ 插入”選項卡，在“文本 ”區中選擇“文本框”中的“橫排文本框” ，在函數圖像旁拖出一個文本框，在文本框中輸入第一個函數解析式“f(x)=ex-sinx*cosx”，適當調整文字的字體、大小及位置，按照同樣方法再為另一個函數的圖像添加解析式“y=ln(x2+1)*cosx”.接下來，單擊“ 布局”選項卡，在“標簽 ”功能區中選擇“坐標軸”中的“ 主要橫坐標軸標題 ”，在標題文本框中輸入“x”，適當調整文字大小及位置，再用同樣的方法標注縱坐標軸標題，最終完成圖像的繪制，如圖5所示.

2 利用Excel求復雜方程的近似解

例 求三次方程 2x3+x2+0.8x-2.1=0在(0,1)之間的一個近似解.

這是一個三次方程，不能利用分解因式的方法求其根，此時利用Excel可以輕松求出該方程的近似解，步驟如下：

(1)分別在A2 和A3單元格中輸入0和0.01，然后將A2和A3單元格同時選中，拖動鼠標至單元格A102，這樣就得到了一組自變量x的值0，0.01，0.02，…，1，如圖6所示.

(2)單擊B2單元格，輸入公式“=2*power(A2,3)+ power (A2,2)+0.8*A2-2.1”，此時計算出x=0時方程左邊式子的值.雙擊B2單元格右下角填充柄，自動計算每個x所對應的函數值并填充至單元格B102，如圖7所示.從得到的函數值中可以看出方程的根介于0.76～0.77之間，如圖8所示.

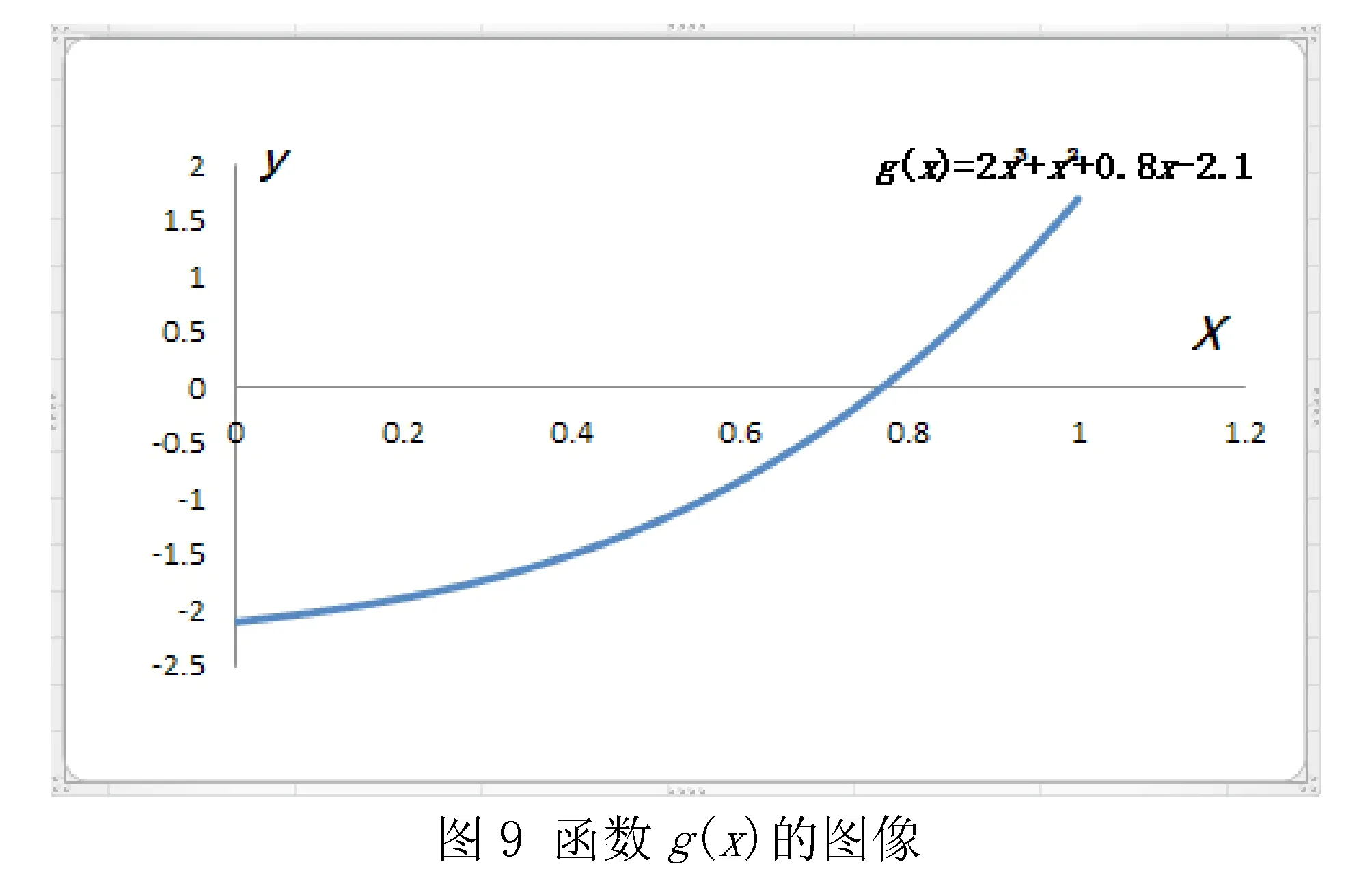
(3)為了讓學生更加直觀地了解方程近似解的情況，可以按照前面敘述的方法繪制函數g(x)= 2x3+x2+0.8x-2.1=0的圖像，如圖9所示.通過圖像可以清楚看出函數g(x)在區間(0，1)之間的取值變化規律及方程的根.

3 結語

巧妙應用Excel所提供的強大功能，可以輕松解決高校數學教學過程中用常規方法無法解決的問題，提高高校數學教學的精確度和效率，豐富教學課件的類型，提高課件的靈活性和課堂教學的實效性，同時也有利于提高學生數學學習能力和利用計算機解決實際問題的能力.