課程安排中的匹配問題及求解

張敏捷

（湖北文理學(xué)院數(shù)學(xué)與統(tǒng)計學(xué)學(xué)院 湖北·襄陽 441053）

為保障教學(xué)質(zhì)量，各級各類的學(xué)校都要結(jié)合自己的師資力量，合理地安排教學(xué)，盡最大的努力讓學(xué)生受到最好的教育。因此，在現(xiàn)有師資條件下，如何合理地安排教師進行課程教學(xué)，具有重要的研究意義。

例如，某學(xué)校某教學(xué)部，要安排n位教師負責n門課程的教學(xué)工作。為盡量減輕教師的教學(xué)負擔，要求每位教師負責一門課程的教學(xué)工作。如何安排可以達到最好的教學(xué)效果？

將每位老師和每門課分別用一個點表示，若某位教師能承擔某門課程的教學(xué)，則將對應(yīng)的兩個點連邊。同時可基于各位老師以往負責各門課程的教學(xué)效果，對這些邊進行賦權(quán)。為方便討論，不妨先假設(shè)每位教師都有承擔這n門課程教學(xué)的能力。此時，可得到2n個頂點的賦權(quán)完全二部圖，而此時課程安排問題便可以看作求賦權(quán)完全二部圖的最大完美匹配問題。

例：某校某學(xué)期要安排五位教師甲、乙、丙、丁、戊承擔五門課程的教學(xué)任務(wù)。根據(jù)近五年的學(xué)生評教，統(tǒng)計出各位教師負責相關(guān)課程的平均成績，如下表所示。若以此為依據(jù)安排教學(xué)任務(wù)，如何安排，可使教學(xué)質(zhì)量最好？（假設(shè)每位教師負責一門課程的教學(xué)任務(wù)。）

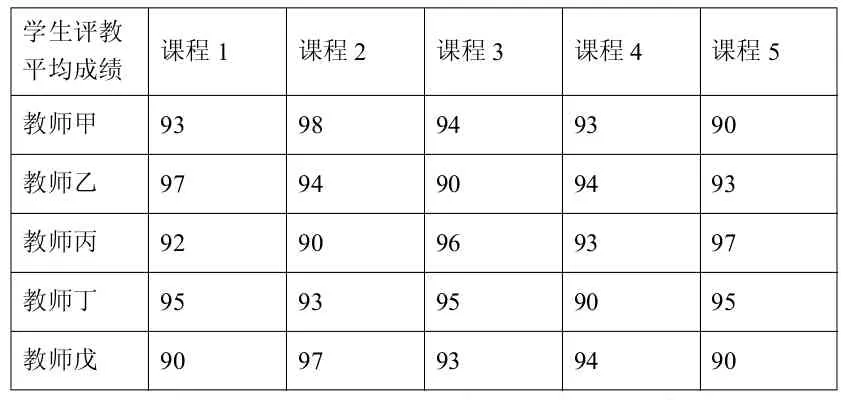
學(xué)生評教平均成績 課程1 課程2 課程3 課程4 課程5教師甲 93 98 94 93 90教師乙 97 94 90 94 93教師丙 92 90 96 93 97教師丁 95 93 95 90 95教師戊 90 97 93 94 90

解：首先，將此問題轉(zhuǎn)化為最小完美匹配問題。寫出此問題對應(yīng)的效益矩陣A，

注意到矩陣A中最大元是98。分別用98減去矩陣A中各元素，得到矩陣C。不難驗證，求解以A為效益矩陣的最大完美匹配問題等同于求解以C為效益矩陣的最小完美匹配問題。

事實上，我們可以先將矩陣C的各行各列減去相應(yīng)的最小元素，即

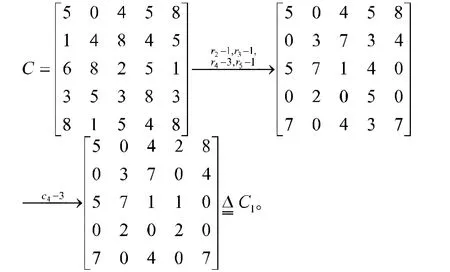
因此，我們可以得到如下最優(yōu)方案：教師甲負責課程2，教師乙負責課程1，教師丙負責課程5，教師丁負責課程3，教師戊負責課程4。此時總評教成績?yōu)椋?8+97+97+95+94=481。

以上，我們將課程安排問題轉(zhuǎn)化為了二部圖的最大完美匹配問題，并利用匈牙利法對其進行了具體的求解。下面，我們給出關(guān)于此問題的幾點思考與推廣：

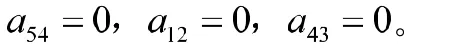
（2）按照上述方法尋找“0”時，若在某一步發(fā)現(xiàn)對應(yīng)的矩陣中含“0”最少的行或列至少含有2個“0”，則說明最優(yōu)方案并不唯一。我們不妨將上述例題中的數(shù)據(jù)稍作修改：將教師丁負責課程3的學(xué)生評教平均成績由之前的“95”改為“94”。重復(fù)上述過程可得

此時，我們就會自然而然地考慮：到底有多少個最優(yōu)方案呢？通過上述過程，不難發(fā)現(xiàn)，確定最優(yōu)方案的個數(shù)等同于尋找矩陣中位于不同行、不同列的5個“0”的組數(shù)。而這個問題又可以轉(zhuǎn)化為求其補矩陣的積和式的問題。在文獻[3]中，鐘守楠教授和高成修教授給出了矩陣的補矩陣及其積和式的定義：

定義1：將矩陣M中“0”改為“1”，非零元都改為“1”，所得矩陣稱為M的補矩陣。

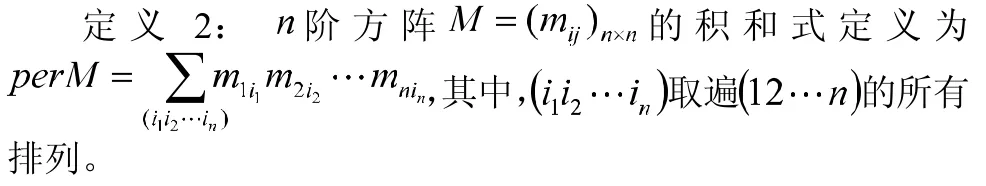
由定義2發(fā)現(xiàn)，方陣積和式的定義與方陣行列式的定義極為相似，只是在各項前面不用考慮正負號了而已。因此，計算矩陣積和式最有效的方法便是利用行列式計算中按行（列）展開的思想進行的，我們也通常通過按某一行（列）展開來計算方陣的積和式，只需注意展開時需要考慮該行各元素乘以對應(yīng)的余子式之和，而不是代數(shù)余子式。

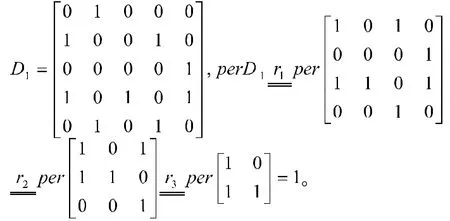
（1）值得注意的是，對于效益矩陣或C者經(jīng)過上述變形后的效益矩陣，如果其補矩陣的積和式為0，并不能說明這個問題沒有最優(yōu)方案。站在枚舉的角度思考，此問題等同于在5種可能的方案里面找最優(yōu)方案，故最優(yōu)方案是一定存在的。

我們可以采用如下方法：

不妨在上述例題中，將教師丙負責課程2與課程5的學(xué)生評教平均成績對調(diào)，即教師丙負責課程1-5的學(xué)生評教平均成績分別為 92，97，96，93，90。重復(fù)上述過程可得：

（2）此問題可考慮借助于Lindo或者Lingo程序來求解。尤其是當教師的人數(shù)與課程的門數(shù)不相等的情形。具體解決思路值得進一步研究。

致謝：

感謝國家自然科學(xué)青年基金（No.11901179）的資助；感謝湖北文理學(xué)院科研啟動基金的資助。