從有限到無限，逐步感知極限思想

鮑慶賀

[摘 要]極限思想是小學常見的數學思想之一，蘊含于許多知識之中，但極限思想卻是學生最難以理解的思想之一。在教學“圓的面積”過程中，教師應層層深入，化抽象為直觀，從有限到無限，讓學生逐步感知極限的存在，并充分借助可以直觀化的教學工具展示教學過程，提升學生對極限思想的認識。

[關鍵詞]極限思想;圓的面積;幾何畫板

[中圖分類號] G623.5[文獻標識碼] A[文章編號] 1007-9068（2021）02-0062-02

在一次借班上課前，知道了要上“圓的面積”這一課，一位學生便問道：“要帶圓規嗎？”我答：“不需要。”學生聽到后十分詫異，可見，他們已經根深蒂固地將圓列為一個“特殊對象”了，根本不可能把“圓”與“方”扯到一起。如何打破這種想法？何不從圓與方之間的關系入手，讓學生感受到“圓”與他們認識的“方”之間的關系？

一、感知圓與方的聯系，在想象中感受無限的存在

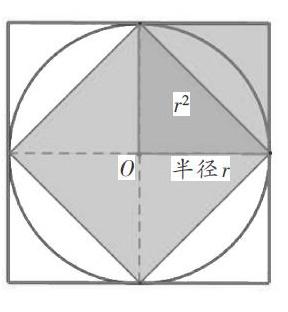
要求圓的面積，就必須將圓轉化成長方形、平行四邊形等基本圖形。如何設計教學才能讓學生自然而然地感受到圓與方之間存在聯系呢？我從圓與邊長為圓的半徑的正方形的面積出發。

師：這里有一個圓，如果以它的圓心為一個頂點，以它的半徑為邊長畫一個正方形。你知道正方形的面積嗎？（半徑為r）

生1：半徑乘半徑。

生2：可以直接說成r2。

師：接著畫3個這樣的圖形，得到一個大的正方形，它的面積是多少？

生3：4×r2。

師：在圓內也可以畫一個最大的正方形，你知道它的面積嗎？

生4：大正方形的面積是4r2，把它平均分成8份，這個小正方形剛好占了4分，是它的一半。……