抽樣不滿足時的混疊現象仿真



摘要:對一個二維帶限函數抽樣,并通過分析抽樣間隔和改變參數,驗證欠采樣、濾波后的頻譜混疊現象,借助Matlab對信號時域與頻域的多幅2D和3D圖像進行繪制和分析,有助于更直觀深入理解抽樣定理與抽樣不當引起的頻譜混疊和信號失真現象。
關鍵詞:抽樣定理,欠采樣,混疊,失真
1 引言
“抽樣定理”是信號與系統課程中頻域分析時一個重要知識點,是模擬信號向數字信號轉換的一個關鍵性定理。“抽樣間隔”是該定理的核心內容。本文利用Matlab作為分析和作圖工具,選取某帶限函數,通過選擇樣間隔,得到抽樣后的函數頻譜,頻域濾波后,觀察欠采樣和頻譜混疊現象,來更直觀的理解抽樣定理。
2 抽樣定理
香農抽樣定理指出,對于能量有限的帶限信號,要實現信號的無失真恢復,采樣頻率必須不小于信號帶寬的兩倍,即。當抽樣定理不滿足,即時,則頻譜將產生混疊,不能正確恢復原始信號。本文通過分析抽樣間隔,來驗證抽樣間隔選擇不當而出現欠采樣和混頻現象,無法正確復原原函數的情況。利用直觀的仿真圖形,進一步闡明抽樣定理的內涵,通過混頻現象的仿真,加深概念及定理的理解。
3 仿真驗證
3.1抽樣信號的恢復
對一個二維帶限函數用矩形點陣列抽樣,則抽樣函數定義為:
其中comb為梳狀函數,用函數陣列給出,X,Y是陣列沿x和y方向上的間隔。
由(1)式可得的頻譜形式為:
其中u,v為頻域坐標,分別對應于空域x,y坐標。符號為卷積,為傅里葉變換。
假設函數是帶限函數,其頻譜如圖1所示,其頻譜只在頻率空間的有限區域R上不為零。該函數被抽樣后,抽樣函數的頻譜不為零的區域根據(2)式,可由在頻率平面的每一個點的周圍劃出R區域得到。如果和足夠小,則和的間隔就會足夠大,以保證相鄰區域不重疊。的頻譜如圖2所示。
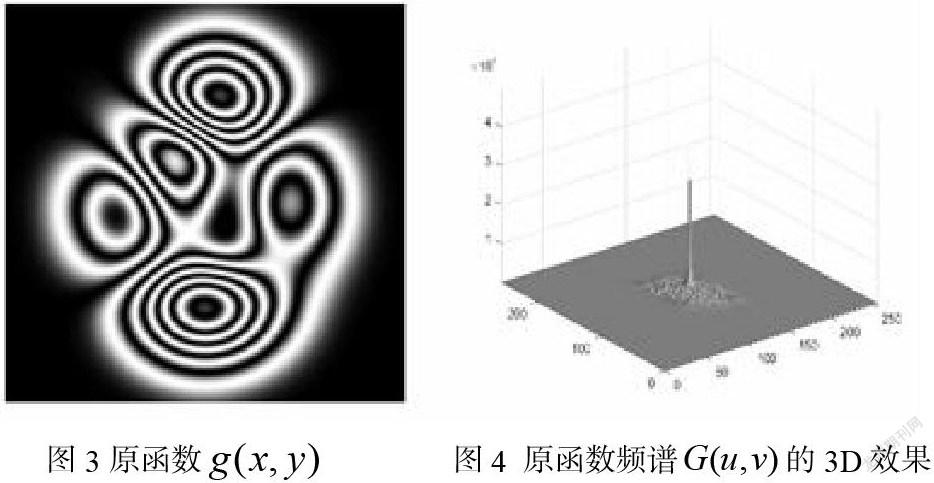
由抽樣定理,令2Bx和2By分別表示完全圍住區域R的最小矩形沿u和v方向上的寬度,則空域抽樣點陣間隔滿足,條件時,可保證頻譜區域分開而不混疊,原函數可恢復。反之,將出現頻譜混疊,無法正確恢復原函數。仿真中,利用Matlab編寫m文件實現,使用自帶的peaks函數生成一個二維帶限函數作為這里的,其數學表達式形式記為:,該函數的空域圖形如圖3,其頻譜3D效果如圖4。
從圖4可知,所選帶限函數沿u,v方向帶寬都小于128個像素,由于圖像大小為256*256,根據抽樣定理,重構原函數的條件是抽樣間隔至少滿足Y=256/128=2個像素,因此這里可選擇X=Y=2。
為觀察欠采樣和混疊現象,選擇4個像素為抽樣點陣間隔,顯然不再滿足抽樣定理,出現欠采樣。此時對按照對應于2個像素間隔的128*128濾波器進行頻譜濾波,再傅里葉逆變換,則可看到濾波后頻譜與復原函數分別如圖5和6。由于出現欠采樣且濾波器選擇為128*128像素,可看出恢復的函數頻譜已明顯混頻,復原的函數出現了嚴重失真。
4 結論
由以上仿真可看出,對于二維連續函數,當選擇采樣間隔不滿足抽樣定理要求時,使用相應濾波器頻譜濾波后,原函數頻譜明顯混疊,導致復原的帶限函數嚴重失真,由此可看出抽樣間隔和頻率濾波的重要性。此外,通過多幅2D和3D圖像,更直觀表述了抽樣定理的內涵,有助于對該定理深入理解。
參考文獻
[1]魏坤,余秋菊.信號與系統中基于抽樣定理的教學內容總結與分析[J].教育教學論壇,2019(34):255-256.
[2]張幗奮.抽樣分布的若干反例[J].數學學習與研究,2019(08):9+11.
[3]丁俊,夏太珊,劉倫杰,楊露,袁莉,張文.基于MATLAB的抽樣定理仿真研究[J].通信與信息技術,2018(03):71-72+61.
作者簡介:吳云飛(1980—),女,重慶人,碩士,講師,研究方向為計算機應用技術、電氣工程及其自動化。

