借助構造法 打破圓錐曲線“藩籬”
宋德銀
(江蘇省泰州中學 225300)
在圓錐曲線類型的題目中,構造法能很好地發(fā)揮學生的創(chuàng)造性思維.在應用構造法解決圓錐曲線時,我們要善于結合題目要求以及自身聯(lián)想構造出滿足條件的數(shù)學對象,使圓錐曲線題型的解法突破常規(guī),另辟蹊徑.
一、構造不等式求解參數(shù)范圍
探求圓錐曲線中的參數(shù)取值范圍是近幾年高考考查的熱點與難點,學生要善于深入題目條件,挖掘題中的隱含信息構建與參數(shù)有關的不等式或者不等式組,將題目所求問題轉(zhuǎn)化為求解不等式或不等式組的問題.

(1)求橢圓C的標準方程;
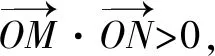
分析(1)當線段MN為長軸時,長度最長,4=2a,a=2,可得橢圓C的標準方程;(2)直線MN的斜率存在且不為0,設方程為y=kx+2,將其與橢圓的方程聯(lián)立可得(1+4k2)x2+16kx+12=0,由Δ>0來構造不等式,并求解不等式,結合韋達定理求出直線OP斜率的取值范圍.
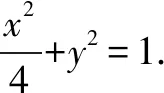

二、構造方程求解最值問題
對于圓錐曲線這類復雜的數(shù)學題,往往會出現(xiàn)自變量與因變量的概念,因此我們可以根據(jù)需要結合有利的數(shù)學條件來進行思路框架的設計.針對題目的未知參數(shù),將有關的條件構成方程組,通過解方程組最終確定最值或是確定范圍.
例3已知動圓C過點P(0,4),且在x軸上截得的弦長為8.
(1)求動圓的圓心C的軌跡方程;

分析(1)設圓心C的坐標,及圓與x軸的其中一個交點M,由橢圓可得C的坐標之間的關系,即求出動圓C的軌跡方程;
(2)設A,B,Q的坐標,求直線AB的方程并與橢圓方程聯(lián)立,構造方程組,求出兩根之和及兩根之積,由題意得|AD||BD|的表達式,由Q的坐標的范圍求出其最大值.
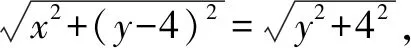
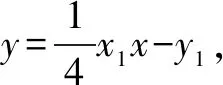
構造法善于利用題目的有利條件,將難以直接解決的參數(shù)問題轉(zhuǎn)化到方程或函數(shù)等數(shù)學問題上來,便于學生理解,也能提高學生的解題效率.應用構造法解決圓錐曲線的問題,有助于學生理解圓錐曲線的實際應用.

