不一般的相似
——圓錐曲線中的位似關系
2021-01-12 07:08:28陳峰
數理化解題研究 2020年34期
關鍵詞:拋物線
陳 峰
(江蘇省蘇州大學附屬中學 215006)
在蘇教版《普通高中課程標準實驗教科書數學選修2-1》課本P74-P75中提出了一個很有意思的問題:嘗試證明離心率相同的圓錐曲線“形狀都相同”.如果上述結論成立,這意味著圓錐曲線中也存在著相似關系,為了弄清這個問題,首先必須引入位似的概念.
一、位似
兩個多邊形不僅相似,而且對應頂點的連線相交于一點,并且對應邊互相平行或位于同一直線上,像這樣的兩個圖形叫做位似圖形(homothetic figures),這個交點叫做位似中心,這時的相似比又稱為位似比.
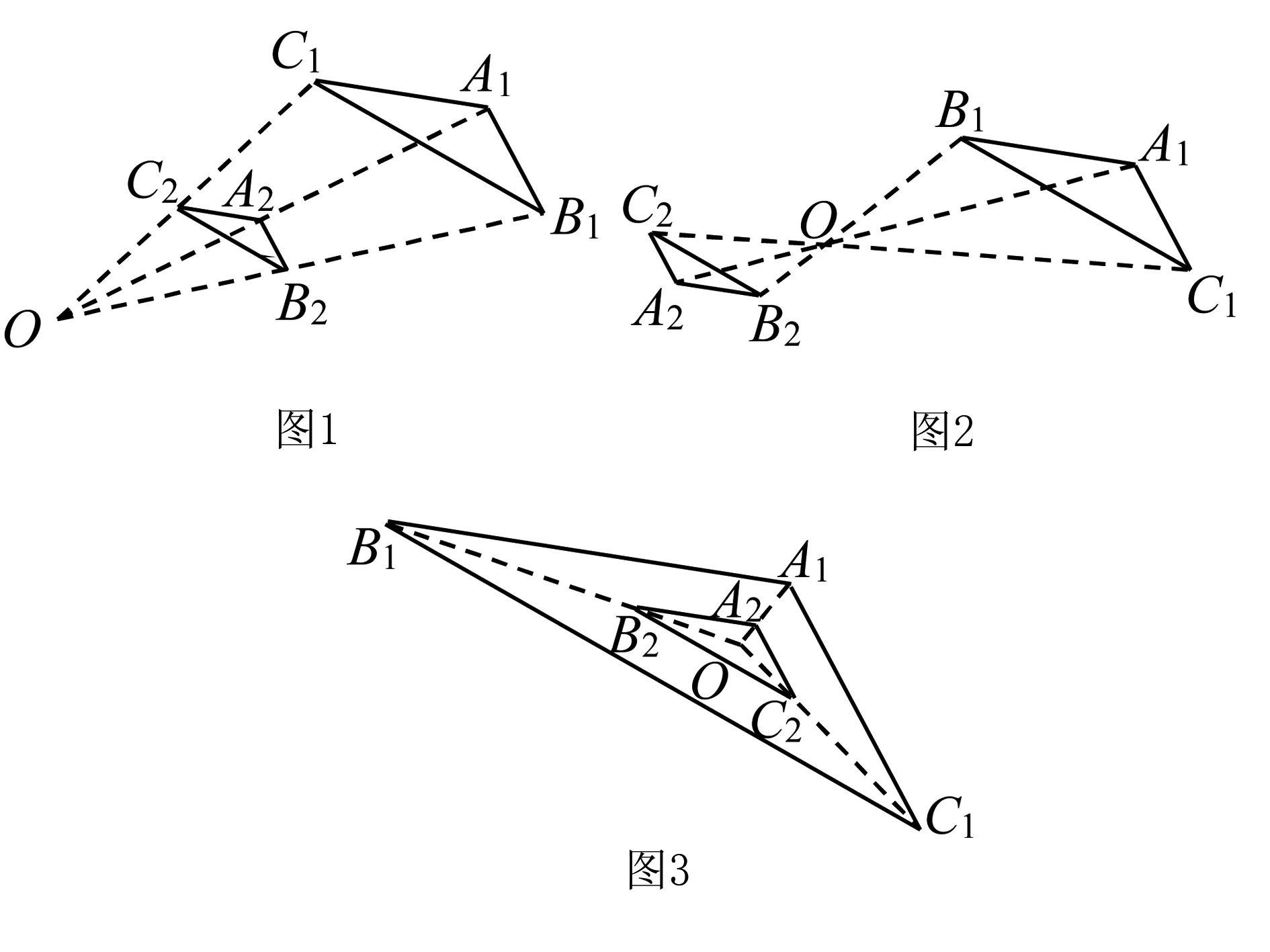
兩個圖形位似,它們的相對位置關系有三種:位似中心在圖形的一側(如圖1)、兩個圖形分居位似中心的兩側(如圖2)、位似中心在兩個圖形的內部(如圖3).
根據位似的定義不難得出:兩個圖形位似則它們一定相似,而兩個圖形相似則它們不一定位似.同時,當兩個圖形位似時,除了滿足相似的一切性質外,還滿足一些特有性質,如“對應頂點的連線相交于一點”、“對應邊互相平行或在同一直線上”等.
二、圓錐曲線的位似關系
1.拋物線
結論1拋物線y=ax2(a>0)與y=Ax2(A>0,A≠a)是位似圖形,原點是位似中心.
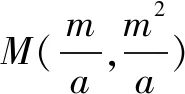
結論2拋物線y=a1x2(a1>0),y=a2x2(a2>0),…,y=anx2(an>0)是位似圖形,原點是位似中心.
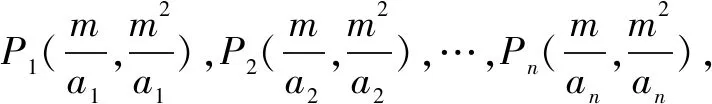
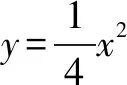
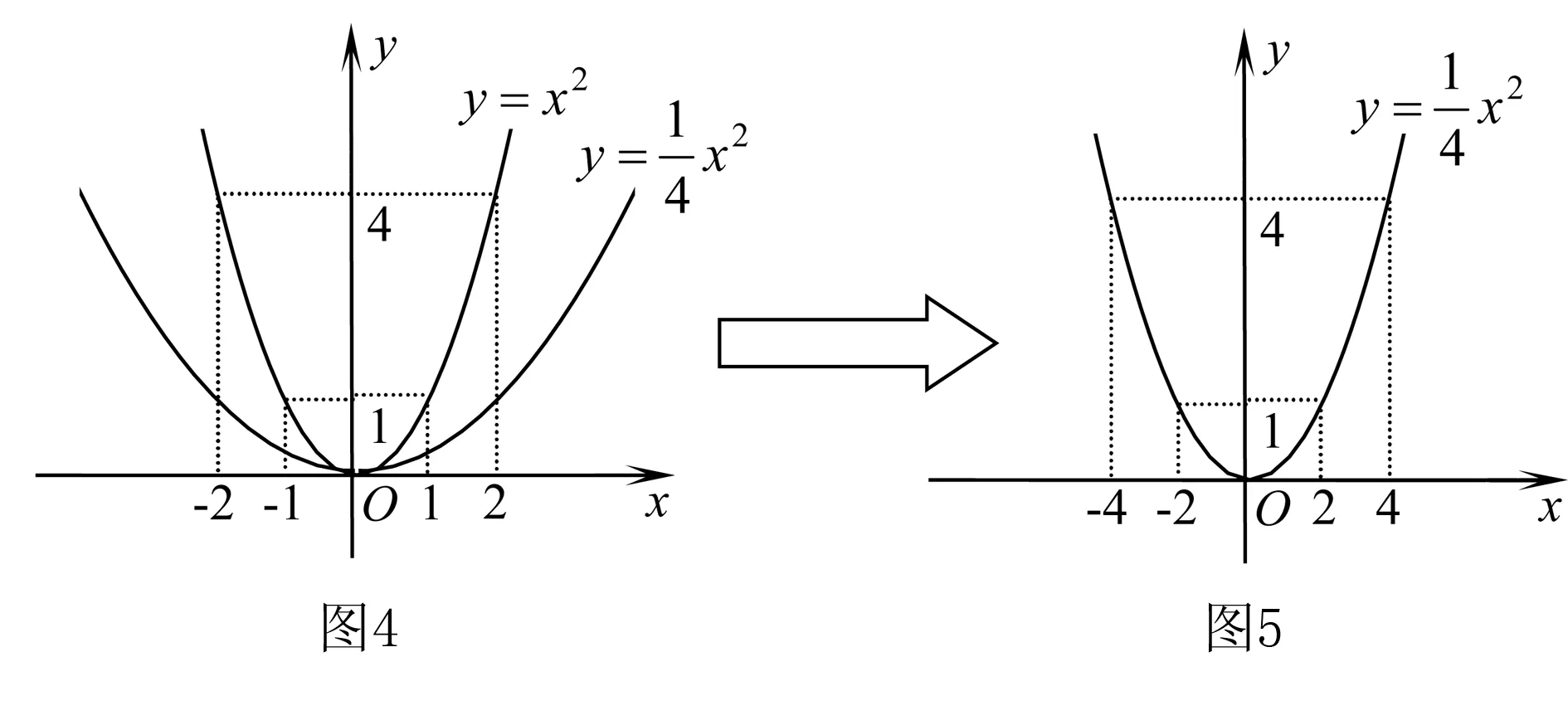

由結論3可知,拋物線的位似中心并不是唯一的,其頂點和焦點均可作為位似中心.
2.橢圓與雙曲線
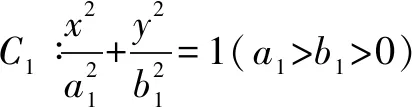
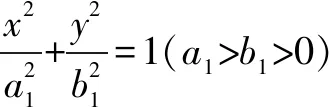
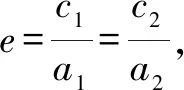
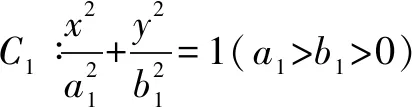
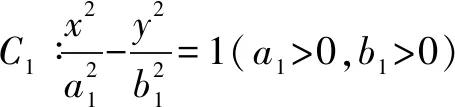

3.圓錐曲線的統一形式

當0
結論6離心率相等的圓錐曲線C1,C2是位似圖形,反之,若圓錐曲線C1,C2是位似圖形,則它們的離心率相等.(證明略)
猜你喜歡
中學生數理化·高二版(2025年2期)2025-03-05 00:00:00
語數外學習·高中版上旬(2024年18期)2024-02-20 00:00:00
中學生數理化(高中版.高二數學)(2022年1期)2022-04-26 13:59:58
中學生數理化(高中版.高二數學)(2022年1期)2022-04-26 13:59:56
中學生數理化·中考版(2021年10期)2021-11-22 07:26:38
中學生數理化(高中版.高二數學)(2021年3期)2021-06-09 06:08:40
中學生數理化(高中版.高二數學)(2021年2期)2021-03-19 08:54:12
中學生數理化·中考版(2019年10期)2019-11-25 09:39:04
中學生數理化·中考版(2018年10期)2018-12-07 00:44:42
中學生數理化·中考版(2017年10期)2017-04-23 06:29:38

