借助變式 活化思維
——高中數(shù)學(xué)中的“變式”應(yīng)用與思考
樊 彪
(廣東省中山市南朗鎮(zhèn)翠亨村中山紀(jì)念中學(xué) 528400)
一、在情境創(chuàng)設(shè)當(dāng)中應(yīng)用變式
良好開始等于成功的一半.教學(xué)期間,數(shù)學(xué)教師需對(duì)導(dǎo)入情境進(jìn)行創(chuàng)設(shè),這樣可以快速吸引高中生注意力,促使其在具體情境當(dāng)中對(duì)問題展開思考以及探究.例如,進(jìn)行“指數(shù)函數(shù)”教學(xué)期間,數(shù)學(xué)教師可設(shè)計(jì)一些活動(dòng),然后設(shè)計(jì)相應(yīng)的變式問題,以此來設(shè)置有關(guān)的教學(xué)情境,激活高中生思維.首先,教師可把一張A4紙平均撕成兩半.之后,把這撕下來的兩個(gè)部分重疊,之后對(duì)折.在此之后,再重疊并且再對(duì)折,一直重復(fù)上邊實(shí)踐過程,如果已知A4紙厚度為0.15毫米.問題一:假設(shè)教師第四次進(jìn)行撕紙之時(shí),同學(xué)們估計(jì)這些紙這時(shí)厚度為多少?問題二:假設(shè)教師第八次進(jìn)行撕紙之時(shí),同學(xué)們估計(jì)這些紙這時(shí)厚度為多少?問題三,假設(shè)教師第十六次進(jìn)行撕紙之時(shí),同學(xué)們估計(jì)這些紙這時(shí)厚度為多少?問題四:知道A4紙厚度與對(duì)折四處,那么對(duì)應(yīng)撕紙以后紙的厚度應(yīng)當(dāng)怎樣計(jì)算?問題五:對(duì)以上問題進(jìn)行觀察,想一想上述數(shù)據(jù)間存在什么聯(lián)系?是否存在函數(shù)關(guān)系?把可視化的實(shí)踐活動(dòng)與變式問題進(jìn)行結(jié)合,完成導(dǎo)入情境的創(chuàng)設(shè),可以引導(dǎo)學(xué)生進(jìn)行思考以及逐步探究,逐漸引導(dǎo)高中生對(duì)指數(shù)函數(shù)進(jìn)行認(rèn)識(shí)以及探索.
二、在概念教學(xué)當(dāng)中應(yīng)用變式
眾所周知,數(shù)學(xué)概念乃是數(shù)學(xué)知識(shí)當(dāng)中的重要部分,其是數(shù)學(xué)知識(shí)這一體系的重要脊梁.高中生只有對(duì)數(shù)學(xué)概念進(jìn)行有效理解以及掌握,才可以對(duì)數(shù)學(xué)知識(shí)進(jìn)行掌握.而在概念教學(xué)當(dāng)中應(yīng)用變式,可以引導(dǎo)高中生對(duì)數(shù)學(xué)概念進(jìn)行全面認(rèn)識(shí),促使高中生對(duì)于概念內(nèi)涵以及外延進(jìn)行深入理解,把數(shù)學(xué)概念進(jìn)行有效聯(lián)結(jié),進(jìn)而讓整個(gè)概念體系變得越發(fā)豐富以及完善,讓高中生對(duì)于數(shù)學(xué)知識(shí)進(jìn)行深入認(rèn)識(shí)以及理解.
比如,進(jìn)行“拋物線”教學(xué)期間,數(shù)學(xué)教師可引導(dǎo)高中生由典型問題著手,借助變式逐漸對(duì)知識(shí)體系進(jìn)行完善.典型問題為:A(a,3)為拋物線y2=2px上的點(diǎn),已知其和拋物線的焦點(diǎn)間距離是4,求a值與p值.
分析上述問題屬于典型基礎(chǔ)問題,針對(duì)學(xué)生而言,套用公式便可快速求出答案.教師教學(xué)可將基礎(chǔ)實(shí)施變式,進(jìn)而推動(dòng)學(xué)生對(duì)知識(shí)進(jìn)行全面理解.
變式1已知一個(gè)動(dòng)點(diǎn)A到直線x+4=0的距離和其到定點(diǎn)P(2,0)距離的差為2,求點(diǎn)A的軌跡方程.
通過變式1,高中生可以對(duì)拋物線之上點(diǎn)運(yùn)動(dòng)軌跡進(jìn)行深入研究,和典型問題相比,變式1這個(gè)問題可以促使高中生對(duì)基礎(chǔ)概念進(jìn)行理解.
變式2已知點(diǎn)P坐標(biāo)是(6,4),而且拋物線x2=4y之上存在一個(gè)動(dòng)點(diǎn)A,求A到點(diǎn)P間的距離和其到x軸距離之和的最小值.
變式2是在變式1基礎(chǔ)之上進(jìn)行的提高,難度加大很多.然而,緊扣拋物線這個(gè)核心概念,由基礎(chǔ)題到兩個(gè)變式問題,問題難度不斷提高,可以促使高中生的數(shù)學(xué)思維逐漸發(fā)展,促使其對(duì)基礎(chǔ)概念進(jìn)行透徹以及全面理解.
針對(duì)概念教學(xué)來說,通過變式可以幫助高中生對(duì)概念進(jìn)行深刻理解,進(jìn)而為其深入學(xué)習(xí)奠定扎實(shí)基礎(chǔ),有效培養(yǎng)高中生的數(shù)學(xué)思維.
三、在探究活動(dòng)當(dāng)中運(yùn)用變式
若想提升數(shù)學(xué)教學(xué)的整體效果,教師需引導(dǎo)高中生對(duì)數(shù)學(xué)知識(shí)進(jìn)行自主探究,突出高中生具有的主體地位.所以,數(shù)學(xué)教師可把探究活動(dòng)和變式進(jìn)行結(jié)合,通過變式問題來引領(lǐng)高中生對(duì)知識(shí)展開深入探究,這樣可以促使教學(xué)效果不斷提升.當(dāng)高中生完成學(xué)習(xí)以后,可以有效提高高中生的數(shù)學(xué)素養(yǎng)以及探究能力.
比如,進(jìn)行“等差數(shù)列”教學(xué)期間,數(shù)學(xué)教師可通過下面變式問題引導(dǎo)高中生展開思考以及探究.
現(xiàn)有一無窮的等差數(shù)列,而且已知該數(shù)列的首項(xiàng)是a1,公差是d,對(duì)下列問題進(jìn)行思考以及探究.
問題一假設(shè)把這個(gè)數(shù)列當(dāng)中前m項(xiàng)都去掉,用其他各項(xiàng)構(gòu)成一個(gè)新的數(shù)列,問新構(gòu)成的數(shù)列是否依然為等差數(shù)列?如果是等差數(shù)列,求出這個(gè)新數(shù)列的首項(xiàng)以及公差;如果并非等差數(shù)列,說明具體理由.
問題二假設(shè)把原數(shù)列當(dāng)中奇數(shù)項(xiàng)全部取出來,依次構(gòu)成一個(gè)新的數(shù)列,問新構(gòu)成的數(shù)列是否依然為等差數(shù)列?如果是等差數(shù)列,求出這個(gè)新數(shù)列的首項(xiàng)以及公差;如果并非等差數(shù)列,說明具體理由.
高中生在對(duì)等差數(shù)列進(jìn)行學(xué)習(xí)期間,常常會(huì)遇到困難,假設(shè)直接忽略概念教學(xué),直接對(duì)概念進(jìn)行運(yùn)用,常常會(huì)讓高中生的思維出現(xiàn)脫節(jié)現(xiàn)象,而且還會(huì)對(duì)教學(xué)效果造成較大影響.而通過變式把概念教學(xué)變成具體問題,高中生在對(duì)具體問題加以解決期間,可以主動(dòng)進(jìn)行思考,而且所有變式可以有效撞擊高中生思維,有效提升高中生的認(rèn)知能力.
四、在習(xí)題教學(xué)當(dāng)中應(yīng)用變式
在高中階段的數(shù)學(xué)教學(xué)之中,習(xí)題教學(xué)屬于重要課型,通過習(xí)題教學(xué)能夠讓高中生在解題當(dāng)中對(duì)所學(xué)知識(shí)進(jìn)行運(yùn)用,幫助其對(duì)所學(xué)知識(shí)進(jìn)行不斷內(nèi)化,進(jìn)而培養(yǎng)高中生的解題能力,發(fā)展其數(shù)學(xué)思維,有效培養(yǎng)其核心素養(yǎng).在習(xí)題教學(xué)當(dāng)中對(duì)變式加以運(yùn)用,可以幫助高中生實(shí)現(xiàn)舉一反三,通過解答幾道問題而掌握一類問題的解答方法,進(jìn)而提升其學(xué)習(xí)效率.
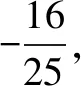
解設(shè)M點(diǎn)的坐標(biāo)為(x,y),由題意可得:
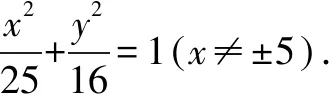
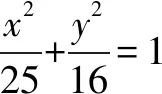
變式1假設(shè)點(diǎn)A與點(diǎn)B坐標(biāo)為(-5,0)及(5,0),AM與BM交于點(diǎn)M,而且其斜率的積為m,同時(shí)m≠0,試求點(diǎn)M軌跡方程.
解設(shè)M點(diǎn)的坐標(biāo)為(x,y),由題意可得:
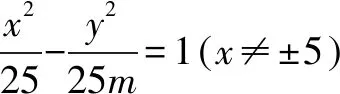
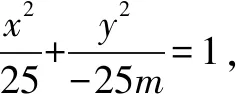
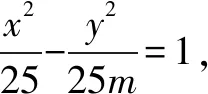

解設(shè)AM與BM斜率的積是k,由題意可得:
通過上述變式訓(xùn)練,可以幫助高中生對(duì)橢圓軌跡問題的解答方法進(jìn)行有效掌握.
綜上可知,在高中階段的數(shù)學(xué)教學(xué)之中進(jìn)行變式教學(xué),可以有效發(fā)散高中生思維,幫助高中生對(duì)所學(xué)知識(shí)進(jìn)行內(nèi)化,促使其綜合能力不斷提升.數(shù)學(xué)教師可在情境創(chuàng)設(shè)、概念教學(xué)以及習(xí)題教學(xué)當(dāng)中應(yīng)用變式,這樣可以促使教學(xué)效果不斷提升.

