旋轉液體液面形狀的幾種解法

程震驚

(新疆生產建設兵團第二中學，新疆 烏魯木齊 830002)

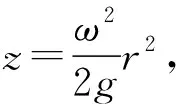
題干中介紹了旋轉液體的液面為旋轉拋物面，據此考察了液體旋轉前后，液面高度的變化和一些幾何光學的知識.但是很多學生對于旋轉液體液面形狀形成的緣由并不清楚，后續處理一些相關內容時，會感到棘手.筆者對該問題，使用不同的方法，從不同的角度進行說明.

圖1

在重力的作用下，假設旋轉液體的液面達到穩定狀態.如圖1所示，取坐標原點在液面的最低點，縱坐標軸z與圓柱器皿的軸線重合，橫坐標軸r與z軸垂直.

方法1.由于液面達到穩定狀態，取液面上(r，z)處，某一質量為m的小液滴作為研究對象.小液滴在重力mg和支持力N的共同作用下做勻速圓周運動，角速度為ω.則小液滴受到的合力為

F合=mgtanθ=mω2r，

其中r是小液滴到z軸的距離，而

進而得到液面微分方程

解得

代入初始條件，ω=0時，z=z0，其中z0為液體沒有旋轉時液面的z軸坐標，得

為拋物線，繞z軸旋轉可得旋轉拋物面.

圖2

方法2.取旋轉的圓筒為參考系，為非慣性參考系.由于液面達到穩定狀態，對于某個質量m的小液滴而言，即達到了受力平衡狀態.因此，有小液滴受到重力mg，支持力N，慣性離心力F慣=mω2r，3個力的合力為0，如圖2所示.小液滴沿液面切線方向受力平衡，有

mgsinθ=mω2rcosθ，

而

進而得到液面微分方程

后續解法同方法1.

圖3

方法3.取液面上某一點(r，z)到z軸的距離對應的水平細液柱為研究對象，如圖3所示.

化簡得

圖4

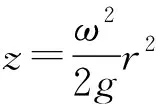
為拋物線，繞z軸旋轉可得旋轉拋物面.

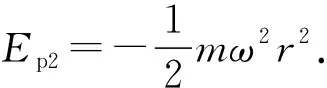
得

為拋物線，繞z軸旋轉可得旋轉拋物面.

容器轉動帶動液體旋轉，旋轉液體液面的形狀為旋轉拋物面.這是物理學中的一個重要物理現象.光學儀器、雷達天線等越來越多的領域利用這個物理現象進行科學研究和實驗.掌握其不同的推導證明方式，有助于提高學生的學習興趣，有利于學生物理學科核心素養的培養.