深度教學，讓學習真正發生

許新新

[摘 要]深度教學是近些年教學研究倡導的一個熱點。實施深度教學，數學教師要采取以下策略：從深度挖掘數學知識的文化背景著手，促進學生思維提升;從深度剖析數學問題產生、解決過程發力，促進學生思維生長;從深度解析數學認知建構方面主攻，設計充分有效的數學活動，讓學生深刻感悟其中的思維策略;從解析數學知識運用方面引導，展現方法多樣化，引導學生思維的靈活和創新。

[關鍵詞]深度教學;深度解析;思維

[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068（2021）35-0052-02

深度教學是近些年教學研究的一個熱點。小學數學教師實施深度教學，必須著力深度解析知識來由、學習活動、策略運用和方法探究，以推動和引導學生深度學習。數學教師可以采取以下策略，引導學生深度掌握知識，并學會靈活運用和實現思維創新。

一、深度挖掘知識文化背景，促進學生思維提升

在教學數學新知識時，激發學生學習興趣，使之具有探索和主動學習的欲望，是促進學生深度學習和提升思維的前提條件。教師可以深入挖掘數學知識的文化背景，以及相關的數學故事、數學史等數學文化，并相機穿插滲透，讓學生興趣滿滿，熱情高漲。

比如，圓是教師和學生再熟悉不過的平面圖形，然而他們未必都真正了解圓的相關背景知識。數學教學中如何滲透圓的文化，讓學生認識圓的本質，促進學生思維的提升，是需要教師深入思考的問題。

最具人類文明標志性元素之一的“輪子”，抽象地看就是“圓”。生活實踐中，人們發現輪子越大，轉過一周的距離越長。于是人們開始深究：轉動的距離與輪子的直徑長短有什么關系？進而研究圓與直徑的關系，以揭示“輪子也就是圓”的奧秘。

教學中，引導學生簡要回顧人類研究圓的歷程：從初步認識圓形物體到借助圓形物體得到一個圓;從用圓規畫圓到計算圓的周長、面積等;從單獨研究圓到研究圓與其他圖形的組合;從以滾動實驗初步體會圓周率的計算方法到圓的封閉、對稱之美。在學習圓的過程中，圓周率是學生很感興趣，也是印象最深刻的。對此，教師可以穿插滲透相關數學文化，如公元263年我國魏晉時期數學家劉徽由割圓術得到3.1416，稱為“徽率”;1200年后，西方人才找到類似于劉徽的計算方法。到公元480年，我國南北朝時期數學家、天文學家祖沖之概括“割圓術”，得出圓周率在3.1415926與3.1415927之間，還用22/7和113/355這兩個分數（稱為“約率”和“密率”）作為圓周率的近似數值。這個記錄保持了近千年。計算機的出現使圓周率的計算有了突飛猛進的發展，到二十一世紀六七十年代得到圓周率一百萬個小數位數值。

深度解析圓的背景知識及其研究歷程，以及不同時期圓周率的發現發展過程，能激發學生對數學文化的學習興趣，讓學生學會更全面、更完整地思考數學知識，從而促進學生深度學習。

二、深度剖析問題產生與解決過程，促進學生思維生長

美國當代數學家哈爾莫斯曾經說過：“問題是數學的心臟。”發現問題、提出問題、分析問題、解決問題貫穿在整個數學教學中。數學教師要引導學生深入探究問題的產生過程與解決方法，對問題前瞻、后顧，用問題引領學生深入學習，從而進一步促進學生思維生長。

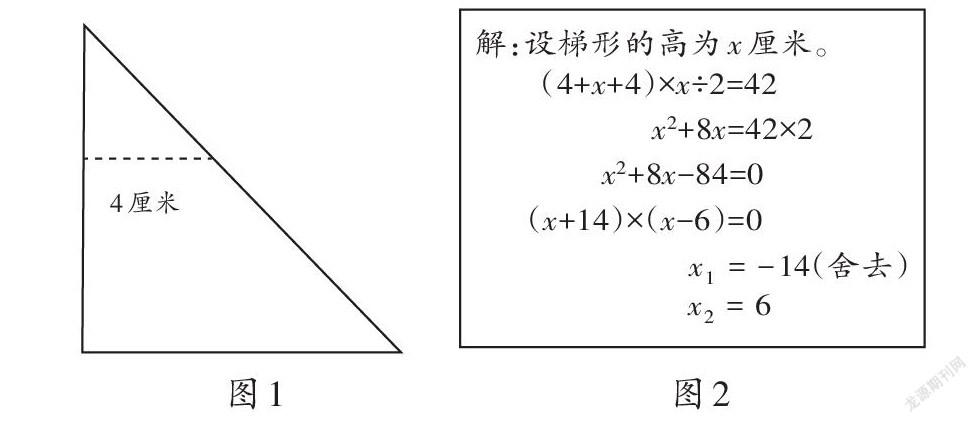
比如，著名特級教師王九紅在一次教學中給學生出示思考題：將一個等腰直角三角形剪掉一個三角形后得到一個梯形（如圖1）。已知梯形的面積是42平方厘米，上底長4厘米，梯形的高是（? ）厘米。

上例中剪掉的三角形是一個等腰直角三角形，根據梯形的面積公式可以列出如圖2所示的方程，方程為一元二次方程，超出了五年級學生的接受范圍，難度大。基于此，教師從問題出發進行針對性引導。

師：如果設梯形的底為x呢？

生1：（x+4）（x-4）÷2=42。

師：這個方程和之前的方程有什么區別？

生2：這個方程簡潔、對稱，容易解答。

師：你能把“÷2”移到右邊再解答嗎？

生3：可以。方程兩邊同時乘2，得到（x+4）（x-4）=42×2。

師：方程右邊的“42×2”表示什么？

生4：42×2表示梯形面積42的兩倍。

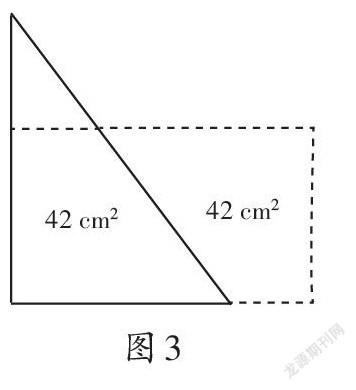
師：如圖3，梯形的高也就是長方形的寬。那么，可用什么方法解（? ）×（? ）=84？

生5：可用一一列舉法分解84的因數。

師：很好！請說具體些。

生5：84=1×84=2×42=3×28=4×21=6×14=7×12。經過驗證得知長方形的寬是6厘米。

……

以上解答過程中，教師拋出問題“如果設梯形的底為x呢？”引發學生思考，學生列出另外一種方程，體會到解方程可以由直接設未知數變為間接設未知數，從而促進學生思維不斷生長。

三、深度解析數學活動過程，感悟探究方法

數學活動不僅僅是動手實踐，還包括各種數學運算、思維推理、解決實際問題等。在教學活動中，往往出現學生只知道呆板地算，不總結，不歸納，不思考，這是數學活動無法有效開展的表現。引導學生發現相應數學規律，完成算法歸納， 實現方法優化，是數學計算活動的重要任務。

例如，蘇教版教材三年級上冊第一單元“有趣的乘法計算”一課，在探索“同頭尾合十”的兩位數乘兩位數計算規律時，教材首先呈現了三道豎式“22×28”“35×35”“56×54”，要求學生仔細觀察、比較算式，并說說它們有什么共同特點，讓學生在討論和交流中逐步明確這些算式都是兩位數乘兩位數，且每個算式中的兩個乘數：十位上的數是相同的——“同頭”;個位上的數相加正好等于10——“尾合十”。在此基礎上，要求學生算出每個算式的乘積，繼續觀察、比較得到的各個乘積，適當啟發學生思考：所得的積的末兩位各是多少？各是由哪兩個數相乘得到的？積的末兩位前面的數各是多少？它們又可看作哪兩個數的乘積？由此，完成抽象概括：積的末兩位是兩個乘數個位上的數相乘的積，而末兩位前面的數則是兩個乘數十位上的數與比它大1的數相乘的積。這里的教學活動重點關注數據現象中隱含的特征，把握變化中不變的共性。讓學生如此經歷數學活動，有助于他們順利總結，形成計算經驗。

四、深度解析多樣化思考路徑，深層培養思維品質

鄭毓信教授曾說：“數學深度教學的一個重要內涵，應當由突出強調具體的數學方法和策略，轉變為注重一般性思維策略和思維品質的提升。”數學方法和策略是思維策略和品質提升的一個重要手段，教師應抓住本質，追求數學方法的靈活多樣，以培養學生思維的靈活性，從而達到深度教學的目的。

例如，喝幾瓶汽水問題：每3個空汽水瓶能換到一瓶汽水。現在買了10瓶汽水，一共能喝到多少瓶汽水？

方法一：操作演示。拿出10瓶汽水，實際操作演示，最終發現剩余2瓶汽水，需要借來1個空瓶（需還）湊足3瓶，喝完以后3個空瓶正好可換1瓶汽水，因此一共喝到15瓶汽水。

方法二：畫圖示意。

一共10瓶汽水，因為每3個空瓶換1瓶汽水，所以一開始能先換3瓶汽水，對應的這3個空瓶又換1瓶汽水，這1個空瓶加原來第10個空瓶再借1個空瓶可以換回1瓶汽水，還了借的空瓶后統計一共可以喝到15瓶汽水。

方法三：合情推理。3空=1瓶=1水+1空，3個空瓶可以換1瓶汽水，1瓶汽水就能喝到“1水”，剩“1空”，因此，2空=1水，也就是2個空瓶可以換1瓶汽水，一共有10瓶=10水+10空，10個空瓶可以換“5水”，所以10瓶=10水+5水=15水。買了10瓶汽水，可以喝到15瓶汽水。

方法四：推導計算。10× [1+12] =15，1瓶汽水喝掉算是“1水”，留下1個空瓶相當于“半（瓶）水”，一共10瓶汽水，也就是10瓶的[1+12]。

以上四種解題方法，每一種方法之間都有一根主線貫穿，即本題的本質：2個空瓶可以換1瓶汽水。如果思維深入這一層面，即可把問題順利解決。引導學生多途徑深度思考，深度解析題目本質，就能讓學生找到多種解題方法，從而培養學生思維的靈活性，有效提升學生的思維品質。

綜上，數學教學應超越具體知識和技能，深入到思維的層面，由具體的數學方法和解題策略過渡到一般性的思維策略與思維品質提升，從而有效培養學生的思維能力，促進學生深度學習。

[ 參 考 文 獻 ]

[1] 中華人民共和國教育部.義務教育數學課程標準（2011年版）[M].北京：北京師范大學出版社，2012.

[2] 鄭毓信.小學數學教師[M].上海：上海教育出版社，2019.

（責編 黃春香）