基于思維可視化的教學策略

劉品蘭 譚敏

[摘 要]很多學生在小學和初中階段學習優秀，但是到了高中階段就會在學習上感到困難，尤其是物理學科，這大都是因為思維方法上存在問題。理科思維應從小學階段開始培養，小學數學和高中物理在思維方法上是共通的，在小學數學教學中，教師培養學生的理科思維，可讓學生對后學段學習進行靈活遷移和應用。

[關鍵詞]小學數學;高中物理;思維可視化;理科思維

[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068（2021）35-0046-02

一、理論基礎

1.沉錨效應

沉錨效應，指的是人們在作決策和判斷時易受第一印象或第一信息支配，就像沉入海底的錨一樣把人們的思想固定在某處。按照這個理論，學生最早養成的思維習慣將會成為以后解決問題時最先依賴的思考方式。因此，在小學階段，教師就要讓學生勤于思考、重視過程與方法、形成良好的思維習慣，掌握對后學段學習有利的思維方式，為后學段的學習奠定良好的基礎。

2.遷移理論

在學習過程中，學生是信息加工的主體，是意義的主動建構者，而不是知識的被動接受者。在學習中，除了具體的知識，學生也會把以前掌握的思維方法，自覺地遷移應用到新知的學習中，從而構建自己的認知體系，并且這個遷移是沒有學科界限的。思維方法處于知識的上位，其掌握的程度決定著學生大腦中概念的抽象性、概括性和包容性水平。這些水平越高，學生舉一反三的能力就越強，思維越深刻，智慧水平越高。對此，小學階段就要讓學生在學習過程中掌握知識蘊含的思維方法，這能夠讓其在后學段的理科學習中提高學習效率。

二、小學數學思維與高中物理思維的聯系

學科的思維方法不是具體的學科知識，而是基于具體的學科概念、原理和定律。通過探討學科的內在特點和規律，整理和總結出來的思想觀念、思維方式和學習方法，能體現該學科的本質與價值，為學生提供了一種獨立學習、探究的方法，有助于提高學生問題解決能力和學科創新能力。

由于思維方法具有跨學科性，小學階段學到的數學思維方法也常被應用于物理學科的學習中。例如，小學畫圖解題的數形結合思維經常用來處理高中物理的運動圖像問題;小學數學解應用題中學到的程序思維用于處理多過程的物理問題;小學階段推導圓面積所用的逼近思想用于高中推導勻變速直線運動的位移和時間關系公式;小學數學中的等效替換的解題技巧常用于物理電路學問題中的等效電阻、等效電源等。

三、學生物理思維的現狀及應對策略

1.現狀

小學生的思維方式以感性思維為主，尤其在低年級，很多時候學生僅僅靠對知識的表層理解和記憶，就能在考試中取得不錯的成績。如果長時間使用這種功利化的教學方式，學生就容易養成懶于思考的不良習慣，錯過掌握相應思維方法的最好時機。當面對高中物理問題時，不會將對應的思維方法合理遷移到學習中，也無法將物理思維同化到已有的認識模式中。

2.應對策略

思維可視化就是指以圖示的方式把原本不可見的思維結構、思考路徑及方法變得可見的過程。它可以給以感性認識為主的小學生更加直觀和形象的理解。思考賦予了知識生命力，離開思考的學習必然是枯燥而低效的，提高教學效能的關鍵在于挖掘與呈現知識背后的思維規律并讓學生掌握它。因此，在平時的教學中，教師要讓學生主動思考和探究，利用思維可視化的策略，讓學生活動過程中的思維從不可見變得可見，提高學習效率。

四、教學案例

1.守恒的思維

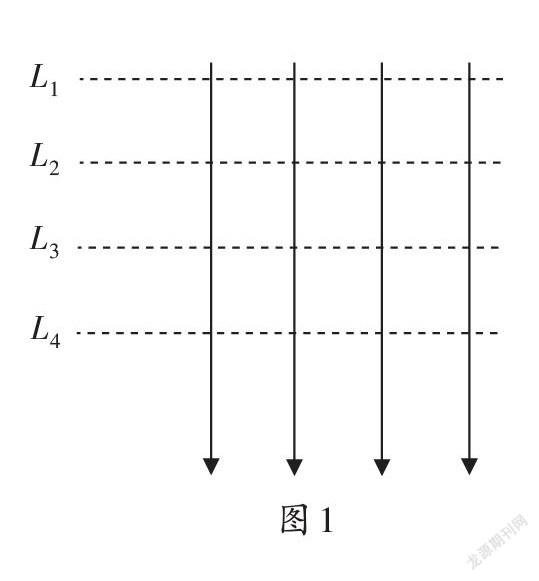
【例1】如圖1所示的勻強電場中，虛線為等差等勢面。一個正電荷在等勢面L3處的動能為20 J，運動到等勢面L1處時動能為零?，F取L2為零電勢參考平面，則當此電荷的電勢能為4 J時，它的動能是多少？（不計重力及空氣阻力）

這是高二物理靜電場中的一個常見問題，對初學者來說較難。該題目情景中僅有電場力做功，所以電荷的電勢能和動能此消彼長，總能量是守恒的，解決問題的關鍵就在于找出這個總能量。在小學數學學習中，也有很多類似的題目，教師可以在平時的教學中有意強化這種思維。

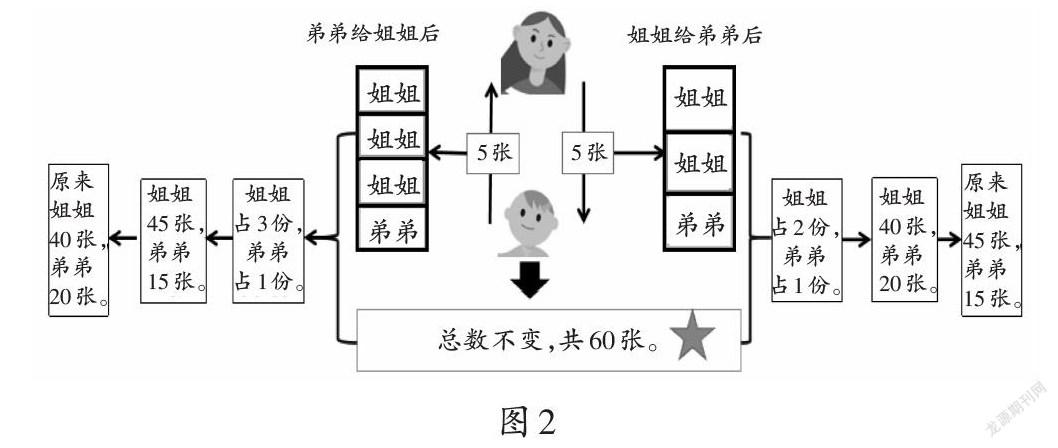
【例2】姐姐和弟弟共有60張郵票。（1）如果姐姐給弟弟5張后，姐姐的郵票數量是弟弟的2倍，姐姐和弟弟原來各有多少張郵票？（2）如果弟弟給姐姐5張后，姐姐的郵票數量是弟弟的3倍，姐姐和弟弟原來各有多少張郵票？

通過圖示（如圖2），首先明確無論姐弟之間怎么互給郵票，總數都是不變的。然后，引導學生找到最終姐弟各自的郵票在總份數中所占的份數，從而求出現在各自的數量，再推導出原來的數量。最后，再對這類題型進行總結，讓學生明白在解決問題中抓住守恒思維的重要性，理解在變化之中有不變，不變的量往往就是解決問題的突破口。

2.轉換的思維

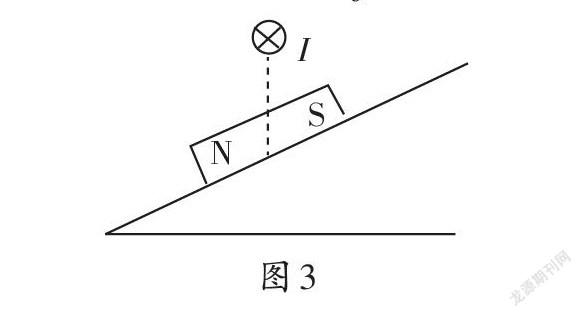
【例3】如圖3所示，一條形磁鐵靜止在斜面上，固定在磁鐵中心的豎直上方的水平導線中通有垂直紙面向里的恒定電流，如果增大導線中的電流，試分析磁鐵對斜面的壓力F和摩擦力f的變化情況。

這是高中物理中常見的題型，如果選用常規的思維直接研究磁鐵將很難入手，解題的關鍵是利用牛頓第三定律轉而思考導線的受力情況，通過轉換研究對象來解決問題。為了讓學生掌握這種思維方法，筆者在教學中選取了下面的題目。

【例4】小明的鉛筆支數是小華的3倍，如果小明給小華5支，小明比小華還多2支。兩人原來各有鉛筆多少支？

如圖4所示的思維過程中，無論這兩人之間怎么互給鉛筆，鉛筆總數不變。在給鉛筆之前，兩人的鉛筆數量之間有倍數關系，如果在給了鉛筆后仍然有倍數關系，那么這個問題就會變得容易一些，但是給了5支鉛筆后，他們之間的倍數關系不明確了。因此，可以將問題轉化為怎么給鉛筆能夠找到新的倍數關系。通過引導，學生發現當小明給小華6支鉛筆后，他們就一樣多了，再利用關系圖對比，就知道兩人各自原來的鉛筆數量。通過圖示對思維的具體表現，學生學會了將問題進行轉化來解決。

思維方法比具體的學科知識更重要，當學生學會把各個學科的思維方法加以綜合運用并跨學科遷移，其學習的效率和應用新知的能力也會得到提升。小學數學中蘊含著許多對高中物理乃至終身學習非常重要的思維方法，這就需要我們在小學階段有意識地強化學生對這些思維方法的掌握，全面提升學生的思維能力，為后面的學習做好準備。

[ 參 考 文 獻 ]

[1] 李維娜.“沉錨效應”下的教學及其反思[J].中小學數學：小學版，2019（10）.

[2] 張承芬.教育心理學[M].濟南：山東教育出版社，2010.

[3] 馬立麗，金洪源.提高學科學習能力的元認知策略與培養[M].沈陽：遼寧科學技術出版社，2016.

[4] 陳涵.淺談跨學科思想方法在高中物理教學中的融入[J].湖南中學物理，2020，35（08）.

[5] 陳涵.利用“思維可視化”培養高一學生物理解題思維[J].湖南中學物理，2017，32（06）.

（責編 李琪琦）