練得精巧 習得輕松

繆菊芳

[摘 要]課堂練習是教學活動的組成部分，對學生掌握新知識、形成基本技能以及靈活運用知識解決實際問題起著“橋梁”作用。在教學中，教師對課堂練習進行恰當處理、改造和設計，可加深學生對新知的理解和掌握，達到提高教學質量的目的。

[關鍵詞]課堂練習;設計;思維

[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068（2021）35-0041-03

數學課堂練習是教學活動過程中的重要一環，它既是學生掌握、鞏固知識，形成基本技能、發展思維的重要途徑，也是提高學生運用知識解決實際問題能力的有效平臺。課堂練習的時間基本占到了半節課，可見其重要性。作為教師，如何合理有效地設計課堂練習？在不加重學生課業負擔的情況下，摒棄反復操練，對課堂練習進行恰當處理、改造和設計，提升學生的數學應用意識，激發學習興趣，培養創新意識，是一個值得探討的問題。下面，結合教學實例，談談筆者對數學課堂練習設計的一些思考。

一、注重習題間的對比，培養審題能力

對比練習是課堂中一種常用的教學方法，它將一些容易混淆的題目組成題組進行比較，以引導學生抓住聯系、辨別差異，破除思維定式。在比較、分析中，學生既能加深認知、內化知識，又能培養審題能力，促進創新思維向深度發展。

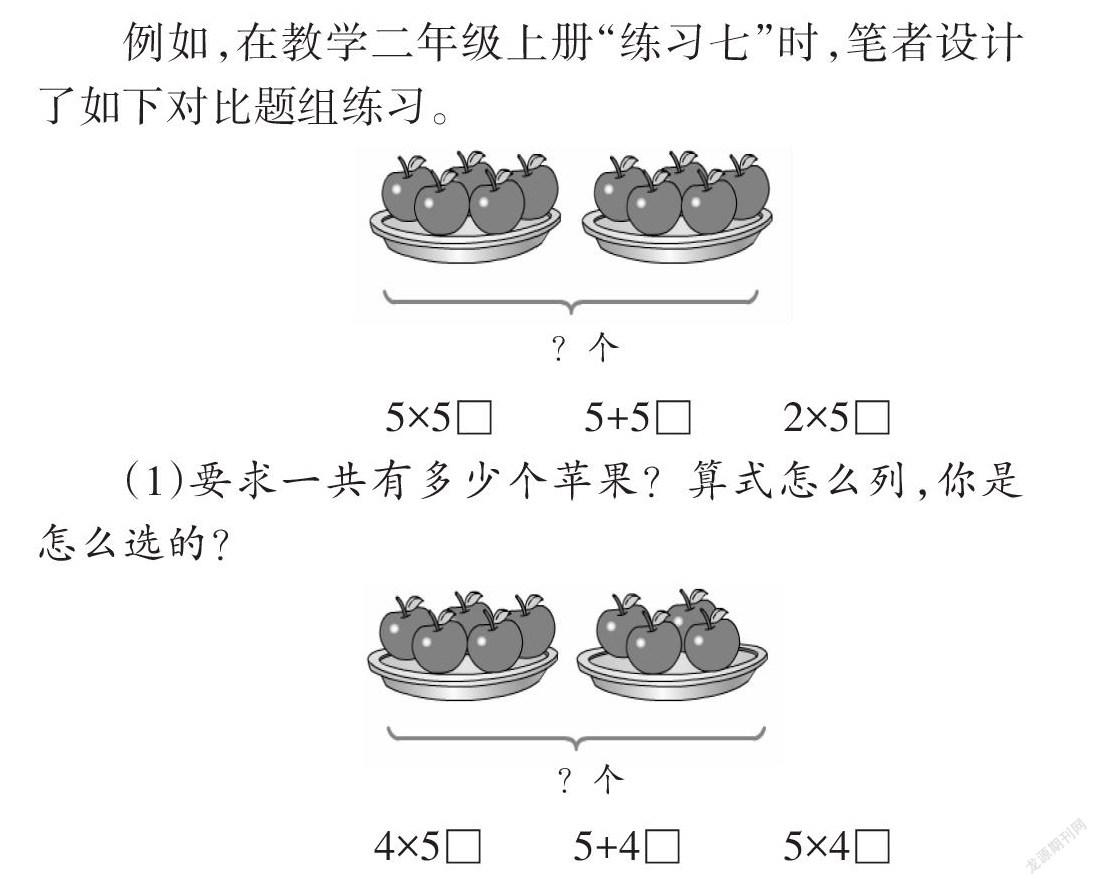
例如，在教學二年級上冊“練習七”時，筆者設計了如下對比題組練習。

（1）要求一共有多少個蘋果？算式怎么列，你是怎么選的？

（2）這幅圖又表示什么意思？該怎樣列式呢？誰來說說你是怎么選的？

（3）同樣是求兩盤蘋果的總數，為什么題（1）既可以用加法又可以用乘法，而題（2）只能用加法？

上述教學案例是學生在學完乘法口訣后的練習課，通過對兩幅圖中蘋果總數的比較，讓學生明白：兩個加數相同時可以改寫成乘法，而兩個加數不同時只能用加法。這樣的對比，既幫助學生厘清了加法和乘法的意義，也幫助學生區分了加法和乘法之間的異同點。此后，學生再碰到類似問題就具有了一定的審題能力，能夠靈活應用，找到解題方法。

二、注重練習的實踐性，發展感知能力

動手操作是學生學習數學的重要方式和方法。教育家皮亞杰說過：“知識來源于動作，而非來源于物體。”組織學生進行操作活動，在活動中觀察、實驗、猜測、驗證、推理和交流，學生定會學得更主動。對此，在練習中設計一些體驗性強的操作活動，不僅能調動學生的學習熱情，也能使學生在探索中獲得經驗、知識，這也是發展學生感知和思維的重要方式。

例如，在教學二年級下冊“時、分、秒”時，為了讓學生感受1分鐘有多長，筆者設計了如下練習。

（1）集體體驗1分鐘。

師： 1分鐘有多長呢？我們一起來靜靜地體會這1分鐘。

師：你覺得這1分鐘長嗎？

師：在靜靜等1分鐘時，有人覺得長，有人覺得短。

（2）估計一下，1分鐘你能做哪些事情呢？

師：1分鐘你能寫多少個字？做多少道口算題？

（3）分組體驗1分鐘。

師：這1分鐘你感覺怎么樣？

師：同樣1分鐘，由于所做的事情不同，感受也會不一樣。

師：你在1分鐘里寫了幾個字？在1分鐘里能做幾道口算題呢？

師：你看，1分鐘它說長不長，說短不短，我們好好利用，還是能做很多事情的。因此，我們要珍惜每一分鐘，做好每一件事。

讓學生感知1分鐘的時長，并建立1分鐘的時間觀念是有一定難度的。教學時，通過組織學生體驗感知1分鐘的時長活動，在體驗活動中產生認知沖突，并逐步建立1分鐘時長的清晰表象，突破了教學難點。這樣的設計使學生的學習變被動為主動，真正成為學習的主體，從中獲得真實的感知。

三、習題“小題大做”，培養思維靈活性

練習設計有時可以不止于題目中的問題，還可對原題中的條件和問題加以拓展，充實練習內涵，有助于學生掌握新知識，強化學習能力，豐富數學思考，培養思維的靈活性。

例如，在教學“倍的認識”時，在學生建立“倍”的概念以及初步掌握“求一個數是另一個數的幾倍”的基本思考方法后，筆者設計了如下練習。

（1）先估一估，第一條線段的長度是第二條的幾倍？再量一量、算一算。

（2）如果第二條線段增加1厘米，就變成4厘米，現在第一條線段的長度是第二條的幾倍？

（3）在第二問的基礎上，如果第一條線段也增加1個4厘米，就變成16厘米，現在第一條線段的長度是第二條的幾倍？

原題只是讓學生估一估、算一算，得出第一條線段的長度是第二條的4倍。通過對原題中的條件進行拓展，如題（2）讀到“第二條線段增加1厘米，就變成4厘米”后，可知原來第二條線段長3厘米，第一條線段長12厘米，最終得出現在第一條線段的長度是第二條的3倍。設計這個問題的目的是通過一倍數的變化，進一步鞏固學生對“倍”的概念以及“求一個數是另一個數的幾倍”的基本思考方法的理解。緊接著題（3）中“第一條線段也增加1個4厘米，就變成16厘米”得出現在第一條線段的長度是第二條的4倍。這個問題的解法并不是唯一的，方法一：先算出第一條線段有多長，12+4=16（厘米） ，再進行除法計算， 16÷4=4。方法二：第二問后，第一條線段的長度是第二條的3倍，這時把第一條線段增加1個4厘米，就是又多了1倍，3+1=4，所以現在第一條線段的長度是第二條的4倍。這個問題再次加深了學生對“倍”的認識，同時方法二結合線段圖解釋時，學生直觀認識到多了1個4厘米就是又多了1倍，拓寬了學生解題的思路，體會學習方法的多樣性，培養了思維的敏捷性和靈活性。

四、注重練習的綜合性，提升思維品質

練習的形式是多樣的，除了基本練習、變式練習，教師還應該考慮綜合性練習。在設計練習的同時幫助學生把新知及時納入原有的知識系統中，使新舊知識相互融合，以培養學生綜合運用知識的能力。

例如，在教學“求比一個數多（少）幾的實際問題”時，筆者在課后設計了如下練習。

（1）停車場有面包車30輛，? ? ? ? ? ? ? ? ?，小汽車有多少輛？

①小汽車比面包車多8輛

②小汽車比面包車少8輛

③小汽車和面包車一共有50輛

④大卡車比面包車少18輛

選（? ?）是用加法計算，選（? ?）是用減法計算。

（2）停車場有面包車30輛，? ? ? ? ? ? ? ? ?，小汽車有多少輛？

①30-8=22（輛）

②30+8=38（輛）

如果在橫線上填“比小汽車少8輛”，選（? ?）號算式計算。

如果在橫線上填“比小汽車多8輛”，選（? ?）號算式計算。

題（1）根據不同的計算方法選擇缺少的條件，題（2）根據補充的條件選擇相應的計算方法。在課后增設“一題多變”的綜合練習，打破了學生的順向思維，對學生來說還是很有挑戰性的。把之前學過的一些簡單實際問題和現在學習的這類問題串聯起來，將前后知識有機整合，讓學生認識到在解決實際問題時要認真審題，仔細分析前后聯系，不能看到“多”就用加法，看到“少”就用減法，從而發展學生的思維靈活性、廣闊度、發散性，優化思維品質，提高學生解決實際問題的能力。

五、注重練習的開放性，促進積極思考

有效的數學學習過程不能單純地依賴模仿和記憶。基于“不同的人在數學上得到不同的發展”的理念，教師在設計練習時必須具備開放性，滿足學生的不同需求。對此，在設計練習時，除了要有基本的練習題，還要增加一些開放性的習題，讓學生“跳一跳，摘果子”。這樣，學有余力的學生也能在解題過程中表現出強烈的挑戰欲望，產生濃厚的學習興趣。

例如，在教學一年級上冊“10的分與合”時，在全課總結后，筆者設計了一道開放性練習題。

[6][8][10]

（1）這道分合式比較復雜，你能看得懂嗎？

（2）在這4個框中，你覺得要先填哪幾個框？

（3）你能有次序地寫出所有填法嗎？

在課的結尾增設一道這樣的開放性練習題，把學生原來認識的單一分合形式變成多種分合形式，對學生來說是認知的一個突破。首先，學生通過觀察發現這道題其實可以看成“6可以分成幾和幾”“8可以分成幾和幾”“幾和幾合成10”三部分的組合，再引導學生深入思考，發現在這4個框中，中間2個框是關鍵，要先填，最后讓學生有次序地寫出所有填法。這樣的開放性練習，既培養了學生觀察問題、分析問題和解決問題的能力，也培養了學生思考問題的全面性。

六、注重練習的趣味性，增強學習主動性

計算是數學學習的基礎，但計算教學的練習對學生來說比較枯燥，總是出題、解題的模式學生也會感到厭倦，失去學習的熱情。把練習題進行包裝，設計成學生喜歡的形式，如小游戲、闖關活動，就能大大激發學生的學習興趣，增強學習的主動性，使枯燥的計算課變得靈動有趣。

例如，在教學“兩位數加減兩位數筆算”時，筆者在練習環節設計了闖關比賽：第一關——計算小能手;第二關——爭當小法官;第三關——筆算小達人。第一關是基礎題，以鞏固學生的筆算方法為主;第二關是改錯題，主要解決學生經常出錯的運算符號和對位問題;第三關是筆算小練習，經過前兩關的訓練，學生的錯誤率大大降低。闖關比賽的設計是根據兒童的心理特點和學習需求，通過對課本上的三組筆算題進行改編，學生在掌握筆算方法、提高計算正確率的同時，學習的興趣也變得濃厚，切實提高了教學效果。

課堂練習不是單一地做題，而是把培養學生的學習情感、學習興趣、動手能力、創新意識等融入其中，設計多種形式的練習題，讓練習內容豐富起來，真正為學生的發展服務，讓學生練得精巧、習得輕松。教師在平時教學中要不斷地反思、積累經驗、歸納總結、用心設計，以獲得實施練習設計的最佳效果，從而提升教學質量。

[ 參 考 文 獻 ]

[1] 楊惠娟.教材習題使用誤區及資源開發策略[J].教育研究與評論：小學教育教學，2012（10）.

[2] 唐其梅.小學數學練習設計要有“趣”[J].新教育，2019（20）.

（責編 李琪琦）