“先學后教”理念下的校本作業開發與實踐*
福建省廈門實驗中學 (361116) 黃耿躍福建省廈門第一中學 (361000) 李蓉蓉
國家中長期教育改革和發展規劃綱要要求:“減輕中小學生課業負擔,學校要把減負落實到教育教學各個環節,給學生留下了解社會、深人思考、動手實踐、健身娛樂的時間.”但受應試教育影響,有些教育工作者急功近利,導致以知識落實為主的作業成為教師搶占學生課后時間的重要武器,以布置大量作業,換取學生成績提高為手段,造成學生對作業的厭煩,甚至厭惡,使一部份的學生成績反而更差、跟不上.
筆者所在學校,廈門實驗中學是一所新辦校,學校在開辦時就設計好校本作業開發與實施方案,要求學生統一不訂閱教輔材料,每天的作業都由老師自己選題、組題.辦學7年來,高考取得令人矚目的成績,這與學校制定的“五個四”校本作業體系的辦學指導思想是密不可分的.本文是筆者站在數學科的角度,就如何開發、實施”五個四校本作業“談談自己的一些做法.
一、“五個四”校本作業概念界定
“五個四”校本作業:指四案、四精、四必、四合、四查.
1.四案:指學案、 作業、 課練、 周練.學案是新授課課前發給學生,由學生自主閱讀課本并完成學案內容,內容主要包括“知識梳理、重難點問題記載、自主檢測、總結反思” 四個模塊,達到預習新知的目的.作業與學案相配套,是課后對學生所學知識的鞏固練習.學案與課后作業穿插進行,實行小單元教學法.
2.四精:指精選、精練、精講、精評.四案中的問題老師要先做一遍認真精選,題量控制,讓學生跳出題海,達到精練的目的;通過學案引導學生先學先做,在學生先學的基礎上老師再精講,學生會的不再講;課后作業也是學生先做的基礎上,教師從知識重難點和學生易錯點兩方面剖析題目.四精是四案質量的保障.
3.四必:指必發、必收、必改、必評.對四案中的校本作業,學案要提前1至2天發到學生手中,讓學生先學先做,老師收改后再進行施教;課后作業、周練也是讓學生先做,老師收改后及時講評;課練應當天批改當天發還學生手中,讓學生及時訂正,及時強化知識點,第二天講評.四必是實施四案校本作業的重要過程.
4.四合:指與作業的八個要求(統一布置、分層要求、先做后講、全批全改、個別輔導、點評到位、人人過關)相結合、與五步學習法(預習、上課、作業、復習、總結五個環節)相結合、與考點教學法相結合、與家教式輔導相結合.四個結合是四案校本作業細化層面的具體內涵.
5.四查:指查四案質量、查校本作業落實情況、查存在問題、查效益.四查是對四案校本作業補漏提質的重要環節.
二、校本作業開發與實施
零點問題是高考中的重要考點,也是高考的難點,所以學生只有通過先行做題,再聽老師講解,最后再進行類題訓練,才能達到鞏固、強化,真正理解消化、掌握技能的目的.按照我校校本作業的開發與實施理念,高三年總復習時,對零點存在定理這一重要知識的復習安排,我們會先在學案中安排如下兩道解答題,目的是讓學生初步學會如何利用零點存在定理解決問題,特別是突破如何取點的問題.
題1 已知函數f(x)=ex-ax(a∈R)存在兩個零點,求實數a的取值范圍.
題2 已知函數f(x)=lnx-ax(a∈R)存在兩個零點,求實數a的取值范圍.
設計意圖:兩個常見的超越函數ex,lnx與一次函數的簡單組合,是學生熟悉的函數,與高考試題的命題思想是相吻合的,讓學生拿到作業感到親切,有想做、敢做的沖動.同時,兩道題目蘊涵豐富的思想方法,可全面訓練學生利用導數研究函數的單調性,零點存在定理中端點值的取法,不等式的切線放縮法及分類討論思想、數形結合思想等.
下面就如何利用題1揭示問題本質,進行精講、精評、精析.
第一步,對函數進行求導,利用導數研究函數的單調性.∵f′(x)=ex-a,∴f′(x)>0?x>lna,f′(x)<0?x (師:結合函數的圖象特征可知f(lna)為函數的極小值,要使函數存在兩個零點,則必需滿足f(lna)<0,從而可求得a>e,但要注意a>e是結論成立的必要條件.所以,必需在lna的兩側各找到一個點的函數值大于0,才能說明a>e是所求的范圍.) 第二步,利用零點存在性定理,找端點的函數值正負.∵f(-1)=e-1+a>0, (師:顯然,只要x<0的任意一個數,都能使f(x)>0成立,所以這個點是比較好取的,結合函數的單調性,也就意味著在區間(-∞,lna)上必存在唯一的零點.) 綜上所述a>e. 題2的講解與題1的講解類似,限于篇幅,請讀者自行完成. 在課練和周練中,我們再選2道高考題變式,目的是讓學生通過聽完老師的講解,通過自己的領悟,利用所學到的思想方法,進一步解決如下兩道問題.因為課練和周練都是限時訓練,有時間限制,所以通過課練或周練的形式,可以真正檢測學生的學習效果. 題3 (2017年全國Ⅰ卷理科變式)已知函數f(x)=ae2x+(a-2)ex-x,若f(x)存在兩個零點,求實數a的取值范圍. 題4 已知函數f(x)=(x-2)ex+a(x-1)2(a>0),若f(x)存在兩個零點,求實數a的取值范圍. 下面就如何利用題3揭示問題本質,進行精講、精評、精析. (師:這種取點判斷函數值的正負問題,一般情況下,左右兩邊有一個數是比較好取的,可以通過觀察得到,而另一邊的點一般是帶有參數的點.) 綜上所述,當0 題4的講解與題3的講解是類似,限于篇幅,請讀者自行完成. 我校“五個四”校本作業實施3年來,數學組的成績取得較大的進步,從廈門市歷次的質檢和3次省質檢成績可以佐證.如果不是實施校本作業,對函數零點存在定理的復習,我們也無法根據學生的實際情況,編寫四道有針對性的問題展開復習,這是真正體現“因材施教”的教學原則,真正體現“因地制宜”的教育思想.先學后教的理念在“五個四”校本作業得到完美詮釋,有利于真正培養學生自學能力.因為學生長期以來都是帶著問題在學習、在聽課、在反思,這對提高學生分析問題、解決問題的能力是潤物細無聲的.由于“四案”的作業量始終保持在12道題,這種題量對學生來講是最適合的.優秀生在完成作業后,可以騰出時間自主安排,進行總結、反思、梳理知識,中等生在一節課的時間內,基本可以完成作業;后進生也可以完成80%,可以說“四案”校本作業是普遍受到學生的歡迎,也是能有效激發學生學習數學的興趣和熱情的.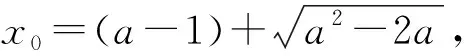

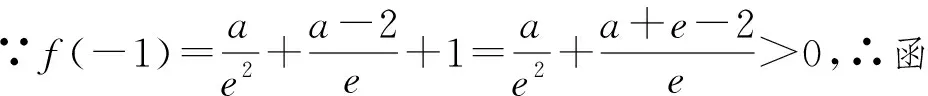


三、感悟

