考慮多主體主從博弈的多微網協調優化調度

練小林，李曉露，曹 陽，張 鴻，黃海峰

（1.上海電力大學電氣工程學院，上海 200090；2.中國電力科學研究院有限公司，南京 210003）

為了應對傳統能源枯竭、環境污染及氣候變化帶來的嚴峻挑戰，可再生能源得到迅速發展。微網作為一種容納分布式能源的重要組織形式，對電力系統安全運行有著重要作用[1]。隨著分布式能源滲透率的不斷提高，局部配電區域內將存在多個微網。多微網之間通過電能交互能夠有效促進分布式能源就地消納，提高系統運行穩定性[2]。

售電側電力體制改革的不斷推進使得擁有分布式能源的微網可以根據自身利益需求參與電能交易[3]。然而由于各微網屬于不同的利益主體，故不同微網的利益訴求不同。因此，如何在兼顧各方主體利益的前提下實現多微網協調運行是亟需解決的重要問題。

目前，眾多文獻已證明博弈論能夠有效解決多利益主體間的策略優化問題[4-5]。在與多微網協調優化相關的博弈方面，文獻[6]建立了配網和多微網之間的Stackelberg博弈模型，通過電價激勵增強微網間的電能交互。文獻[7]提出了基于合作博弈論的光伏微網群電能交易模型，降低了系統運行成本。然而，以上研究均忽視了微網的二重性，尚未從“源”、“荷”兩個角度出發，對多微網優化調度進行深入研究。

在充分考慮微網二重性的情況下，文獻[8-10]提出了基于雙向拍賣機制的多微網能量優化模型，通過雙向拍賣交易機制解決買賣雙方交易過程中的規則、秩序問題。文獻[11]通過采用合作博弈論及引入報價矩陣建立了買賣雙方多主體參與電能交易的競價機制，但未對多個買方及多個賣方之間的博弈問題進行研究。文獻[12]提出了基于多智能體的多微網電能交易策略，通過采用非合作博弈確定賣方的最優售電方案，但未考慮買方之間的博弈行為。文獻[13]充分考慮多主體間的博弈問題，提出了基于主從博弈的多微網電能交易模型，但僅適用于多微網供需平衡的情況，未考慮買賣雙方需求不等的情況。

針對以上問題，本文提出考慮多主體主從博弈的多微網協調優化模型。日前調度階段以微網運行成本最低為目標優化儲能充放電功率；實時調度階段通過建立多主體主從博弈模型研究多微網間電能交互問題。其創新性在于：①充分考慮微網二重性，建立了發電微網、用戶微網的多主多從博弈模型，并證明了該模型均衡解的存在性；②通過非合作博弈模擬發電微網之間價格競爭的同時，采用演化博弈求解多微網間電力消費行為策略；③采用二次效用函數描述微網的需求側滿意度大小，并分析其對多微網協調優化產生的影響。

1 多微網兩階段協調優化模型

綜合考慮可再生能源出力和負荷需求的波動性，本文的優化階段包括日前階段和實時階段。日前優化階段，根據可再生能源和負荷的日前預測數據，以微網運行成本最低為目標，優化儲能充放電功率；實時優化階段，基于儲能日前充放電計劃及可再生能源出力和負荷功率波動，通過構建多主體主從博弈模型，實時協調優化微網間的交互電能。

1.1 日前調度模型

1.1.1 目標函數

微網的運行成本主要包括儲能系統運行成本、負荷調度補償成本、微網間電能交易成本以及微網與配電網之間的電能交易成本，故日前調度的目標函數為

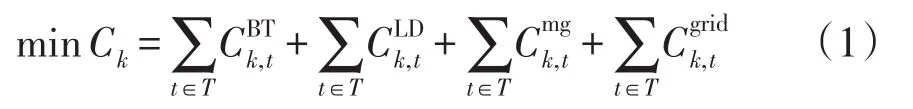
各成本的具體表達式如下：

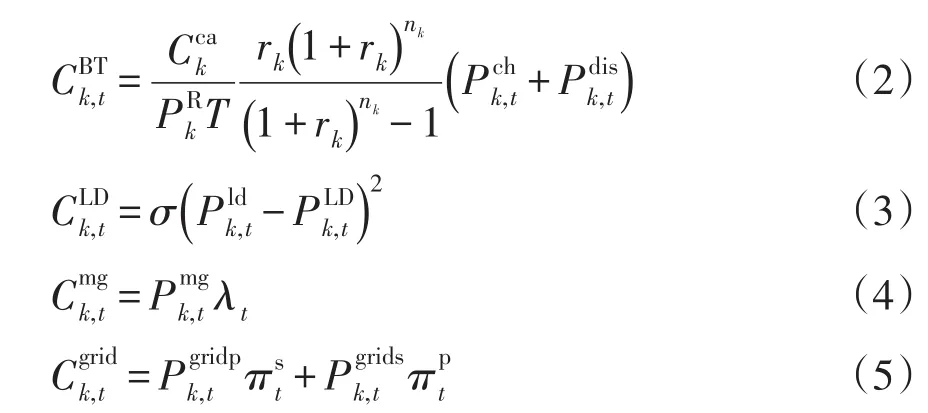
1.1.2 約束條件

1）功率平衡約束

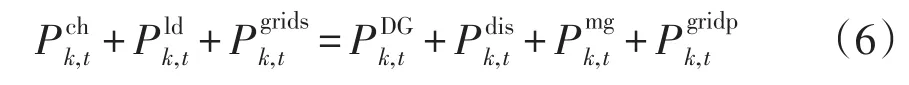
2）儲能電池運行約束

儲能電池的壽命與充放電深度密切相關，過充和過放都將加快電池的老化速度，故儲能系統應滿足以下約束。

儲能充放電功率約束為

此外，在同一時段，儲能系統不能即充電又放電，故還應滿足儲能充電功率和放電功率兩者乘積為零這一約束條件。

儲能容量約束為

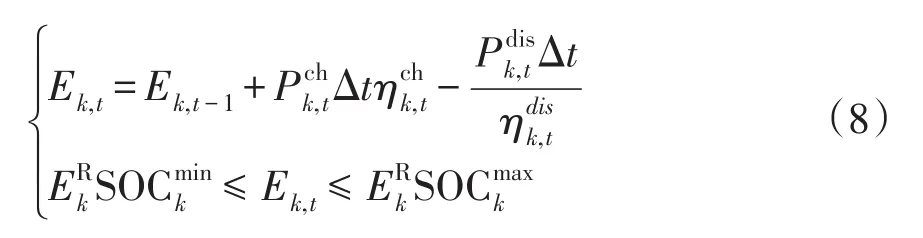
式中：Ek,t為t時段微網k儲能電池的電量；為微網k儲能系統的額定容量；為微網k儲能電池荷電狀態的最小值；分別為t時段微網k儲能的充、放電效率。

3）微網間交互功率約束

4）微網與配電網間交互功率約束

類似地，微網與配電網之間的交互功率也應滿足購電功率與售電功率兩者乘積為零這一約束。

1.2 實時多主體主從博弈模型

1.2.1 多主體主從博弈結構

實時調度階段，根據供需比系數SDR（supply-todemand ratio）[14]，將微網分為發電微網和用戶微網。

當SDRk,t＜1時，定義t時段的微網k為用戶微網，其集合用I表示；當SDRk,t＞1時，定義t時段的微網k為發電微網，其集合用J表示。

為了協調微網間電能交互，本文將發電微網與用戶微網之間的策略互動視為Stackelberg博弈過程，主方為發電微網，從方為用戶微網。博弈關系包括以下三種：①發電微網和用戶微網之間的Stackelberg主從博弈。發電微網以自身經濟最優發布電能價格，用戶微網根據價格信息做出最優選擇，并反饋給發電微網；②發電微網之間的非合作博弈。發電微網根據用戶微網的行為策略展開價格競爭，最終達到均衡狀態；③用戶微網的演化博弈。用戶微網之間通過演化博弈模擬行為演化。多主體主從博弈結構如圖1所示。

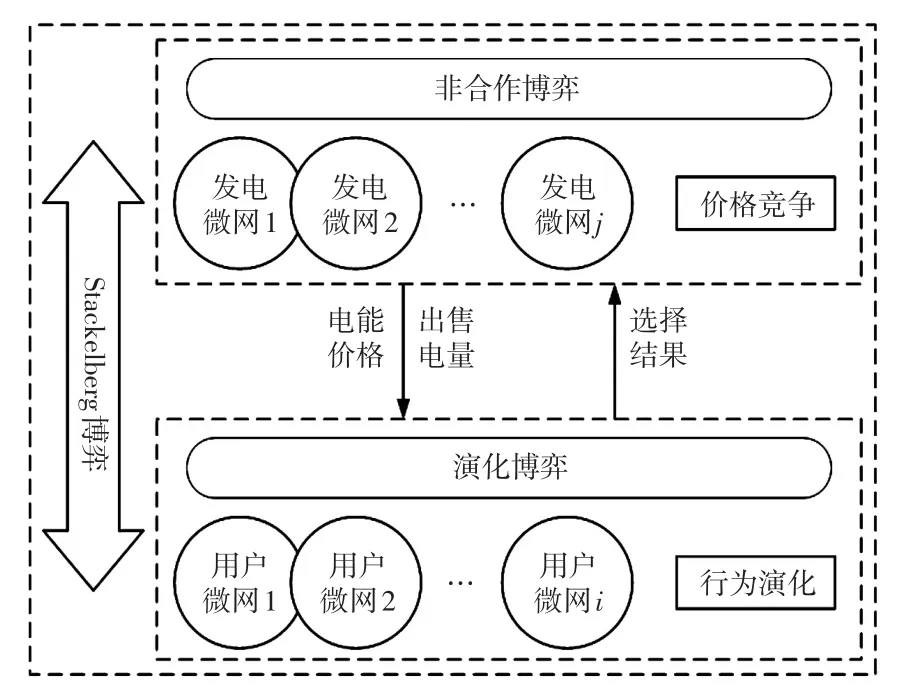
圖1 多主體主從博弈結構Fig.1 Multi-agent leader-follower game structure

1.2.2 微網效用函數

由于微網在各時段的供需特性不同，因此對于相同電價，其用電行為也不同。為了描述其用電行為偏好可以采用效用函數。此類效用函數主要包括對數效用函數和二次效用函數兩種[15]。由于此類函數關于用電量具有單調不減的特征，從而保證其具有線性邊際收益，可表示每個微網用電所帶來的滿意度大小。本文采用二次效用函數來描述微網需求側滿意度大小。

（1）用戶微網的效用函數。用戶微網由于電能供應量無法滿足負荷需求，需要購買電能以滿足供需平衡，其效用函數為

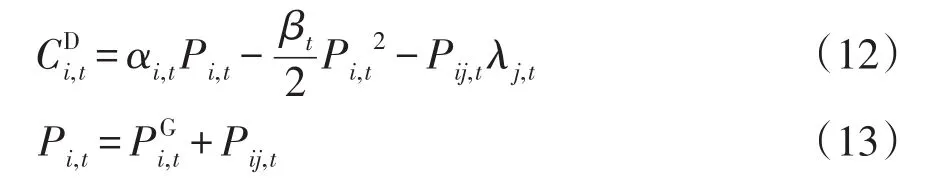
式中：αi,t為t時段用戶微網i的需求側滿意度系數；Pi,t為t時段用戶微網i實時優化后的負荷需求量；Pij,t為t時段用戶微網i與發電微網j之間的交易電量；βt為大于零的常數；λj,t為t時段發電微網j發布的電能價格。

用戶微網購買電能時存在以下約束：

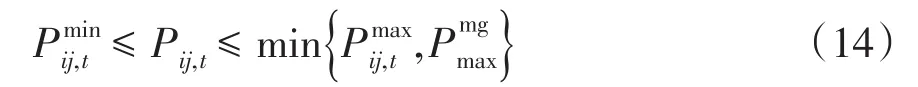
（2）發電微網的效用函數。發電微網通過出售過剩電能以提升經濟收益，其效用函數為

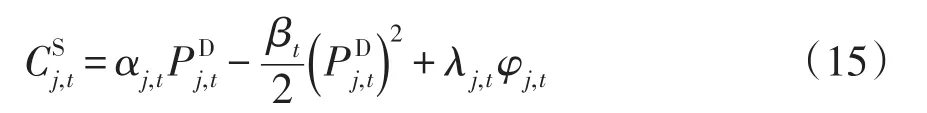
式中：αj,t為t時段發電微網j的需求側滿意度系數；為t時段發電微網j的實時負荷需求量；Pj,t為t時段發電微網j的過剩電量；Qj,t為t時段用戶微網從發電微網j購買的總電量；φj,t為t時段發電微網j的出售電量，φj,t=min( )Pj,t,Qj,t，φj,t應滿足以下約束：

1.2.3 多主體主從博弈均衡解的存在性

1）用戶微網的演化博弈

在演化博弈過程中，每個用戶微網根據發電微網發布的電能價格選擇一個發電微網購買電能，同時通過不斷學習和進化，根據歷史經驗來調整自身策略。經過一段時間，所有用戶微網最終會趨于某個穩定策略，從而達到演化均衡。

假設用戶微網在時段t選擇發電微網j購買電能的概率為ρj,t，且ρj,t滿足以下條件：

由式（12）可得，t時段用戶微網i的最優購買電量為

由此可得，t時段用戶微網需要從發電微網j購買的總電量為

考慮到發電微網j自身的過剩電量可能不足以滿足所有用戶微網的購電需求，故t時段用戶微網i與發電微網j之間的實際電能交易量為

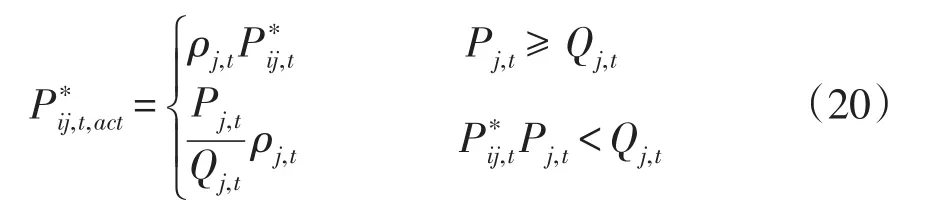
兩種情況下，t時段發電微網j可獲得的效用?j,t可表示為

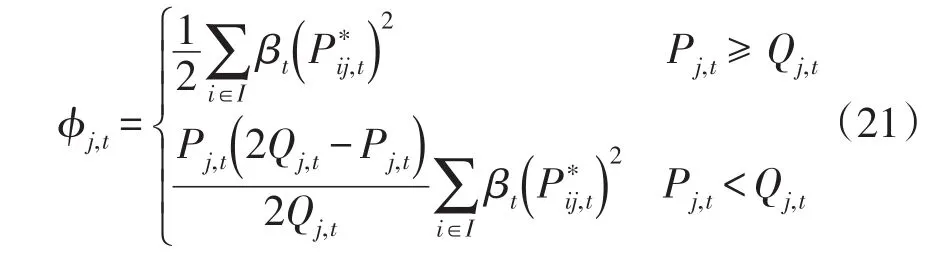
在演化博弈過程中，用戶微網基于各策略適應度不斷對策略進行選擇和進化，故各種策略的概率會發生動態變化。博弈演化的復制動態可描述為

為了獲得博弈的演化均衡策略，需求解式（22）的穩定奇點，即

2）發電微網的非合作博弈

為了求解發電微網的非合作博弈模型，需要尋找納什均衡點。根據納什均衡點存在性定理：在有限個參與人的博弈問題中，若參與人的策略集合是閉的、有界的凸子集，且策略空間上的每一個效用函數是擬凹和連續的，則該博弈問題存在納什均衡點。

在發電微網的非合作博弈中，參與人是發電微網，電能價格是發電微網的策略。發電微網的效用函數為

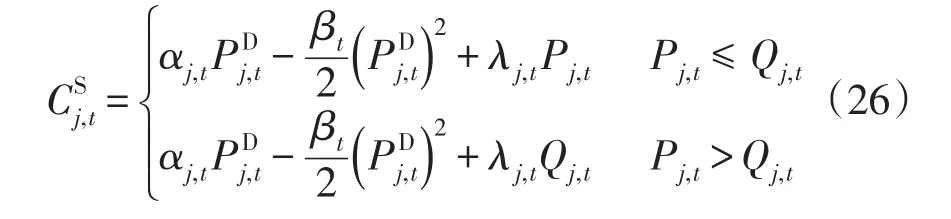
式中，發電微網的個數為j個，即博弈的參與人是有限的。電能價格。因此，j個發電微網的價格策略集合是閉的、有界的凸子集，且當發電微網j參與電能交易時必然有對應的價格策略存在，故策略集合非空。

此外，由式（19）可知，用戶微網的總購電需求為

將式（27）代入式（26）可得發電微網的效用函數為

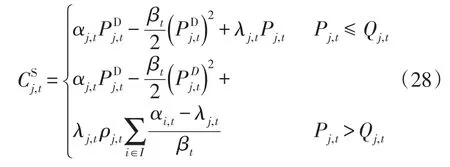
3）發電微網和用戶微網之間的Stackelberg博弈

在發電微網和用戶微網之間策略互動形成的Stackelberg博弈中，當發電微網通過非合作博弈發布電能價格時，用戶微網根據所得價格信息進行動態演化以達到演化均衡。由上述可知，非合作博弈存在均衡解，同時演化博弈的收斂性已得到保證。因此，通過重復上述過程可獲得微網間電能交互策略，即Stackelberg博弈存在均衡解。

2 模型求解

2.1 日前調度模型求解

本文選取改進的粒子群優化算法對日前調度模型進行求解。相比于標準粒子群算法，本文選取的改進粒子群算法引入了模擬退火思想。通過利用模擬退火算法在一定概率控制下能夠接受一些劣質解的特性，克服標準粒子群算法易陷入局部最優的弊端，改善算法的收斂性能。日前調度模型的求解流程如圖2所示，具體步驟如下：

步驟1輸入基礎數據（可再生能源出力、負荷需求、儲能數據等）；

步驟2初始化粒子群算法的相關參數（粒子的個數、迭代次數及粒子的速度和位置）；

步驟3設置模擬退火的初始溫度，計算個體最優解和全局最優解；

步驟4更新粒子的速度和位置，并計算每個粒子的適應度值；

步驟5為粒子隨機產生一個新位置，判斷新舊 位 置 的 適 應 度 之 差 ΔC。 若 ΔC＜0或exp(- ΔC∕T) ΔC＞rand(0 ,1)，粒子進入新位置；否則根據當前速度和位置計算粒子適應度值；

步驟6更新個體最優解和全局最優解；

步驟7判斷是否滿足終止條件。若滿足條件，則執行步驟8，若不滿足條件，則跳到步驟4；

步驟8輸出優化結果。

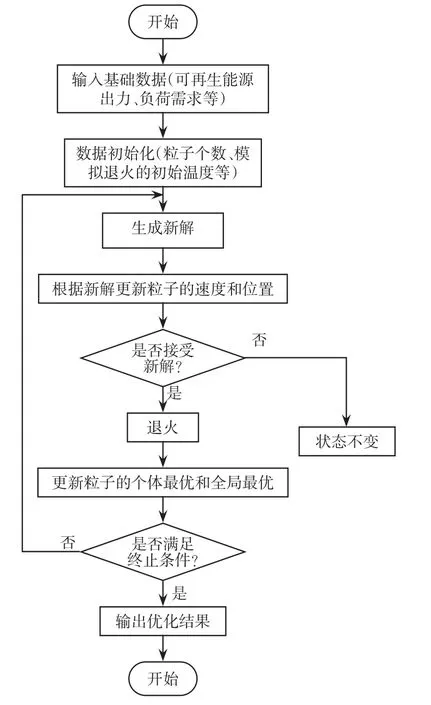
圖2 日前調度模型的求解流程Fig.2 Flow chart of day-ahead scheduling model solving

2.2 實時博弈模型求解

在求解實時博弈模型時，用戶微網首先根據發電微網發布的電能價格確定最優行為策略，然后發電微網根據用戶微網的行為策略調整電能價格，并反饋給用戶微網，最終通過多回合博弈求得主從博弈均衡解。求解流程如圖3所示。

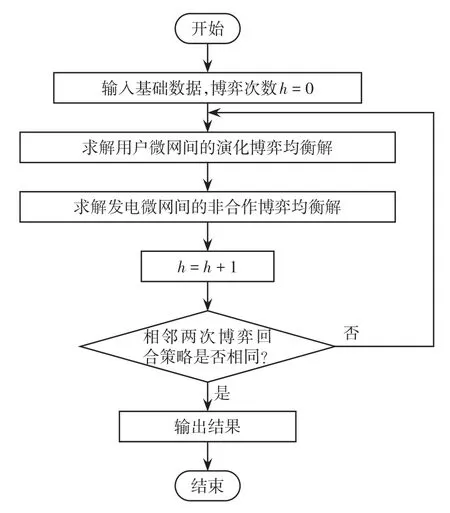
圖3 實時博弈模型的求解流程Fig.3 Flow chart of real-time game model solving

其中，發電微網的非合作博弈均衡解求解過程和用戶微網的演化博弈均衡解求解過程如下。

（1）初始化電能價格，令非合作博弈迭代次數n=1。

（2）根據演化博弈均衡解，發電微網可獲得用戶微網的總購電需求。

（3）發電微網根據式（29）計算自身價格更新策略為

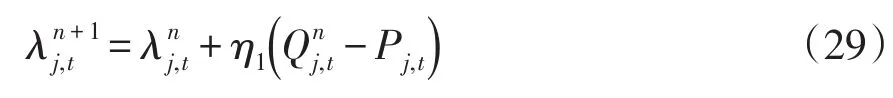
式中，η1為步長因子。

（4）令n=n+1，重復上述步驟，直至滿足以下條件。

式中，ε1為允許誤差。

用戶微網的演化博弈求解過程如下。

（1）數據初始化，令演化博弈迭代次數m=1。

（2）根據發電微網發布的電能價格，每個用戶微網選擇一個發電微網j購買電能，并計算發電微網j的效用和平均效用值。

（3）根據式（31）更新用戶微網的演化行為策略為

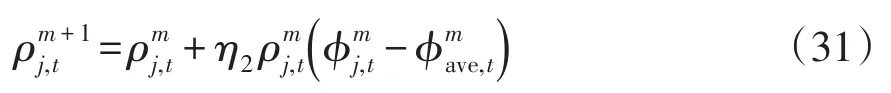
式中，η2為步長因子。

（4）令m=m+1，重復上述步驟，直至滿足以下條件。

式中，ε2為允許誤差。

3 算例分析

3.1 基礎數據

本文選取 5個互聯微網（MG1、MG2、MG3、MG4、MG5）進行仿真分析。各微網的可再生能源出力預測曲線如圖4所示，實時出力的波動范圍為預測出力的90%～110%；負荷需求預測曲線如圖5所示，實時需求的波動范圍為預測負荷需求的95%～105%。儲能系統的額定容量為300 kW·h，最大允許充放電功率為100 kW，充放電效率均為0.9，折舊率取0.005元∕kW2。配電網購售電價如表1，微網間日前交易電價的制定見文獻[16]。微網需求側滿意度系數的取值范圍為[5，10]，β取值0.5。算例調度周期取一天，以1 h為步長將一天分為24個時段選擇調度時間段為當日零點至次日零點。

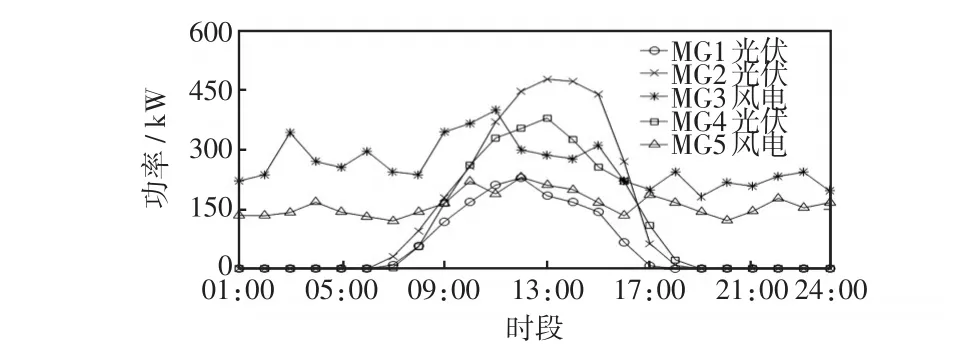
圖4 可再生能源出力預測曲線Fig.4 Forecasting curves of renewable energy output

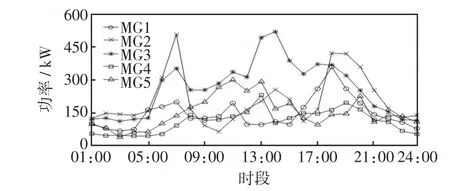
圖5 負荷需求預測曲線Fig.5 Forecasting curves of load demand

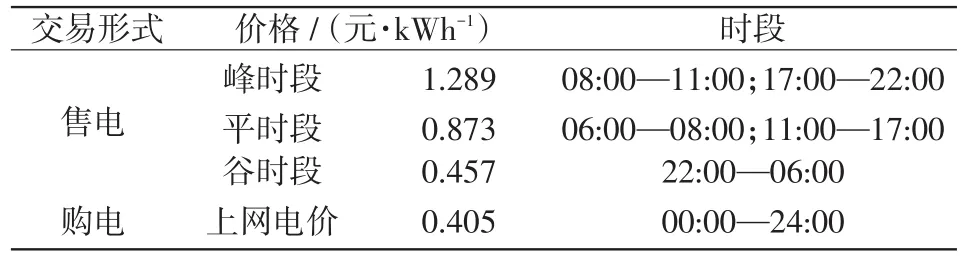
表1 分時電價Tab.1 TOU electricity rates

3.2 優化結果分析

3.2.1 日前優化結果

1）日前儲能優化結果

儲能的日前充放電功率優化結果如圖6所示。

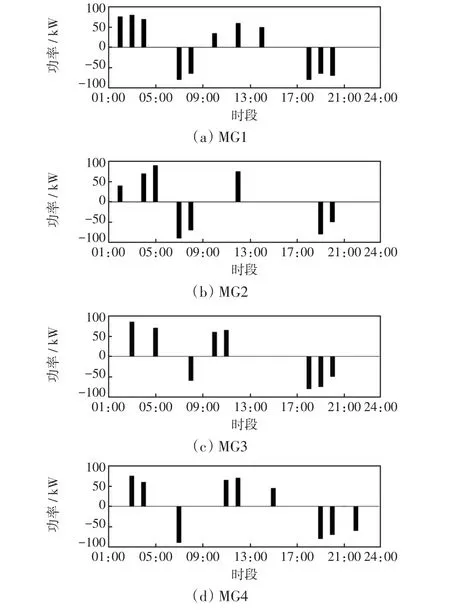
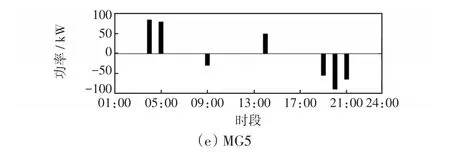
圖6 儲能日前充放電功率Fig.6 Day-ahead charge and discharge power of energy storage

從圖6可以看出，在時段1:00—6:00，各微網的儲能系統僅充電不放電，從而將谷電價時段的電能存儲起來，滿足平時段和峰時段的負荷需求。在時段10:00—17:00，儲能通過繼續充電來消納本地過剩可再生能源，以滿足晚高峰時段的負荷需求增長。在時段18:00—22:00，MG1、MG2和MG4的儲能放電以滿足由于可再生能源出力不足造成的電能短缺。MG3和MG5的儲能放電功率在滿足自身負荷需求的同時，通過將電能出售給其他微網來促進系統供需平衡，提高經濟效用。

3.2.2 實時優化結果

實時優化結果將以時段3（MG1、MG2和MG4為用戶微網，MG3和MG5為發電微網）為例，從模型收斂性、發電微網的經濟效益和可再生能源出力預測偏差的影響三個方面進行分析。

（1）模型收斂性。用戶微網購買電能的概率收斂過程和發電微網電能價格的收斂過程如圖7與圖8所示。用戶微網電量需求的收斂過程如圖9所示。

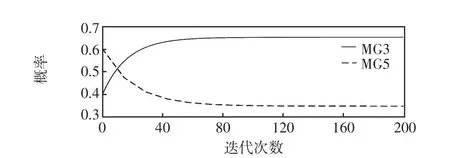
圖7 用戶微網購買電能的概率收斂過程Fig.7 Probability convergence process of electricity purchased by user-microgrid

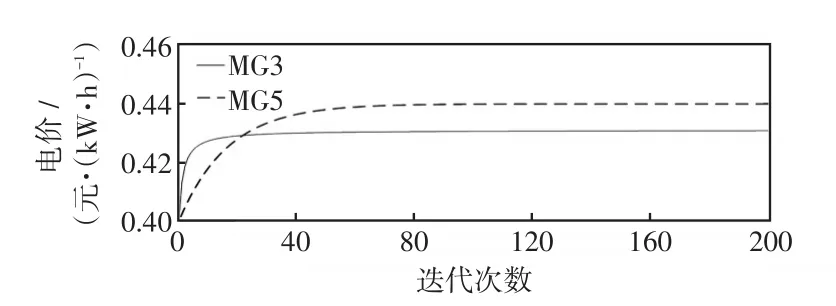
圖8 發電微網電能價格的收斂過程Fig.8 Convergence process of generator-microgrid’electricity price

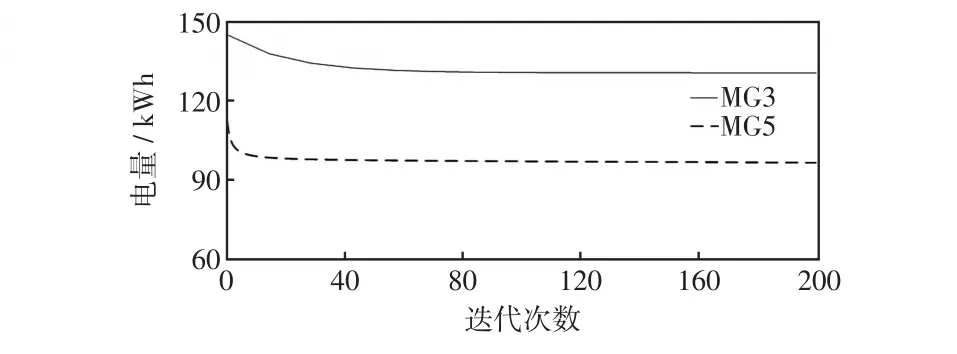
圖9 用戶微網電量需求的收斂過程Fig.9 Convergence process of user-microgrid’electricity demand

由圖7可知，用戶微網從發電微網購買電能的概率能夠快速收斂到均衡值，即用戶微網的動態行為達到演化均衡。由圖8可知，發電微網的售電電價最終收斂到了一個固定值，此時發電微網之間的非合作價格競爭達到均衡，與演化均衡一起，構成用戶微網和發電微網之間的主從博弈均衡。由此驗證了實時博弈模型的收斂性。通過比較圖8與圖9可以發現，當發電微網的售電電價增加時，用戶微網的電量需求呈下降趨勢，與微網實際電力消費行為保持一致。

（2）發電微網的經濟效益。為了分析發電微網之間進行博弈對其經濟效益的影響，將發電微網間無博弈和有博弈兩種情況下的經濟效益進行了對比，如圖10所示。從圖中可以看出，相比于發電微網間無博弈的情況，發電微網間有博弈時的經濟效益更高。當計及發電微網間的博弈時，發電微網享有議價權，即其電能價格不再是日前售電電價，而是能夠根據自身利益對電能價格進行優化，故發電微網間進行博弈對提升系統經濟性有著促進作用。

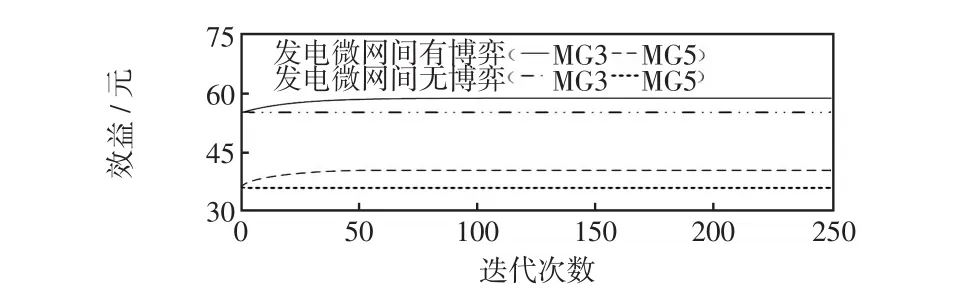
圖10 發電微網的經濟效益Fig.10 Economic profits of generator-microgrid

（3）可再生能源出力預測偏差的影響。為了探究風光出力預測偏差對主從博弈造成的影響，給出了不同預測偏差下主從博弈的迭代次數，如圖11所示。

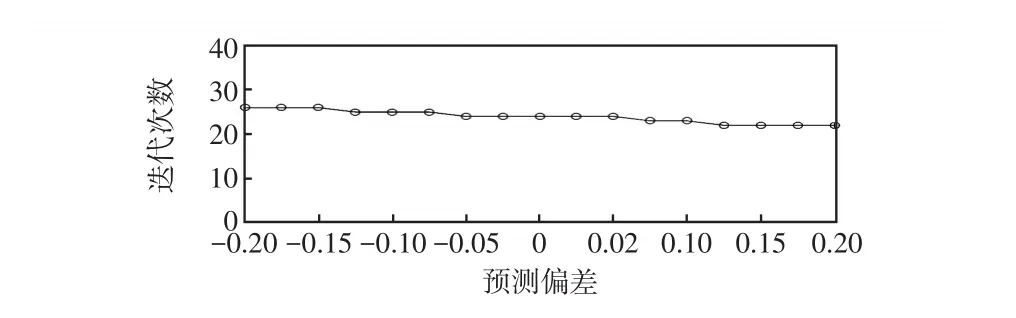
圖11 不同預測偏差下主從博弈的迭代次數Fig.11 Iteration numbers of leader-follower game with different prediction deviations

從圖11可以看出，風光出力預測偏差與主從博弈迭代次數之間的關系曲線變化非常平緩。當預測偏差為0時，用戶微網的總需求電量大于發電微網的總供應電量。在預測偏差從0增大至0.2的過程中，用戶微網的總需求電量逐漸減小，發電微網的總供應電量逐漸增大，從而使得兩者之間的差值逐漸變小，此時迭代次數略微減小。反之，在預測偏差從0減小至-0.2的過程中，用戶微網的總需求電量逐漸增大，發電微網的總供應電量逐漸減小，從而使得兩者之間的差值逐漸變大，此時迭代次數略微增加。但是預測偏差的變化并未對主從博弈迭代次數產生過多影響。在下一步的工作中，將針對大規模互聯微網，深入探究可再生能源出力不確定性對微網間主從博弈的影響。

3.2.3 對比分析

為了驗證所提模型的有效性和經濟性，將以下調度策略進行對比分析：策略1以微網經濟性為目標，微網間無電能交互且不考慮需求側負荷同時不計及需求側滿意度；策略2在策略1的基礎上考慮微網間電能交互；策略3在策略2的基礎上考慮需求側負荷同時計及需求側滿意度（本文模型）。下面將從微網與配電網之間的電能交互和微網經濟性兩個方面進行分析。

（1）微網與配電網之間的電能交互結果分析。MG1與配電網之間的電能交互結果如圖12所示，其余微網的仿真結果如圖13。

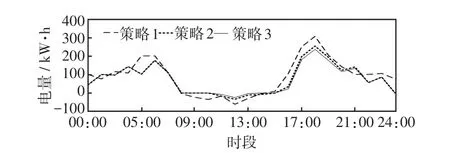
圖12 微網MG1與配電網之間的電能交互Fig.12 Electricity interactions between microgrid MG1 and distribution network

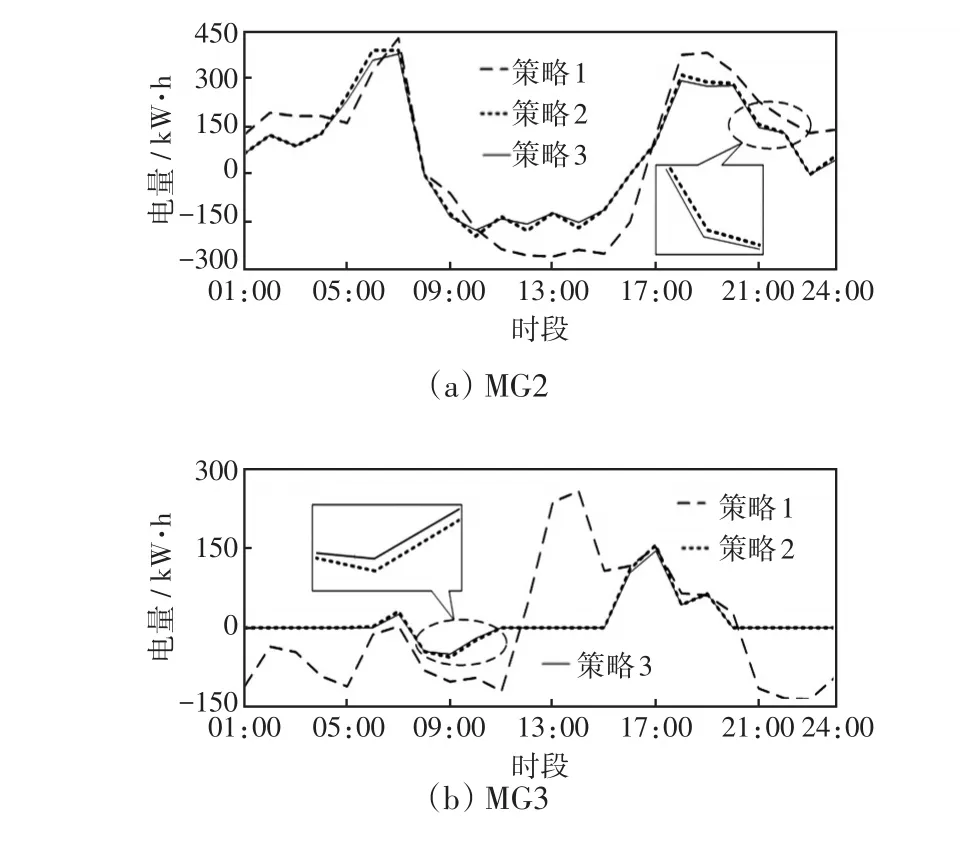
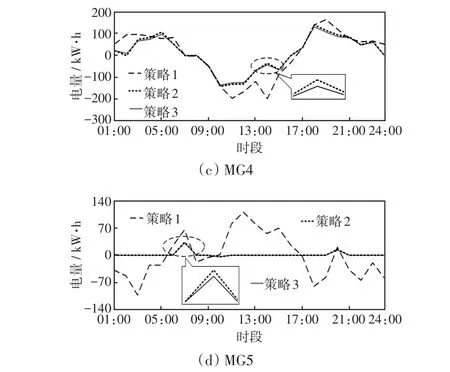
圖13 其余微網與配電網之間的電能交互Fig.13 Electricity interactions between the others microgrids and distribution network

從圖12可以看出，相比于策略1，在策略2和策略3下MG1與配電網間的交易電量均明顯減小。當計及微網間電能交互時，在市場均衡的情況下，MG1可以向其他微網購買或出售電能，從而有效減小微網與配電網之間的交易電量，降低多微網接入給配電網造成的影響。此外，通過比較策略2和策略3可以發現，在時段11：00—14：00和時段16：00—21：00，策略3下MG1與配電網之間的交易電量有所減小。該現象表明，需求側負荷能夠有效促進微網間電能交互，充分消納過剩可再生能源。

（2）微網經濟性。三種策略下微網的運行成本如表2所示。由此可得，策略1下各微網的運行成本最高，策略3下各微網的經濟性最優。由于微網間的電能交易價格介于配電網的購售電價之間，故通過促進微網間電能交互能夠明顯提升系統經濟效用。以MG1為例，相比于策略1，策略2下MG1的運行成本降低了7.6%；相比于策略2，策略3下MG1的運行成本降低了1.8%。對多微網系統而言，三種策略下多微網系統的總運行成本依次降低10.8%和2.3%，提高了系統運行經濟性。

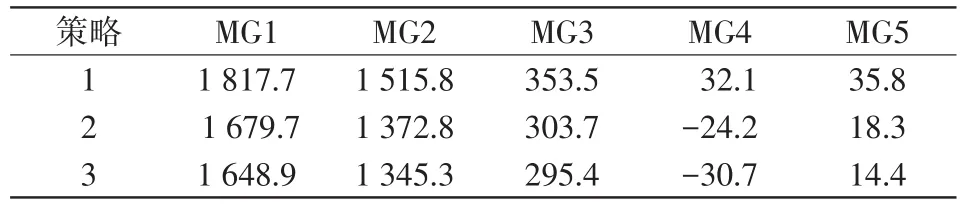
表2 微網的運行成本Tab.2 Operating costs of microgrids元

4 結論

本文提出了考慮多主體主從博弈的多微網協調優化模型，并驗證了博弈模型的收斂性，以及對比分析了不同調度策略下的優化結果，最終得出以下結論：

（1）實時博弈階段可以較快地在發電微網和用戶微網之間形成基于動態定價的電能交易策略，提高系統經濟效益，促進系統供需平衡；

（2）所提模型通過日前和實時兩階段協調優化減小了可再生能源出力波動性對系統造成的影響。

此外，通過計及微網間電能交互及需求側負荷實現了可再生能源的充分消納，降低了多微網對配電網的依賴性，確保了系統安全穩定經濟運行。