催化裂化中可壓縮湍流氣固兩相數值模擬

周迪鋒，劉冬玉

(1.上海儀器儀表自控系統檢驗測試所有限公司，上海 200233；2.浙江工業大學 機械工程學院，浙江 杭州 310014)

引言

催化裂化是將重油深度加工生產高辛烷值汽油、柴油、液化石油氣等高附加值產品的石油煉制過程，催化裂化裝置的長周期安全穩定運行一直是煉油工業所追求的目標[1]。

催化裂化裝置的活力是靠流化態的催化劑顆粒循環。催化劑是粒徑20～100 μm的固體球形顆粒，主要成分是氧化鋁。催化劑在整個裝置中都處于流化狀態，通過氣流的輸送實現循環流動。由于大量催化劑在催化裂化裝置中高速流動和多次循環，使得裝置中的許多構件工作在高溫、大量固體顆粒不斷沖刷、撞擊的環境下，會引發2方面的問題：一方面高速運動的催化劑顆粒在循環過程中，經過一些部位時線速度過高，對管壁的撞擊引起催化劑顆粒的破碎,使價格昂貴的催化劑大量跑損，同時催化劑顆粒減少會使裝置的流化質量惡化，對催化裂化反應有很大影響[2-3]；另一方面由于催化劑顆粒的撞擊與沖刷，造成催化裂化裝置中的諸多構件沖蝕磨損,對裝置的長期運行產生直接威脅，這是造成設備停工停產的最主要原因之一[4]。

為了使催化裂化高效進行，裝置內氣流的設置顯得十分重要。在裝置中，氣流處于湍流狀態，氣固兩相可壓縮氣體的湍流問題是流固耦合領域中公認的難題之一，而湍流流動又是自然界和工程中廣泛存在的現象，因此很多研究人員在這個領域做了大量的工作。尤其是在20世紀90年代，大渦模擬亞格子模型蓬勃發展，可壓縮湍流的研究取得了巨大的進步。LARCHEVEQUE等[5]推導了可壓縮LES的控制方程；GERMANO等[6]提出的動力渦粘模型開創了LES應用于實際工程問題計算的先例；ELGHOBASHI[7]研究了應用LES解決多種幾何形狀的氣固兩相流動。

催化裂化過程的核心步驟是原油在催化劑的作用下反應，這個步驟在沉降塔內完成。沉降塔是由圓柱直筒構成的，簡化沉降塔，用一個圓柱形流道代替。分析流道中的氣場和催化劑的運動特征，采用PFC-CCFD耦合的仿真方式，取代Fluent仿真方法，來觀察流道中的每個催化劑的運動狀態，并且通過PIV觀測裝置驗證顆粒撞擊壁面。

1 兩相流控制方程

可壓縮湍流的LES控制方程通過可壓縮N-S方程Favre過濾得到：

(1)

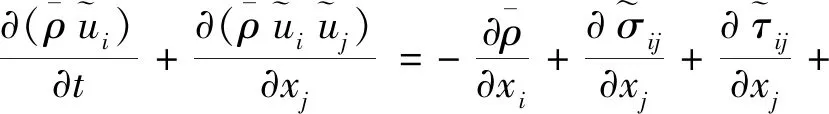
(2)

(3)

式中，“-”——物理空間過濾

“～”——密度加權過濾

ρ——密度

ui，uj——速度分量

xi，xj——坐標

p——壓力

σij——黏性應力項

E——總能量

qj——熱通量

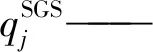
其中：

(4)

(5)

(6)

(7)

式中,Cs——Smagorinsky常數

λ——比熱

T——溫度

μ——動力黏度

2 顆粒流數值模擬

在催化裂化裝置的管道中，流場是由氣化狀態的原油構成的，固體是催化劑顆粒，參數如表1所示，流場的管道用圓柱筒代替，尺寸如圖1和表2所示。氣固耦合數值仿真采用結合離散單元法[9-10]和計算流體動力學的方法[11-12]，用PFC3D和CCFD分別來仿真催化劑顆粒和氣場，流道網格如圖2所示。

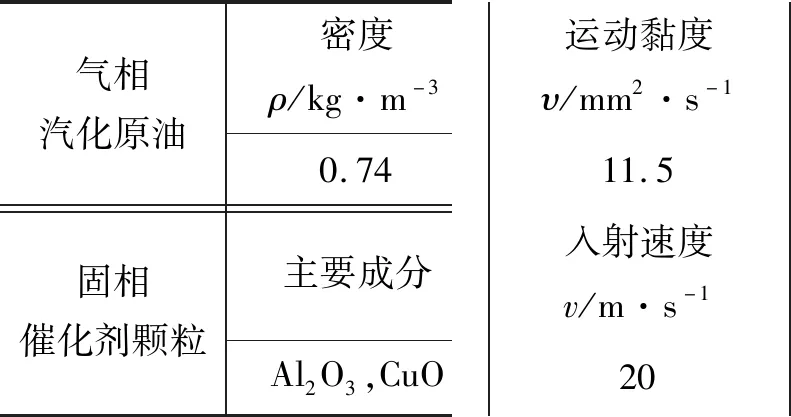
表1 物理特性參數

表2 流道尺寸參數 mm

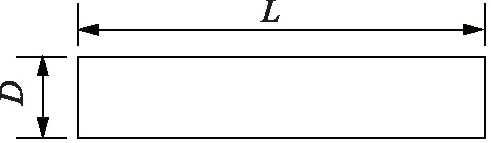
圖1 流道尺寸

圖2 流道網格

雷諾數方程為：

Re=vD/υ

(8)

式中,Re——雷諾數

v——速度

υ——運動黏度

得到Re=6956，按照雷諾數與流體運動狀態的關系可知，此參數條件下氣場處于湍流狀態。

在PFC-CCFD的數值模擬中，在氣場中加入了1000顆催化劑顆粒，氣場和顆粒的初始速度是 20 m/s。

3 計算結果分析

3.1 曳力的分布

曳力是表示氣固兩相的相互作用和動量傳遞的重要參數，曳力大小決定了氣流對于催化劑顆粒的運動影響[13]。

曳力的分布采用Wen&Yu模型：

Fdrag=Fden+Fint

(9)

式中，Fdrag——曳力

Fden——顆粒密相的曳力

Fint——顆粒相互作用相的曳力

其中：

Fint=βintuf

(10)

Fden=εpβdenuc

(11)

式中，εp——顆粒的體積分數

uc——氣流穿過顆粒的速度

uf——氣流繞過顆粒的速度

βint，βden——曳力函數

其中，βint，βden的值可以由Wen&Yu[11]模型給出：

(12)

(13)

式中,μg——氣體的動力黏度

εmax——顆粒的最大體積分數

ρg——氣體的密度

d——顆粒的直徑

l——流道長度

Cl——尺度因子

曳力的分布如圖3所示。

圖3 曳力的分布

3.2 氣流速度分布

曳力是氣流作用在催化劑顆粒上的力，同時氣流受到一個同樣大小的反作用力，因此氣流速度的大小應該與曳力大小的分布相反，即曳力越大，氣流速度越小，曳力越小，氣流速度越大。對比圖3、圖4印證了這一論點。

圖4 氣流速度分布

3.3 顆粒速度分布

催化劑的跑損主要是由于2方面引起的，一是催化劑顆粒與管壁的撞擊，二是催化劑顆粒與催化劑顆粒的撞擊。因此求得顆粒撞擊管壁的速度及顆粒與顆粒撞擊的速度是仿真的關鍵。

在PFC-CCFD仿真中，1000個催化劑顆粒共發生了2309次撞擊，其中顆粒和顆粒撞擊1653次，顆粒和管壁撞擊656次，平均每個顆粒發生2.3次撞擊。所有顆粒中撞擊次數最多的是8次，最少的則沒有撞擊。

催化劑顆粒撞擊速度vh分布比例如圖5所示，顆粒賦予水平方向的初速度20 m/s，撞擊速度大部分分布在18～20 m/s之間，由于顆粒之間的撞擊作用，顆粒獲得了其它方向的速度，所以顆粒的速度有可能大于初速度。大于20 m/s的撞擊速度對于催化劑的使用壽命有很大的影響。

圖5 催化劑顆粒撞擊的速度分布

催化劑顆粒的總動能如圖6所示，觀察到顆粒總動能走向趨勢大致可以分為3段：第1段是穩中有升，此時撞擊發生次數較少，顆粒的速度基本不變，曳力也較小；第2段是快速下降段，此時是撞擊發生的高峰期，有碰撞就會有動能的損失，此時的曳力也最大；第3段是趨于上升段，顆粒在出流道口趨于穩定，撞擊次數減少，曳力使得動能變大。

圖6 顆粒總動能隨時間步的分布

顆粒在管道中軌跡如圖7所示，從圖中可以看到顆粒在管道中的運動軌跡，顆粒就發生一次碰撞，軌跡線就發生一次轉折。

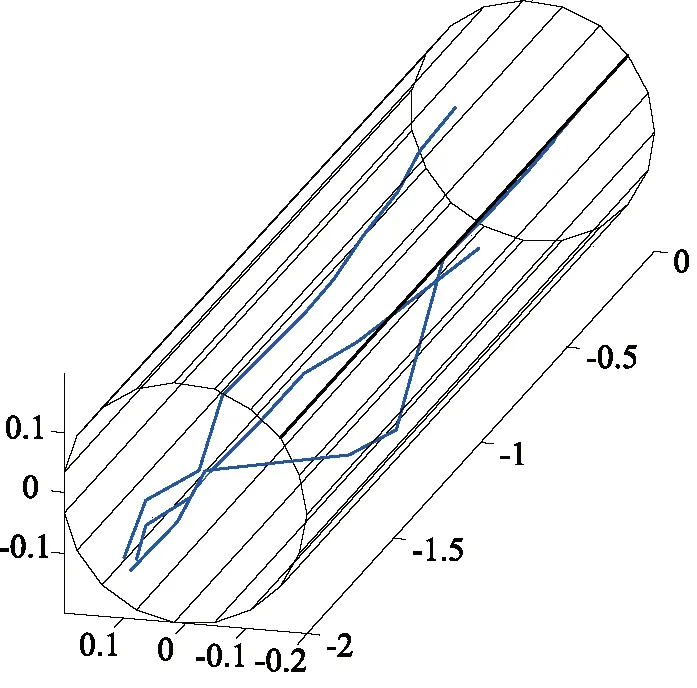
圖7 顆粒軌跡圖

3.4 撞擊速度對顆粒磨損的影響

催化劑顆粒的撞擊速度是影響催化劑使用壽命的最重要原因，撞擊速度大引起顆粒較大的磨損，使得使用壽命下降。當催化劑分別以10，15，20，25 m/s的速度和壁面發生撞擊時，圖8為顆粒的質量損失Δm與撞擊vh速度的關系。當撞擊速度小于10 m/s時，基本沒有質量損失；當速度為15～20 m/s時，質量損失較小；當速度大于20 m/s，隨著速度的增加質量損失迅速變大。表3為壁面材料屬性和催化劑材料屬性。

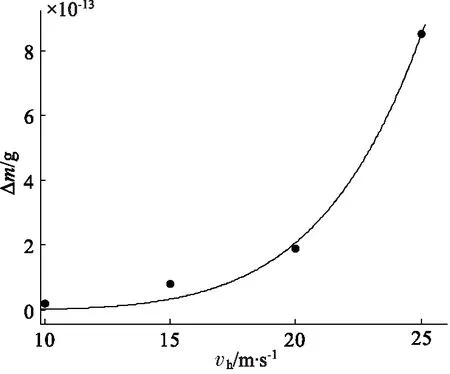
圖8 撞擊速度與顆粒質量損失關系

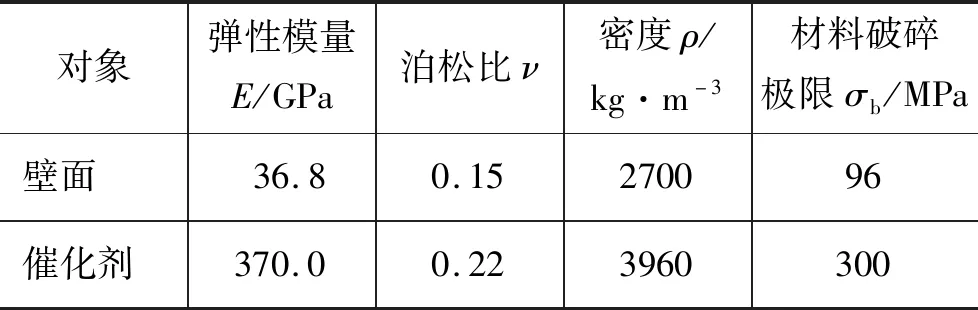
表3 材料屬性

3.5 PIV觀測實驗

設計了催化劑撞擊壁面的觀測實驗，選用陽離子交換樹脂作為示蹤粒子，顆粒直徑在0.6～0.8 mm，用泵將顆粒流以20 m/s的速度輸入流道中，采用PIV觀測系統，觀察顆粒的運動和湍流運動，顆粒撞擊壁面過程如圖9所示。

圖9 顆粒撞擊壁面過程

雖然經典流體力學中流體在壁面的速度為0，但是顆粒由于受到湍流、曳力、顆粒間撞擊的作用，使得顆粒也會撞擊壁面。

圖10是管道中湍流渦量圖。

圖10 湍流渦量

4 結論

本研究基于LES湍流模型，分析了圓柱流道內氣固兩相流動力學特性。通過理論分析、數值模擬和實驗研究，可以得到以下結論：

(1) 曳力的分布與氣流速度分布正好相反，曳力越大，氣流速度越小；

(2) 曳力大小與催化劑總動能相反，曳力越大，催化劑總動能越小；

(3) 催化劑顆粒的速度對催化劑的質量損失有很大影響，超過20 m/s的撞擊速度會引起較大的質量損失；

(4) PIV試驗得到催化劑顆粒在多個作用力下，顆粒會與壁面發生碰撞。