基于性能的大跨橋梁顫抖振響應概率性評價

邵亞會, 海 瑞, 鐘 劍, 趙 彤

(合肥工業大學 土木與水利工程學院,安徽 合肥 230009)

0 引 言

結構抗震在基于概率的基礎上進行的性能研究目前已基本形成較為完善的體系。橋梁抗風因其復雜性和隨機性,目前主要研究仍然集中在風致振動機理的研究。文獻[1]提出基于結構性能的抗風方法(performance-bsed wind engineering,PBWE),目前仍處于初步發展階段;文獻[2-3]將基于性能的抗震設計方法引入PBWE,分別采用Monte Carlo法和子空間模擬法對某人行天橋進行基于性能的抗風設計評估;文獻[4-5]采用PBWE方法對懸索橋的吊桿和海上風力發電機組進行了設計和研究;文獻[6]根據我國大陸地區風壓分布特點建立了PBWE理論框架,總結出適應于我國的多級設計風壓值、多級抗風性能水準和多級抗風性能目標;文獻[7]以基于概率性能的抗震設計理論為基礎,建立基于性能的結構抗風設計概率評估框架;文獻[8]對薄膜結構的抗風性能進行了概率性的評估,提出薄膜屋蓋結構抗風性能概率評估框架。

橋梁的顫抖振響應是橋梁抗風性能研究的重要組成部分,其機理與研究方法也已成熟。現階段對顫抖振的研究多是定量的,忽略了風場的隨機性對顫抖振計算的影響,必然會導致計算結果的偶然性。為確定顫抖振對結構的影響,本文將PBWE方法引入到大跨度橋梁的顫抖振響應的分析中,以江陰長江大橋為例,借鑒美國太平洋地震工程研究中心基于性能的抗震設計方法,考慮風場的隨機性,依據規范譜對該橋所處風場進行了模擬,進行了顫抖振響應計算;擬合出該橋不同風速下的最不利部位最大響應曲線;通過對相同風速下多組橋梁跨中加速度響應的分析,代表性提出用正太分布來擬合最不利部位的概率密度,并對該假設進行了驗證。基于行車和行人舒適度標準,確定了不同損傷程度的界限,建立了大跨橋梁基于舒適度標準的四級損傷評價標準。對江陰大橋進行分析,計算不同損傷級別下該橋梁最不利部位的損傷概率,通過擬合得到了結構的損傷曲線,為橋梁損傷程度的判斷提供了依據。

1 風場模擬與顫抖振分析

1.1 脈動風速場的模擬

依據文獻[9],脈動風速在橫向和豎向分別采用Davenport譜和Kaimal譜模擬。

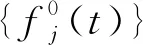
θjm(ωml)+φml)

(1)

對文獻[11]中江陰長江大橋橋位所在處進行風場模擬,主梁模擬點數為85,各點等間隔分布,點間距為16 m,頻率等分點數為1 024,采樣時距取0.1,不考慮導納函數修正。橋面平均風速為40 m/s時,主梁跨中節點10 min的風速時程如圖1所示。

(a) 橫向

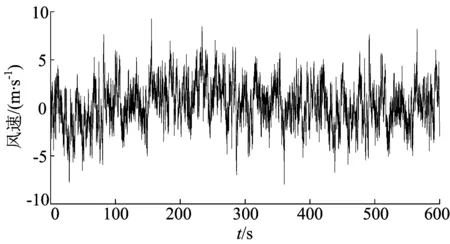
(b) 豎向圖2 跨中節點橫向和豎向風速時程

1.2 顫抖振響應分析

抖振是指自然風中的脈動成分引起的隨機性強迫振動,現階段對抖振的計算是針對大氣邊界層特征紊流引起的結構抖振。在有限元分析中,橋梁結構在空氣中運動的控制方程可表示成如下的一般形式:

(2)

其中:M、C、K分別為結構質量、阻尼和剛度矩陣;Fb為等效節點抖振力向量;Fse為等效節點的氣動自激力[12]。

通過同濟大學風洞實驗室得到江陰大橋主梁斷面三分力系數CD、CL、CM與顫振導數H*、A*如圖2、圖3所示。

本文對江陰大橋進行了多風速下顫抖振的時程分析[13],當橋面平均風速為40m/s時跨中加速度時程如圖4所示。

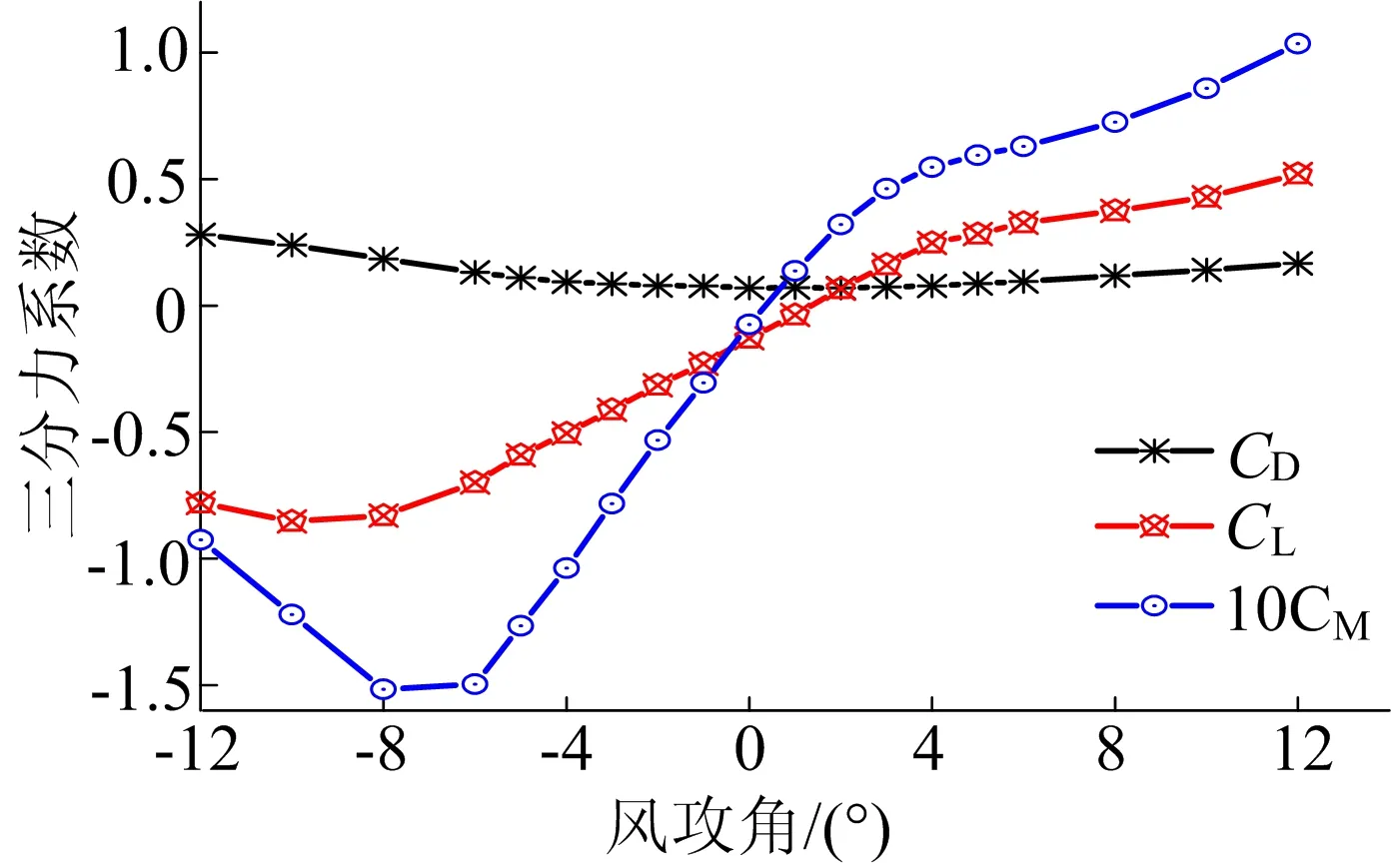
圖2 主梁斷面靜風力系數

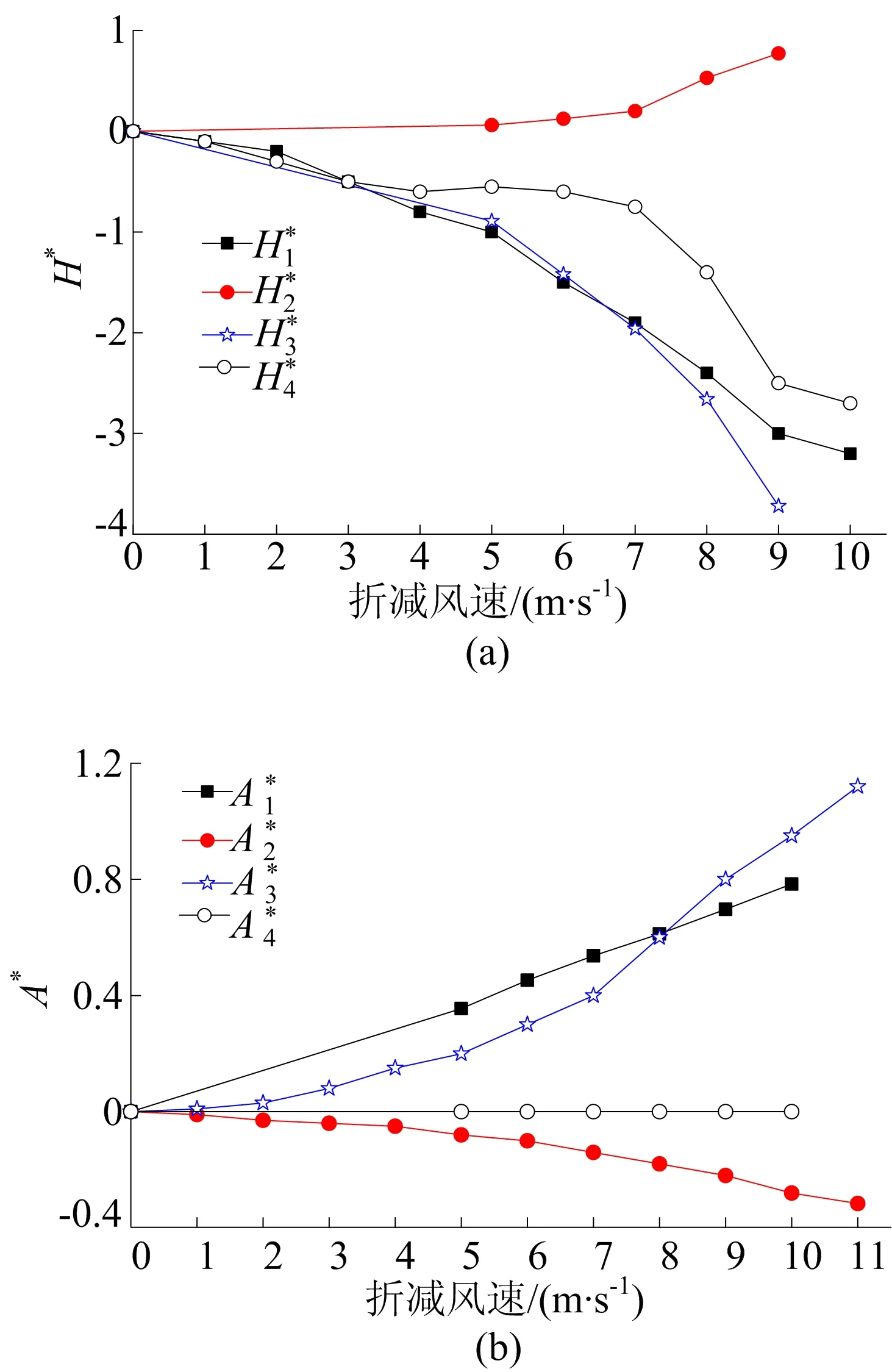
圖3 江陰大橋主梁斷面顫振導數

圖4 跨中節點豎向加速度時程

2 結構最不利響應的概率分布特征

風場的模擬過程存在隨機性,即由于規范譜的分解存在隨機性,平均風速相同的情況下,每次得到的風速時程總是不同的,使時程計算結果總是不同。當平均風速為40 m/s時,通過對10組不同的脈動風速時程計算結構跨中豎向位移的最大值可發現:各組中最大加速度均不相同,豎向加速度最大值為3.75 m/s2,最小值為2.19 m/s2,結構加速度響應的變化幅值為41.6%;橫向加速度最大值為0.20 m/s2,最小值為0.15 m/s2,結構加速度響應的變化幅值為26.1%。

為了研究不同風速時程下結構的響應規律,取結構最不利部位的加速度進行分析。取平均風速為10～60 m/s分組進行研究,每組取10次不同的脈動風模擬結果進行計算。現給出風速為40 m/s的結構響應曲線,如圖5所示,從上到下依次為10組不同脈動風對應的結構響應。

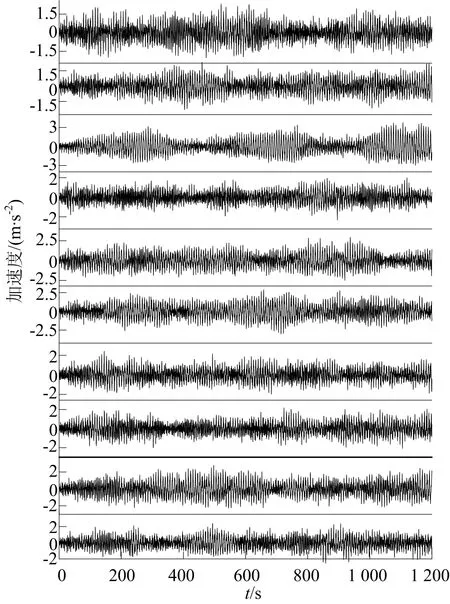
圖5 40 m/s風速時豎向加速度時程

通過計算不同風速下各組的加速度時程并對其統計與整理,可得到風速變化時結構加速的均值、標準差等統計參數,見表1所列。

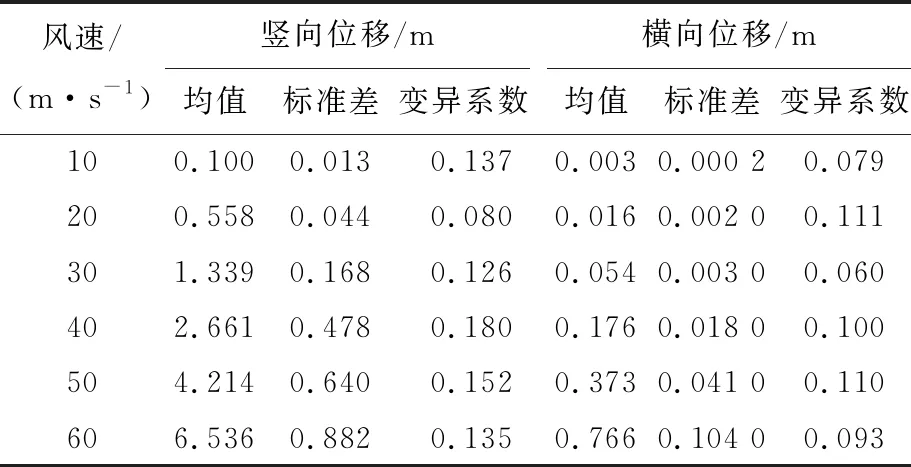
表1 不同風速跨中最大加速度統計表

對上述計算結果進行曲線的擬合,得到結構在不同風速下的最大加速度曲線,如圖6所示。

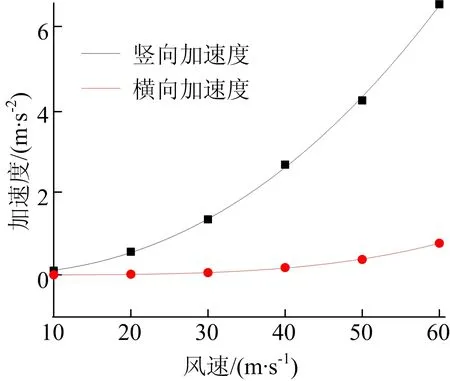
圖6 跨中最大加速度曲線

通過對計算結果進行擬合,可分別得到最不利情況下,豎向最大加速度曲線計算公式和橫向最大加速度曲線計算公式為:

Y=axb

(3)

對于豎向有:

a=6.052 26×10-4± 9.766 22×10-5,

b=2.267 12 ± 0.040 47;

對于橫向有:

a=1.471 93×10-7± 5.063 4×10-8,

b=3.776 23 ± 0.085 09。

對于得到的加速度曲線進行分析,結構跨中最不利部位的加速度最大值均值隨風速變化呈冪指數形式增加,即結構的顫抖振響應在惡劣風環境下的變化較良態風環境更加敏感;對于豎向和橫向加速度曲線進行分析,結構在豎向的加速度響應全風速下均大于橫向。隨著風速不斷增加,豎向加速度響應變化幅值也大于橫向的變化,故結構在豎向的結構響應較橫向更加敏感。運用該曲線可計算出任意風速下結構跨中加速度最大值的均值,為結構響應的概率性分析提供了依據。

同一風速下,確定結構最不利部位的最大響應符合何種分布是計算結構損傷概率的基礎。現階段對大跨橋梁最不利部位的最大響應分布并沒有統一意見。為研究結構不同風速下結構響應的概率分布,代表性地取其分布為正態分布。本文分別對30 m/s和40 m/s風速下10組結構的加速度響應峰值進行擬合,驗證其概率分布的類型，得到其概率分布Q-Q圖如圖7、圖8所示。

從圖7可以看出,當結構所受平均風速相同時,其豎向加速度和橫向加速度總是圍繞其標準線呈均勻分布,基本符合一條直線,可得到結構最不利部位的加速度最大值在豎向和橫向總是服從正態分布。

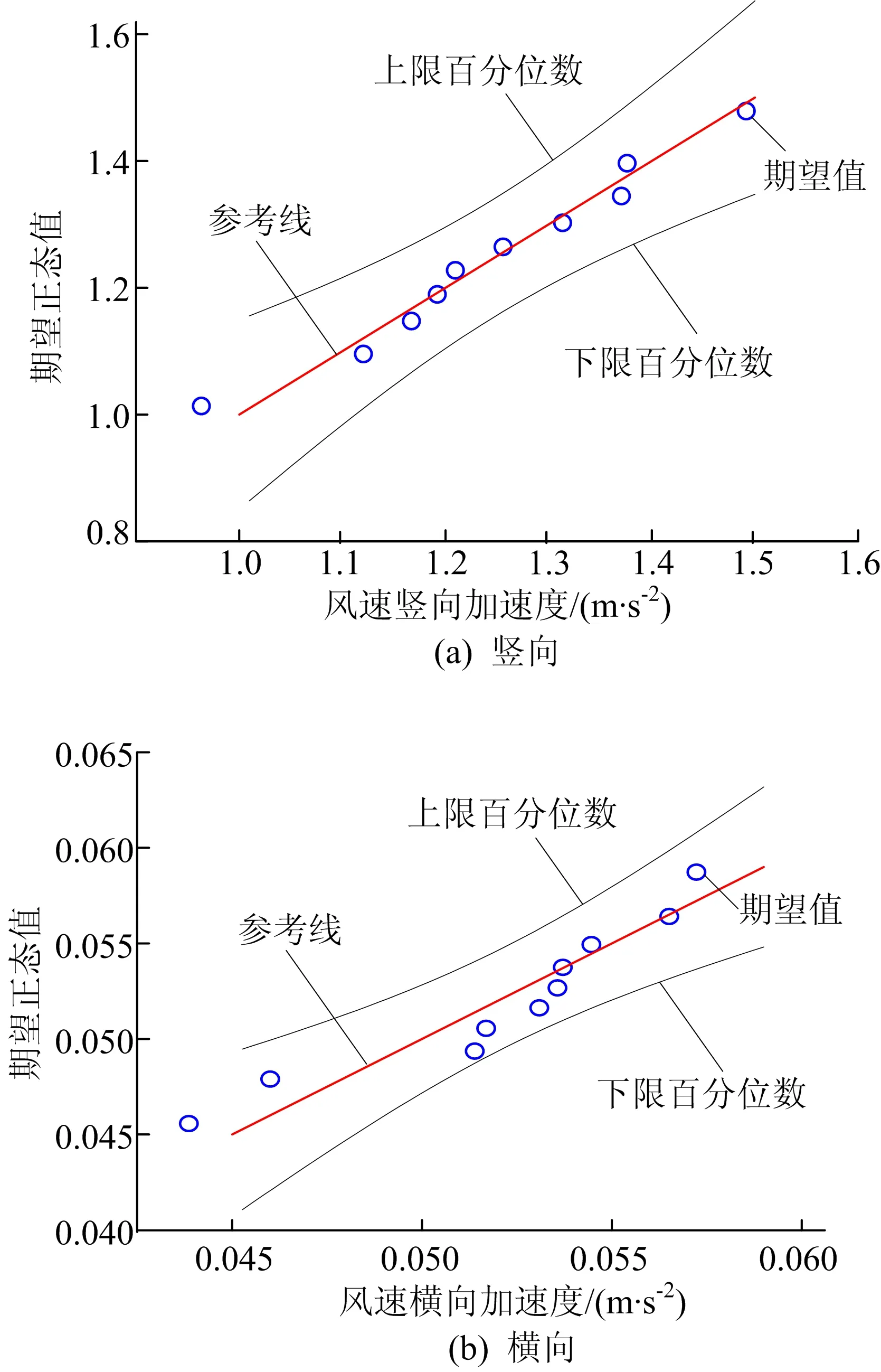
圖7 30 m/s風速下結構加速度響應Q-Q圖>

圖8 40 m/s風速下結構加速度響應Q-Q圖

通過對圖7、圖8結構加速度響應Q-Q圖分析,當結構所受平均風速不同時,相同方向下結構最不利部位的加速度最大值總是圍繞其標準線呈均勻分布,基本符合一條直線,即可認為結構最不利部位的加速度最大值總是服從正態分布且與結構所受平均風速的大小沒有關系。

綜合上述計算和驗證結果,可根據同一風速下結構的均值和方差擬合出該風速下結構響應的概率分布曲線,用于計算結構響應超越某界限的概率值,得到結構的損傷概率。現給出40 m/s風速下豎向加速度響應概率分布圖如圖9所示。

圖9 40 m/s風速豎向加速度響應概率分布

該曲線擬合時,取頻數分割間距為0.01。通過該概率分布圖,可計算出任意加速度界限下結構在該風速時的損傷概率。

對于其余風速未給出計算響應的均可通過圖7中擬合所得公式計算出結構加速度最大值的均值。通過給定變異系數的均值可求解結構加速度響應最大值的標準差。依據所得均值與標準差就可擬合出結構在該平均風速下的概率分布曲線。

3 橋梁顫抖振易損性曲線和概率評價

3.1 評價標準的界定

抖振是一種強迫振動,在各風速下均可能發生,但其往往不會引起結構毀滅性的破壞。國內外現階段對抖振響應的研究現階段多集中于荷載振動引起的疲勞和抖振對不同橋型產生的影響。橋梁作為交通樞紐,往往是一個國家或一個地區的交通命脈,有交通量大、交通組成復雜等特點。在破壞范圍內的振動,尤其是長距離的交通運輸往往會對行車和行人的舒適性產生影響。文獻[9]依據模擬試驗將行人舒適度分為“非常好”、“好”、“一般”、“差”、“無法忍受”5個等級;同時對于行車舒適度也給出了評價標準:豎向加速度aw峰值不大于3.6 m/s2,橫向加速度au峰值不大于2.4 m/s2。

對于行人舒適度的各級評價標準劃分見表2所列。

對大跨度橋梁影響概率P而言,其影響因素是復雜多變的,若將其影響因素產生的概率用數值的形式可表示為:

P=(a1,a2,a3,a4,…)

(4)

結構損傷的概率則可以表示為:

Pd=1-Pmax(a1,a2,a3,a4,…)

(5)

其中:Pd為結構的損傷概率;Pmax(a1,a2,a3,a4,…)為各種影響因素下結構在該等級評價標準上限的累計概率。

基于行人舒適度的評價標準,本文將結構損傷程度分為4個等級:等級1時豎向加速度aw>0.3、橫向加速度au>0.15;等級2時豎向加速度aw>0.85、橫向加速度au>0.4;等級3時豎向加速度aw>1.45、橫向加速度au>0.65;等級4時豎向加速度aw>2.0、橫向加速度au>0.9。

3.2 基于行人舒適度的損傷評價

任意影響因素對結構損傷的概率都是不同的,單一因素對結構產生的影響可通過上述評價標準,通過計算不同風速下的累積概率得到。對于行人舒適度而言,結構發生顫抖振時隨風速變化時的各級損傷曲線[14-16]如圖10所示。

對得到的基于行人舒適度評價標準的損傷曲線進行分析可知，隨著風速的不斷增加,結構在該等級下的損傷概率也不斷增加。依據文獻[11],江陰長江公路大橋設計風速為40.8 m/s。對于豎向損傷,損傷程度最高的四級損傷在風速為30 m/s2時其損傷概率仍然為0,風速在30～40 m/s2時其損傷概率增長迅速。對于橫向損傷,當結構處于良態風荷載作用下時,最低損傷程度的一級損傷在較高風速下損傷概率較高外,其余等級的損傷概率均為0。綜合對比圖10a和圖10b可知,相同損傷等級時風速增大,豎向損傷總是比橫向損傷對風環境更加敏感,即結構的損傷主要由豎向損傷控制。

綜合考慮上述2個方向的損傷曲線圖10a、圖10b可以看出,結構在良態風荷載產生的顫抖振作用下,行人舒適程度較差但處于可承受范圍內;結構在風荷載產生的顫抖振作用下,行人舒適度的損傷由豎向結構響應控制。

3.3 基于行車舒適度的損傷評價

對行車舒適度而言,基于加速度的評價標準較為簡略。可定義其對橋梁損傷程度標準為:豎向加速度峰值aw>3.6 m/s2,橫向加速度峰值au>2.4 m/s2。考慮行車舒適度時,結構發生顫抖振時隨風速變化的損傷曲線如圖11所示。

對得到的基于行車舒適度評價標準的損傷曲線進行分析可知,在良態風荷載產生的顫抖振作用下,豎向和橫向的損傷程度均較小,結構行車舒適度高。對比豎向損傷曲線和橫向損傷曲線可以發現,隨著風速的增加,豎向損傷對風荷載的作用更加敏感,橫向豎向損傷對風荷載產生作用的損傷較緩慢,則風荷載作用下,結構顫抖振對行車舒適度的損傷程度主要由豎向響應控制。

4 結 論

本文建立了基于性能的大跨度橋梁顫抖振性能概率性評價方法,得出了結構最不利部位響應的概率分布,基于行人舒適度與行車舒適度評價標準,對該結構的損傷程度進行了計算,得到結構在2種評價標準下的損傷曲線并對結構的損傷進行了概率評價。主要結論如下:

(1) 對不同風速下結構的多組最不利響應進行分析,擬合出了結構響應隨風速變化的響應曲線。通過該曲線可得到任意風速下結構最不利部位的最大響應均值隨風速大小呈冪指數增加。

(2) 通過對相同風速下多組計算結果分析,驗證了在考慮風場隨機性時,結構最不利地位的響應概率服從正態分布且與風速無關。

(3) 參考行人和行車對振動的評價標準,提出了基于舒適度的振動損傷評價標準。在此基礎上對顫抖振響應引起的振動對舒適性的損傷程度進行了評估。擬合出了隨風速變化時該標準下結構的損傷曲線。

(4) 考慮結構顫抖振響應的影響,對行人與行車舒適性進行了分析，良態風作用下,行人舒適度差,行車舒適性好。同時結構在豎向和橫向響應綜合考慮時,其豎向損傷對顫抖振響應更加敏感。