經歷探究過程 感悟數學思想

劉小艷

【摘要】本文結合小學數學教學實例，闡述通過探究倍量關系感悟數形的魅力，尋找等量關系感悟轉化的便捷，把脈內在關系感悟函數的神奇的策略，引導學生在探究過程中感悟數學思想，提高分析問題和解決問題的能力。

【關鍵詞】小學數學數學思想數學方法探究教學

【中圖分類號】G【文獻標識碼】A

【文章編號】0450-9889（2021）41-0118-02

引導學生開展數學知識的探究學習，讓學生在習得知識的同時，受到數學思想的熏陶，是當下小學數學教學改革的方向和趨勢。因此，在教學中，教師應智慧謀劃，轉變觀念，改進教學，不僅要關注教材的編寫、知識架構等要素，還應關注學生的知識水平、經驗積累和數學思維狀態等情況，科學創設有利于學生參與、思考、合作、分享、質疑、爭辯的學習情境，促使學生更積極、快樂地學習數學，讓數學教學朝著新課標所要求的方向和更適合學生的方向邁進。

一、探究倍量關系，感悟數形的魅力

數形結合的方法對于小學生研究較復雜的數學問題大有益處，很多時候能起到事半功倍的效果。如在解決倍量關系等較為復雜的問題時，教師就可以有機滲透數形結合的思想，一方面引導學生用直觀、形象的線段圖或長方形圖、圓圈圖等，表示數量以及數量之間的關系，讓學生在畫圖過程中較好地感知倍量關系，明晰數量之間的內在聯系；另一方面通過直觀圖指導學生探尋數量之間的內在聯系，從中探尋問題的突破點，使各種數量關系清晰化、明朗化。隨著問題研究的深入，學生的思維得以發展，數學活動經驗有所擴充和積累。

例如，四年級學生在學習中遇到以下問題：琳琳家有一籃子桔子，第一天吃了總個數的一半少3個，第二天吃了余下的一半少2個，第三天吃了6個，發現籃子里一個桔子也沒有了。問琳琳家原來一共有多少個桔子？

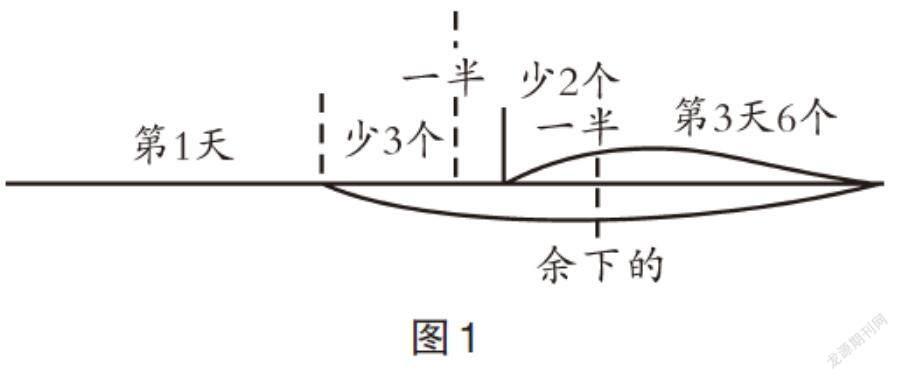
看到問題后，很多學生直呼“太難了”。的確，對于小學四年級學生而言，要解讀清楚如此復雜的數量關系，難度比較大。此時，教師要化繁為簡，引導學生用最直觀的線段圖來描繪習題中的各種數量關系（如圖1所示），于是，原本錯綜復雜的數量關系一下子就簡單明晰了。

很快，學生在畫圖的過程中便梳理好了題目中的數量關系：第3天6個（曲線部分），它超過余下一半2個，那么余下的一半就是6-2=4（個），發現余下的則是4+4=8（個），或4×2=8（個），這8個桔子不是總數的一半，它還包含超過總數一半3個，所以總數的一半是8-3=5（個），再算出總數就是5×2=10（個）。

教師通過畫線段圖的方式引導學生厘清習題中的數量關系，成為解決復雜倍量關系問題的關鍵所在。由此看來，小小的線段圖可謂蘊含著莫大的學問。這就需要教師巧妙地引導學生去分析倍量關系，并畫出對應的解題圖。借助解題圖學生能更精準地厘清數量關系，從而助推學習走向深入，并在解決問題的過程中感知數形結合方法的優勢，逐步提高分析問題的能力，從而有效提高數學素養。

二、尋找等量關系，感悟轉化的便捷

等量關系是小學數學中最常見的關系之一，它揭示了數量之間的相等關系，這也為學生更科學地分析數量關系、解決問題提供了有力的依據。為此，教師要靈活設計問題，有意識地引導學生去分析和思考問題，讓他們在厘清等量關系的過程中，跳出思維的局限，較好地解決問題，并逐漸受到數學轉化思想的熏陶，感知該方法的便捷優勢。

例如，在四年級“升和毫升”的練習課中，有這樣一道有趣的習題：李明明把800毫升的果汁，倒入2個大杯和4個小杯中，剛好倒滿，發現1個大杯的容量比2個小杯之和少40毫升，1個大杯的容量是多少毫升？1個小杯的容量是多少毫升？

在做這道題時，教師可以引導學生運用轉化策略，嘗試用轉化思想去分析問題，解讀其中的數量關系，進而實現思維能力的升級。分析這道習題，有“大杯”和“小杯”的不同論述，無形中增大了學生厘清問題的難度，對此，教師可引導學生重點分析大杯容量與小杯容量之間的關系，讓學生運用轉化思想，使問題變成學生學習過的、研究過的問題，以此助推學習的順利開展。具體方法如下。

首先，解讀文本。教師先指導學生閱讀習題，在閱讀中抓住關鍵句“1個大杯的容量比2個小杯之和少40毫升”，此時，教師可追問學生：“對于這句話，你是怎么理解的？”問題促使學生把注意力和思考的焦點都集中到這句話上。很快就有學生分享了自己的解讀思路：“1個大杯比2個小杯少40毫升，我認為可以把大杯變成小杯，也就是說，1個大杯變成2個小杯，不過不是正好相等的量，而是少40毫升。所以，2個大杯都換成小杯，就是2×2=4，4個小杯，還少40×2=80（毫升）。”該生的文本解讀為其他學生的學習思路開啟了一扇智慧之門。其他學生沿著這條思路繼續思考，并在演算中很快就明白了轉化的原理，整個學習活動也因此變得更加順暢和有活力。

其次，學習轉化。解讀文本是學習轉化的前奏，也是基礎和保障。在實際教學中，教師在學生閱讀習題、把握住關鍵句之后，還要引導學生進行有效的轉化。

師：剛才有同學對大小杯之間的關系進行了分析，你能沿著這條思路繼續思考嗎？

學生在回憶前面同學的分析后，再度閱讀習題中的關鍵句。

生1：把大杯都變成小杯，2個大杯就相當于4個小杯，還少80毫升。這樣一來，原來倒滿的2個大杯和4個小杯，就變成了8個小杯，但是還少80毫升。所以，我們可以補上80毫升，這樣就需要800+80=880（毫升）了，那么1小杯的容量就是880÷8=110（毫升）了，1個大杯的容量則是110×2-40=180（毫升）。

師：他的思考，你聽得明白嗎？可以嘗試用示意圖展開分析。

學生根據自己的思考和這位同學的分析畫出示意圖，再度進行探究，發現這位同學的分析是正確的，過程也是合理的。

生2：老師，其實我們還可以來驗算的。2個大杯、4個小杯一共是180×2+110×4=360+440=800（毫升），符合題目中的條件，說明我們的思考和計算都是正確的。

師：很好！自覺驗算是一種好習慣。你還有其他的思考嗎？

生2：當然，也可以把小杯變成大杯，根據“1個大杯比2個小杯少40毫升”這句話的意思，2個小杯相當于1個大杯，不過不是少40毫升，而是多出40毫升，這是最容易出錯的地方。所以4個小杯變成2個大杯，還多出40×2=80（毫升），最終是4個大杯多80毫升，也就是說果汁的總量是800毫升。計算過程如下：4÷2=2（個），這是大杯；2+2=4（個），這是大杯；40×2=80（毫升），800-80=720（毫升），720÷4=180（毫升），這是1個大杯的容量；（180+40）÷2=110（毫升），這是1個小杯的容量。我覺得這樣的思路和計算也是可行的，兩種方法的答案是一樣的。

……

師：經過對這個問題的研究，你有哪些收獲？

生3：把有關系的大小杯進行轉化，變成同一種杯子才能更好的計算。

師：是的！要抓住關鍵句去思考，并把其中一種杯子轉化為另一種杯子，這樣學習起來就簡單多了。

用轉化思想去分析、研究問題，在小學數學中比比皆是。要讓學生科學地去分析問題，正確地運用這一策略，需要教師給予學生必要的學習引導，讓他們在學習過程中自覺接受轉化思想的洗禮，了解轉化策略的原理，并學會使用該方法去解決問題。

上述案例，讓筆者還意識到，小學生對于轉化思想并非一無所知，他們只是還不能科學描述、規范使用而已。所以，在教學中教師要巧妙引導學生，激活學生這方面的感知能力，讓他們通過對具體問題的研究，進一步感悟轉化思想，掌握轉化策略，并積累學習經驗，形成和具備研究問題、解決問題的能力。

三、把脈內在關系，感悟函數的神奇

數學課程標準要求大力發展學生的“四基”（指數學的基礎知識、基本技能、基本思想、基本活動經驗），幫助學生積累更為豐富的數學活動經驗，努力提升學生的綜合素養。教師應正視這些要求，改變教學方式，努力做到以學生為本，營造適宜的教學氛圍，引領學生去探究、去合作。在小學數學教學中，教師要把滲透數學思想方法放在一個恰當的位置上去思考，以此助推學生素養的提升、能力的發展。

小學數學知識大多比較抽象，一些數學問題更是充滿玄奧，對于小學生而言，學習這些知識、研究這些問題非常吃力。對此，教師應相機滲透函數思想，讓學生在學習中得到相應的鍛煉。

例如，三年級學生在學習“長方形的周長與面積”之后，遇到下面這個問題：王大伯計劃用24根1米長的竹籬笆圍一塊長方形或正方形菜地。你打算如何幫助王大伯去設計菜地呢？

面對問題，有部分學生感覺無從下手。于是，教師適時滲透函數思想，引導學生有序分析。

生1：圍成正方形菜地的周長是24米，邊長就是24÷4=6（米），面積是6×6=36（平方米）。

師：那圍成長方形，該怎么辦呢？

生1：可以是長23米、寬1米，面積是23×1=23（平方米）。

生2：不對！長23米、寬1米的話，它的周長是（23+1）×2=48（米），而題目中的竹籬笆只有24米，所以錯了。

生2：圍成長方形，“長+寬”僅是周長的一半，也就是24÷2=12米。按照這樣的思路，那可以是：長11米、寬1米，面積是11平方米；長10米、寬2米，面積是20平方米；長9米、寬3米，面積是27平方米；長8米、寬4米，面積是32平方米；長7米、寬5米，面積是35平方米；還有剛才研究過的正方形，每條邊長6米，面積是36平方米。

生1：噢，我知道了！正方形的面積是最大的，而第一種的面積是最小的。

解決問題并不都是一帆風順的，需要學生進行必要的甑別與反思，并懂得靈活應用知識，還能交流經驗，學習才能慢慢向前推進。案例中，當學生有序地分析思考時，他們對周長一定，長與寬的變化規律就已經厘清楚了，并在計算過程中也想明白了。

同時，學生還發現：長越大，寬就會越小，此時的面積也是最小的；而隨著長變小，寬變大，面積反而逐漸增大，直至變成正方形，此時面積是最大的。如此反思甑別、感悟推想的過程，學生領略了函數思想的魅力。

由此可見，函數思想的運用能讓原本靜態的問題實現動態化，讓學生的學習思維動起來、轉起來，學習上也因此變得更加主動。當然，函數思想不只體現在這一層面，它在幾何初步知識的學習中應用尤為廣泛，還需要教師智慧引領，帶領學生去體驗。只有這樣，函數的相關概念才能在學生心中生根發芽、開花結果。

較之于數學基礎知識及常用數學方法，數學思想是處于更高層次的方法策略，在教學實踐中，教師應審時度勢，靈活滲透數形結合、轉化、函數等數學思想方法，以此助力數學問題的有效突破，增強學生自覺應用數學思想方法解決問題的策略意識。

【參考文獻】

［1］吳世彬，王善合.探索圖形規律 感悟數學思想——以西師大版四年級下冊“探索規律”為例［J］.小學數學教育，2014（9）.

［2］賴建軍.經歷探究過程 感悟數學思想——“植樹問題”教學片斷與思考［J］.小學數學教育，2015（23）.

（責編黃健清）