基于隱馬爾可夫模型的半掛車制動側滑狀態辨識
步玫,宇仁德,呂安濤,2,馬晨浩,胡婧暉
(1.山東理工大學 交通與車輛工程學院,山東 淄博 255049;2.山東省交通科學研究院,山東 濟南 250100)
目前,從我國的貨物中轉量來看,半掛車憑借它的較大貨運量完成了57.23%的貨物中轉,成為了公路運輸的主力[1]。同時,半掛車側滑事故也在日益增多,半掛車發生制動側滑后橫向先前移動,因其車身較長和自身質量大的特點,橫向滑行產生慣性造成的沖擊力較大,因此一旦發生事故往往較為嚴重。綜上所述,研究半掛車制動側滑的穩定性對道路交通安全具有重要意義。
在車輛狀態辨識方面,很多學者都進行了卓有成效的研究。史培龍等[2]首先采用PCA降維的方法對氣壓制動系統狀態進行辨識,然后運用駕駛人制動意圖與制動系統響應的雙層隱馬爾可夫模型對系統狀態進行識別,并分別依據實車試驗數據對模型進行離線訓練和在線辨識驗證;孟妮等[3]建立了基于RBF神經網絡的駕駛人無意識車道偏離識別模型,并通過歸一化、主成分分析和遺傳算法對神經網絡的權值和閾值參數進行優化,提高了神經網絡模型總體識別率;徐強[4]將CarSim仿真數據通過K均值聚類的方法對車輛行駛狀態數據進行離線聚類,得到4個離線聚類質心,搭建了CarSim與Simulink聯合仿真平臺,基于車輛實時行駛數據與離線聚類質心之間的歐氏距離設計了車輛橫向穩定性判定準則,對車輛行駛狀態進行實時劃分與識別;唐智慧等[5]應用Kohonen神經網絡對表征駕駛行為狀態的9個指標組成的向量進行非監督聚類,用聚類結果組成的時間序列表示駕駛員行為指標的動態變化特征并以此作為輸入,通過訓練SVM實現駕駛行為險態辨識,解決了高維指標數據監督聚類困難和險態識別的靜態性問題,并采用駕駛模擬器進行試驗設計,對方法的有效性進行驗證;游忍等[6]針對現有汽車防撞高速扇形模型提出了基于雙重擴展卡爾曼濾波的高速扇形預警模型,根據車輛狀態和路面附著系數估計實現了制動閉環控制;崔宇等[7]采用小波神經網絡對車輛運行狀態進行識別,對樣本進行主成分分析、卡爾曼濾波,利用遺傳算法優化小波神經網絡,優化后的小波神經網絡對數據進行訓練與測試,解決了車輛安全輔助系統中對車輛運行狀態識別率偏低的問題;劉通等[8]重點從車輛典型危險行駛狀態的識別、檢測2個方面,梳理縱向及橫向危險行駛狀態及其表征參數,總結主要的識別與檢測方法,得出了隱馬爾可夫模型對危險駕駛事件的識別準確率相對較高的結論。盡管上述方法在車輛狀態辨識上都有顯著效果,但由于車輛狀態的影響因素過多,從而也導致了模型中數據維度過高、訓練時間過長且辨識率偏低等缺點的存在。
本文選取重心橫向位置、重心縱向位置、制動初速度和路面摩擦系數4個重要影響因素作為模型的特征參數,在ADAMS中建立整車模型和道路模型進行直線制動仿真實驗,得到一系列特征參數仿真數據以及每條數據的仿真狀態,并選用Baum-Welch算法多次迭代得到HMM最優參數,以提高HMM模型的辨識準確率。
1 半掛車模型直線制動仿真實驗
1.1 基于ADAMS/CAR半掛車模型的構建
依據ADAMS/CAR中整車虛擬樣機的建模原則,本文所建的半掛車模型包括牽引車和半掛車兩大部分。牽引車為前橋轉向后雙橋驅動,轉向橋采用鋼板彈簧作為彈性元件,驅動橋采用空氣彈簧為彈性元件,由剛體車軸、減振器及橫、縱向拉桿等組成;半掛車由雙支撐、車身、輪胎等組成,采用空氣彈簧作為彈性元件[9]。將上述各子系統通過相應的通訊接口組裝成的半掛車仿真模型如圖1所示。
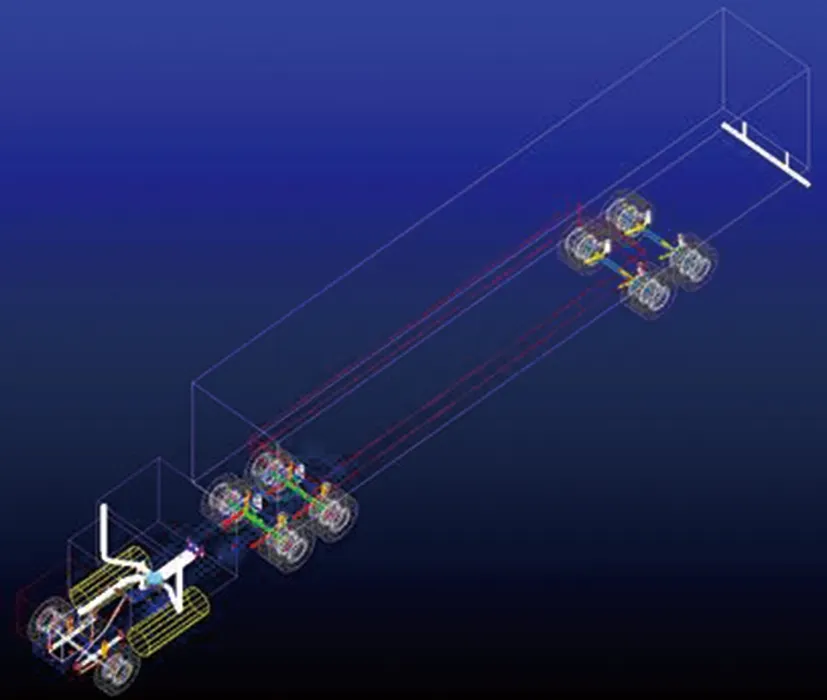
圖1 半掛車模型Fig.1 Semi-trailer model
1.2 道路模型的構建
在ADAMS/CAR標準模式下通過Road Builder建立一條直線形道路,保持其他參數不變,主要修改路面的摩擦系數即可,建好的3D道路仿真模型如圖2所示。

圖2 道路模型Fig.2 Road model
1.3 整車制動仿真
ADAMS/CAR通過在hps_frame_cg中改變質心坐標來調整重心位置,模擬車輛的重心偏移。實驗所構建半掛車模型的質心原點,也即重心初始位置(x,y,z)=(10 025 mm,100 mm,1 128 mm),且定義X軸,Y軸和Z軸方向的移動分別代表重心的縱向、橫向偏移和高度變化。在進行直線制動仿真實驗后,通過ADAMS/PostProcessor輸出的車速曲線圖,分別觀察重心在3個方向偏移時半掛車速度的變化情況可知,橫、縱向偏移對安全行車速度影響明顯,且分別在橫向偏移1dm和縱向偏移5 dm時更易觀察變化趨勢;因此,重心橫坐標在初始位置基礎上取值為100 mm、200 mm、300 mm、400 mm,同樣縱坐標取值為10 025 mm、10 525 mm、11 025 mm、11 525 mm。重心高度的變化對車速的影響不明顯,這跟半掛車自身重量較大有關,在這里只考慮重心的橫、縱向偏移。
修改道路屬性文件中的路面摩擦系數,分別取值0.8、0.7、0.6、0.5。最后在如圖3所示的對話框中輸入相應數據進行制動仿真實驗,設置制動減速度為0.4g,初始速度分別從低、中、高車速中隨機取值,其他參數保持不變。
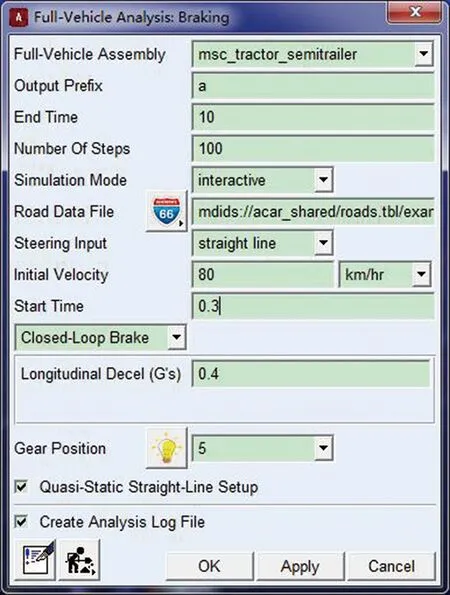
圖3 直線制動仿真參數輸入界面Fig.3 Straight brake simulation parameter input interface
仿真結束后,通過ADAMS/PostProcessor模塊分別輸出車身側滑角曲線圖和左右外側后輪所受側向力對比曲線圖,綜合兩個曲線圖判斷此次仿真是否已經發生側滑。當重心橫向位置為100 mm、縱向位置為11 025 mm、路面摩擦系數為0.8、制動初速度為84 km/h時輸出的兩種曲線圖如圖4和圖5所示。可以看出,半掛車在第4 s的時候車身側滑角遠遠大于0°,且左右兩輪所受側向力方向一致,說明在此速度下車輛已經發生了側滑。通過ADAMS輸出多組仿真數據以及每條數據的制動側滑狀態,根據仿真狀態將這些數據劃分為安全與危險兩組。

圖4 半掛車的車身側滑角Fig.4 Side slip angle of semi-trailer
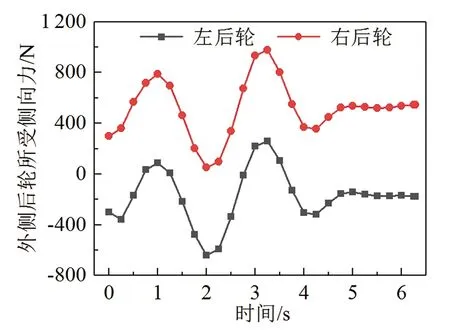
圖5 左右后輪受力對比圖Fig.5 Force diagram of left and right rear wheels
2 基于HMM的半掛車制動側滑狀態辨識模型的建立
本文主要研究利用重心橫向位置、重心縱向位置、路面摩擦系數、制動初速度這4個特征參數組,表征制動未發生側滑的安全狀態和已發生制動側滑的危險狀態。隱馬爾可夫模型可以定義為五元組λ={N,M,π,A,B},下面對各參數的意義進行說明。
車輛制動側滑狀態不能直接被觀察到,也就是HMM中所說的隱狀態,用參數N表示隱狀態數。本文的制動側滑狀態包括表征安全的狀態辨識1和表征危險的狀態辨識2,所以N=2。
制動側滑的安全與危險兩種狀態雖然不能直接通過觀察獲得,但是本文所選取的重心橫向位置、重心縱向位置、路面摩擦系數、制動初速度4個觀測信息均可以直接獲得;同時,這些觀測信息可以表征制動側滑的兩種隱狀態,也就是HMM中所說的觀察狀態,用參數M表示可觀察狀態的數目,所以M=4。
λ=(π,A,B)稱為隱馬爾可夫模型的三要素,π和A決定狀態序列,B決定觀測序列。狀態轉移概率矩陣A表示安全與危險兩個隱狀態之間相互轉移形成的概率矩陣;觀測概率矩陣B表示重心橫向位置、重心縱向位置、路面摩擦系數、制動初速度4個特征參數值之間相互轉移形成的概率矩陣;初始狀態概率向量π為制動側滑的兩個隱狀態所形成的初始概率矩陣。
3 HMM制動側滑狀態辨識算法及原理
3.1 Baum-Welch算法
Baum-Welch算法首先對HMM的參數進行初始估計,然后通過給定的數據評估這些參數的價值、減少它們所引起的錯誤并重新修訂這些參數;因此,對于給定的一組觀察序列,利用算法來估計一個最合適的HMM,也就是確定對已知序列描述最合適的λ=(π,A,B)三元組。
該算法本質上使用的就是EM(最大期望算法)的原理,即通過一種極大似然對數值(該值反映訓練出的模型與實際模型的接近程度,值越大越接近,也稱似然度[10])方法,不斷迭代訓練參數直到HMM模型收斂,最后得到最優參數。具體的參數學習過程如下:
1)參數初始化。隨機給πi,aij,bjk賦值,得到模型λ0,設i=0。
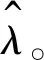
初始概率矩陣表達式為
(1)
轉移概率矩陣表達式為
(2)
觀測概率矩陣表達式為
(3)
式中:O和q分別為觀測序列和狀態序列。
4)保存模型參數。
3.2 辨識原理
本文采用的是一種離散的隱馬爾可夫模型(DHMM),首先分別對兩種隱狀態和4個特征參數進行分類編碼,見表1和表2(其中表2中車速的編碼原則是使每個區間內同時包含制動安全、危險兩種狀態);然后將所有的特征參數組作為觀測序列輸入到模型中進行機器學習和參數優化;最后利用建立好的HMM模型對十組具有代表性的特征參數值進行狀態辨識,其辨識原理如圖6所示。兩種辨識狀態分別對應兩個HMM辨識器,并且會產生兩個似然對數值Logi(P(O|λi))(i=1,2),即每種狀態都會有一個專屬的HMM,當輸入一組某狀態的特征參數數據時,此狀態對應的似然對數值就會最大。

表1 制動側滑狀態的分類編碼Tab.1 Classification and coding of braking sideslip
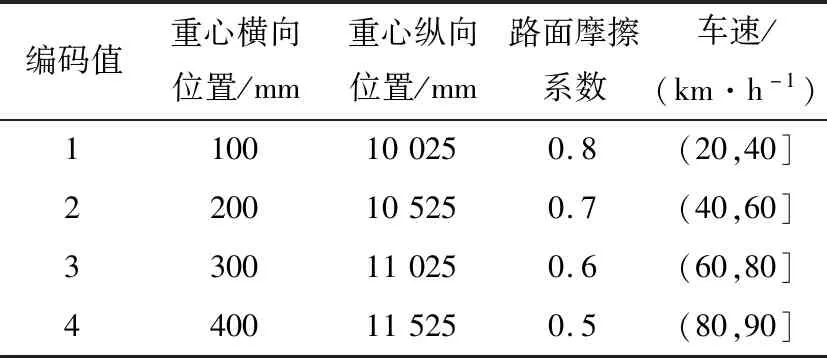
表2 特征參數的分類編碼Tab.2 Classification and coding of feature parameters

圖6 HMM的辨識原理圖Fig.6 HMM state recognition process diagram
4 HMM制動側滑狀態辨識模型驗證
4.1 參數輸出
通過MATLAB軟件對Baum-Welch算法進行編程,將包含安全與危險兩種狀態的仿真數據輸入到隱馬爾可夫辨識模型中進行參數迭代訓練,并通過似然度曲線變化圖可得迭代20次后安全狀態HMM1和危險狀態HMM2均達到收斂,如圖7所示。此時輸出優化后的兩模型參數πi,Ai,Bi(i=1,2),如下:
λ1=(π1,A1,B1),
λ2=(π2,A2,B2),
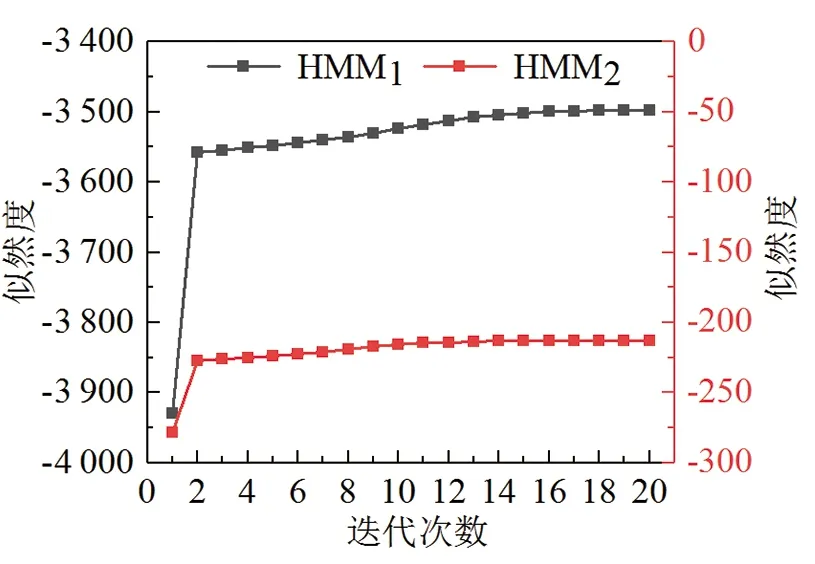
圖7 HMM的似然度曲線變化圖Fig.7 HMM learning curve with iterations
4.2 辨識結果
半掛車制動側滑狀態辨識結果見表3。分別選取5組安全和危險狀態下的特征參數樣本,并給出與這10組樣本數據相對應的制動側滑狀態HMM輸出的Logi(P(O|λi))。表3中顯示的這個似然對數值(負值)越大,說明某特征參數樣本與HMMi匹配程度越高,也即為該模型所對應的辨識狀態,表中用深色標注出正確的辨識結果,證明此辨識模型的有效性。
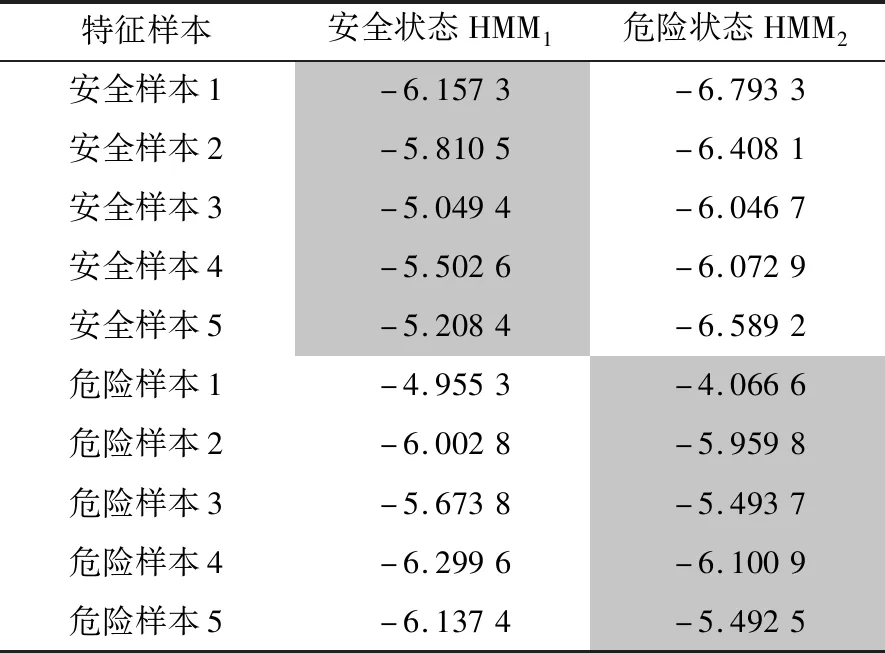
表3 半掛車制動側滑狀態辨識結果Tab.3 Identification results of brake slippage of a semi-trailer
4.3 準確性驗證
為了進一步驗證HMM制動側滑狀態辨識模型的準確性,將其與RBF神經網絡辨識算法[3]和BP神經網絡辨識算法[11]進行對比,隨機選取100組測試樣本分成10次進行辨識,記錄每一次得到的3種模型的準確率,對比結果如圖8所示。由圖8可知,本文所提出的HMM辨識模型優于其他兩種模型,且辨識準確率接近90%。

圖8 三種模型辨識準確率對比圖Fig.8 Comparison chart of three models′ recognition accuracy
5 結束語
車輛狀態辨識是主動監控預警技術的核心要素之一,本文通過ADAMS制動仿真實驗得到重心橫向位置、重心縱向位置、路面摩擦系數、制動初速度4個特征參數,構建了一種基于隱馬爾可夫模型的制動側滑狀態辨識模型,通過Baum-Welch算法實現了HMM模型的優化。辨識結果表明,優化后的模型能夠有效辨識半掛車的制動側滑狀態;準確性驗證表明,此模型具有辨識率高和魯棒性好等優點。

