基于Fast-ICA算法的改進EEMD算法在橋梁工程中的運用

羅燁鈳，陳永高，李升才

(1.浙江工業職業技術學院，浙江 紹興 312000；2.華僑大學 土木工程學院，福建 泉州 362000)

0 引言

橋梁在正常使用過程中，會受到外部荷載、有害物質以及自身材料老化等因素的影響，而發生不同程度的損傷[1]和抗力衰減。對于實際橋梁結構而言，當其結構自身發生一定的損傷時，其對應的模態參數會發生不同程度的變化；根據這一特性，有專家提出可通過監測橋梁結構自身模態參數[2]的變化情況來間接評估其整體狀態和損傷狀況。現階段，以振動分析為基礎的橋梁結構健康狀態[3]評估方法逐漸受到人們的重視，模態參數識別作為振動分析的關鍵問題之一，還需進一步完善。模態參數識別是指：對結構的振動信號進行動力特性參數的識別，以得到結構的頻率、振型以及阻尼比。實際橋梁結構中，為了精確地識別其模態參數值，首先應對結構自身的響應信號進行信號分解和重構，其次再對重構信號進行模態參數辨識。現階段，常用的信號分解算法是集合經驗模態分解算法(Ensemble Empirical Mode Decomposition, EEMD)[4]；常用的模態參數識別算法是隨機子空間算法(Stochastic Subspace Identification, SSI)[5]。隨著EEMD算法的普及，其缺陷也越來越明顯，其主要缺陷是分解所得本征模態函數(Intrinsic Mode Function, IMF)間存在模態混疊現象[6]和對于有效本征模態函數的定義沒有統一的標準。

鑒于此，本研究針對EEMD算法存在的不足提出將夾角余弦法用于篩選有效IMF分量，同時將盲源分離算法中的Fast-ICA算法[7]嵌入EEMD分解算法中以得到一種新的信號分解算法，并驗證該算法運用于模擬信號的可行性；將所提改進算法和EEMD算法分別運用于實測橋梁信號中，并采用隨機子空間算法識別重構信號以獲得模態參數值，對比所得模態結果與理論值以驗證識別結果的可靠性。

1 盲源分離算法的模型建立

盲源分離算法[8]的主要特點在于能夠依據輸出信號來估計推導出輸入信號和各組成信號，分離的過程屬于一種求逆的過程。以下介紹分離算法的主要步驟，以便將其與EEMD算法進行結合以實現系統信號的自適應分解。

建立盲源分離模型[9]的步驟：

(1)假設源信號為一組n維的信號矩陣，即X=[x1,x2,x3,…,xn]；

(2)假定混合矩陣為A，因結構系統處于環境條件下，即A為未知矩陣；

(3)源信號X=[x1,x2,x3,…,xn]在產生或傳輸過程中會與混合矩陣相作用，得到混合后的信號S=[s1,s2,s3,…,sn]，該S為傳感器在實際現場所測得的結構振動信號，屬于已知信號矩陣,表示如下：

S=X·A。

(1)

(4)對于式(1)，僅是知道混合信號S，還無法求解出源信號矩陣X，需要求解出混合矩陣A的逆矩陣A-，才能求解出源信號矩陣X；

(5)假定W=A-，則可得Y=W·S=W·X·A，其中Y為盲源分離算法的分離結果，可見，求解W是該算法的本質目的。

綜合上述步驟，可知盲源分離模型的建立流程圖如圖1所示。

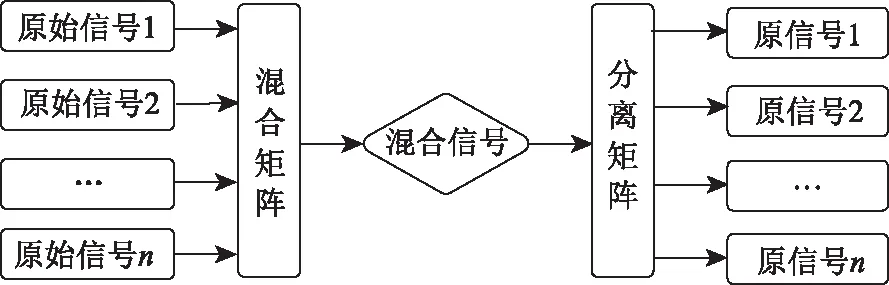
圖1 盲源分離模型流程圖Fig.1 Flowchart of blind source separation model

2 Fast-ICA算法

Fast-ICA算法由芬蘭赫爾辛基大學Hyv?rinen[10]等人提出，其基本原理是通過快速迭代比較來求解出最佳的分離矩陣。同時該算法為了保證各混合信號間不具相關性，對混合信號進行前期處理，即對混合信號進行中心化處理和白化處理，進而保證分離結果的準確性。

Fast-ICA算法主要分為信號的前期處理和算法迭代；以下分析這兩大步驟的具體流程。

2.1 前期處理-中心化處理

數據中心化處理能夠保證各樣本的均值為0，且不會改變樣本中數據點間的相互位置，同時也不會改變變量間的相關性。對數據進行中心化處理的主要目的在于使得采集到的混合矩陣各分量成為零均值向量，簡化算法步驟。

數據的中心化處理[11]是指平移變換，公式為：

(2)

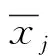
2.2 前期處理-白化處理

白化處理的主要目的在于保證混合信號S=[s1,s2,s3,…,sn]中各分量之間不具相關性，得到白化后的混合信號，簡化Fast-ICA算法的過程。其原理是將S=[s1,s2,s3,…,sn]或者噪聲的協方差矩陣進行對角化處理。

進行白化處理時，需滿足如下約束條件：

(1)獨立成分之間不具相關性；

(2)獨立成分不滿足高斯分布；

(3)混合矩陣需為方陣，若不滿足則需對S=[s1,s2,s3,…,sn]做白化處理，以便降低其組成的矩陣維數。

對S=[s1,s2,s3,…,sn]進行白化處理得到新矩陣Snew：

Snew=U·S，

(3)

式中，U為白化矩陣，Snew中各分量具有二階不相關性，且具有單位方差。對S=[s1,s2,s3,…,sn]的協方差進行特征值分解，可求得白化矩陣U。

U=VD-1/2VT，

(4)

式中，V為分解變量：求解S=[s1,s2,s3,…,sn]的協方差矩陣E[SST]的特征向量，組成正交矩陣以獲得分解變量V；D為對角陣，由各個特征向量所對應的特征值組成。

由式(3)和式(4)可得經白化處后的信號：

Snew=U·S=VD-1/2VT·S。

(5)

2.3 算法迭代

Fast_ICA算法是在獨立成分分析(Independent Component Analysis，ICA)算法[12]的基礎上改進所得，實質上屬于一種快速定點ICA算法，它在多次迭代對比中能找到一個單位矢量，使得wTs達到最大值。

定點算法迭代公式為：

wi(k+1)=E[sig(wi(k)T)si]-

E[g(wi(k)T)si]wi(k)，

(6)

式中g為一個非線性函數。

具體迭代步驟如下：

Step 1：假定i=1。

Step 2：隨機選擇范數為1的初始矢量w(0)，并假定k=1。

Step 3：采用式(6)。

Step 4：假定wi(k)=wi(k)‖wi(k)‖。

(7)

每對wi(k)完成一次迭代，則需對其進行一次歸一化處理[13]。歸一化處理的理由在于：Fast-ICA算法對信號的能量要求較高，所以必須通過歸一化處理來保證信號具有足夠的能量來完成算法。

Step 5：|wi(k)Twi(k-1)|收斂于1，則整個算法結束運算，并輸出矢量wi(k)；否則令k=k+1，返回執行(3)然后繼續迭代。

Step 6：若迭代后i的值等于源信號個數，則返回執行(2)。直至把所有的源信號分離出來。

基于上述步驟，便能通過循環迭代估算出各個獨立分量。為避免同一個獨立分量被反復迭代，這里需要在Step 4中加入一個正交投影，轉換為公式：

(8)

Fast_ICA算法的流程圖如圖2所示。

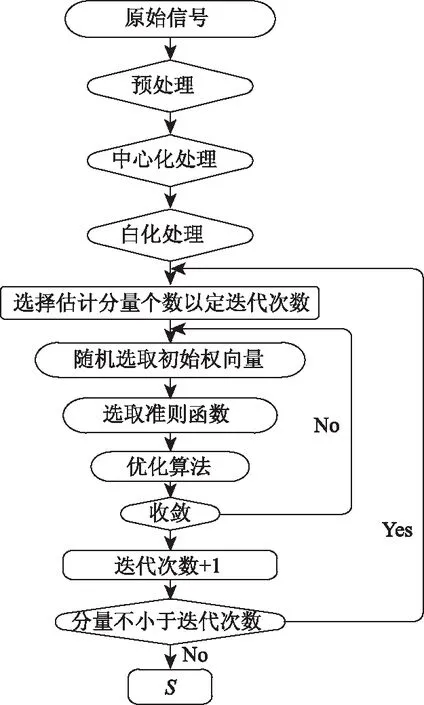
圖2 Fast-ICA算法流程圖Fig.2 Flowchart of Fast-ICA algorithm

3 EEMD算法的改進

EEMD算法是以EMD算法[14]為基礎改進而得，其原理為：將等幅值的隨機白噪聲添加到原始信號中，以改變信號內部極點的分布情況，使得各極點的分布更加均勻，進而避免高頻分量影響最終的分解結果；同時基于對所有結果取均值的方式來消除本征模態函數分量中的白噪聲。

隨著該算法的廣泛運用，不少學者[15]發現所得IMF分量間會發生模態混疊現象，即所得各IMF分量間會存在信息的重疊。鑒于此，本研究先將盲源分離算法中的Fast-ICA算法融入到EEMD算法中以避免模態混疊現象的發生。

3.1 EEMD算法的實現步驟

Step1：將N個不同的Gaussian白噪聲wi(t)(i=1,2,…,N)加入原始信號x(t)中得到xi(t)，即：

xi(t)=x(t)+wi(t)，

i=1, 2,…,N。

(9)

Step2：對xi(t)進行EMD分解得到IMFij和殘余項rij，j代表每次EMD分解后IMF的個數，即：

j=1, 2,…,n。

Step3：對所有IMF取平均，求得最終的IMF，即：

(11)

3.2 IMF分量的有效篩選

根據3.1節EEMD算法流程可知，對原始信號進行EEMD分解可得到一系列IMF分量。就如何辨識所得IMF分量是否為有效分量，沒有統一的處理方式；基于此，本研究引入夾角余弦法[16]對IMF分量進行篩選，具體實現過程如下：

Step1：考慮到各IMFj(j=1,2,…,n)分量和原始信號x(t)間的數據可能存在量綱差異，所以需要分別對其進行數據歸一化處理，以保證各組數據間具有可比性，計算公式如下：

(12)

式中，IMFj,min和IMFj,max分別代表IMFj的最小值和最大值；x(t)min和x(t)max分別代表x(t)的最小值和最大值。

(13)

3.3 Fast_ ICA算法的應用

基于3.1節和3.2節，可實現對原始信號x(t)信號分解，并獲得有效IMF分量。基于此，可通過如下算法流程將Fast_ICA算法融入到EEMD算法中以避免IMF分量間信息發生重疊現象。

Step1：基于2.1節所提算法，對有效IMFi(i=1,2,…,m)進行中心化處理，其中m為有效IMF分量的個數；

Step2：基于2.2節所提算法，對step1所得IMFi(i=1,2,…,m)進行白化處理；

Step3：基于2.3節所提算法，對step2所得IMFi(i=1,2,…,m)進行算法迭代，求解出最終的有效IMF；

Step4：利用式(14)對篩選出的有效IMF分量進行疊加以得到重構的有效信號X(t)；

(14)

基于夾角余弦法和Fast_ICA算法的改進EEMD算法流程圖如下：

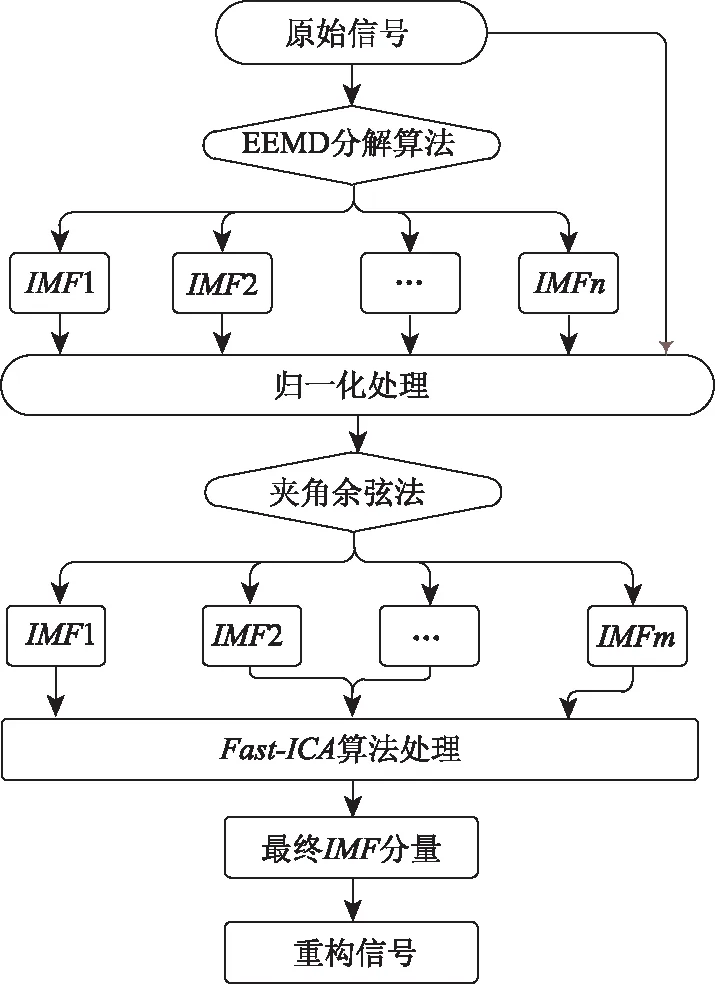
圖3 改進EEMD算法Fig.3 Improved EEMD algorithm

4 仿真信號驗證

仿真信號由1 Hz和0.1 Hz的正弦信號疊加0.5 Hz 的余弦信號，并疊加噪聲水平約為10%的隨機噪聲組成：

s(t)=1.5sin(2πt+π/8)+cos(πt+π/4)+

0.5sin(0.2πt+π/5)+10rand。

疊加信號共20 s，采樣頻率為100 Hz，即2 000個測試點，疊加信號時程曲線圖如圖4所示。

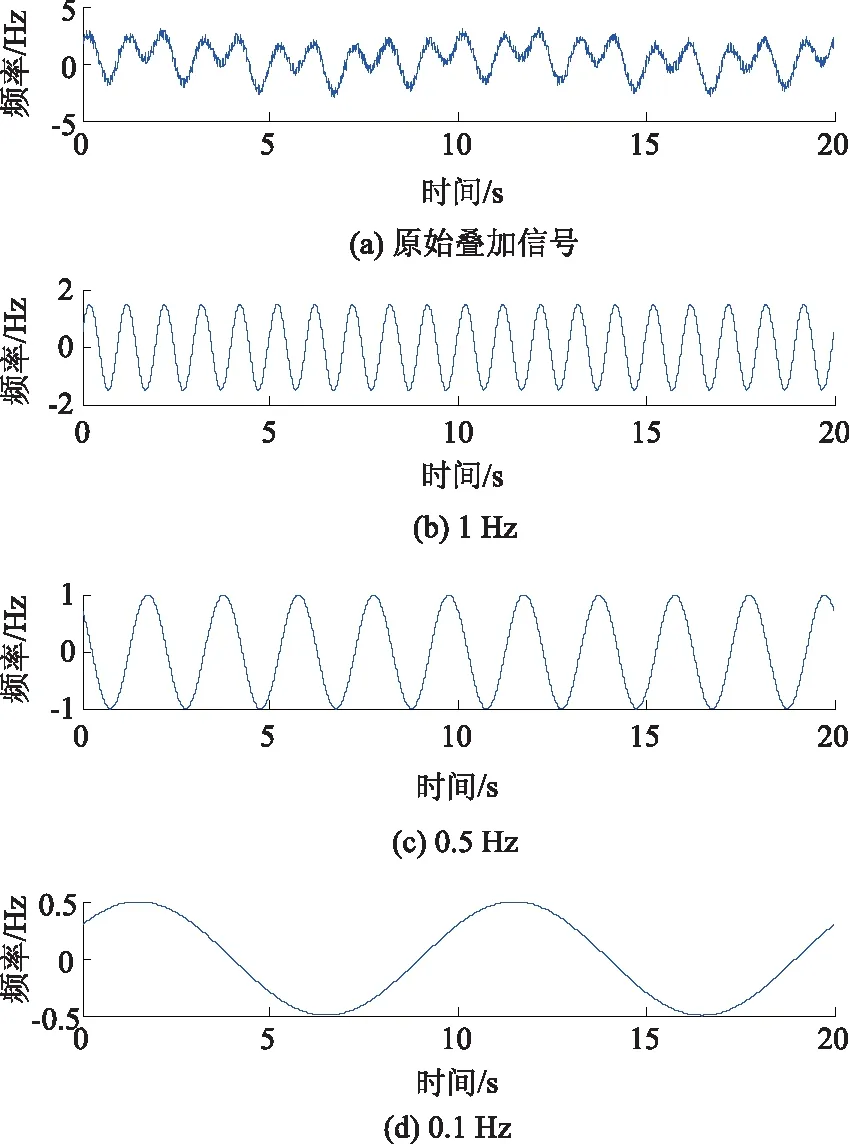
圖4 混合信號與疊加信號Fig.4 Mixed signal and superposed signal

4.1 EEMD分解結果

對疊加信號s(t)進行EEMD分解，分解結果見圖5，圖中第1行為原始信號的時程曲線圖，共分解得到10個IMF分量。

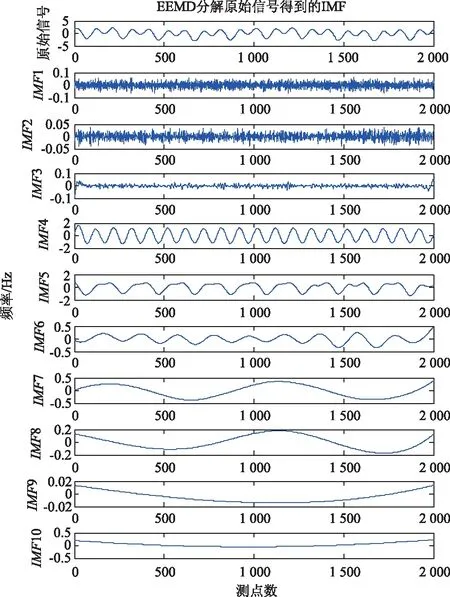
圖5 EEMD分解結果Fig.5 Decomposition result by EEMD algorithm

4.2 有效IMF分量

基于3.2節所提算法對上述10個IMF分量進行辨識，得到表1的關聯度系數。由表1中數據可知，只有IMF4，IMF5，IMF6對應的關聯度數值大于0.3，則將這3列IMF分量定義為有效IMF分量。

將所得有效IMF分量與混合信號中的各組成信號作對比，結果如圖6所示。其中有效IMF4分量與1Hz正弦信號的關聯度系數為0.89；有效IMF5分量與0.5Hz余弦信號的關聯度系數為0.83；有效IMF5分量與0.1Hz正弦信號的關聯度系數為0.63。

表1 各IMF分量與疊加信號間的關聯度Tab.1 Correlation between IMF component and superposed signal

4.3 改進EEMD分解結果

基于3.3節所提算法，對上述所得IMF4，IMF5，IMF63個有效分量進行Fast-ICA算法處理，并將所得結果與原始信號中的各疊加信號做對比，結果如圖7所示。其中有效IMF4分量對應的盲源分離結果與1 Hz正弦信號的關聯度系數為0.98；有效IMF5分量對應的盲源分離結果與0.5 Hz余弦信號的關聯度系數為0.97；有效IMF5分量對應的盲源分離結果與0.1Hz正弦信號的關聯度系數為0.93。

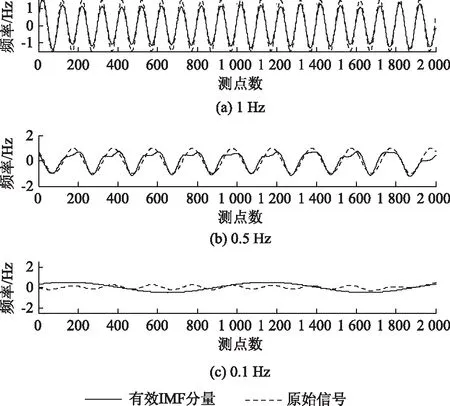
圖6 有效IMF分量與各信號的對比Fig.6 Comparison of effectiveness IMF component with signal

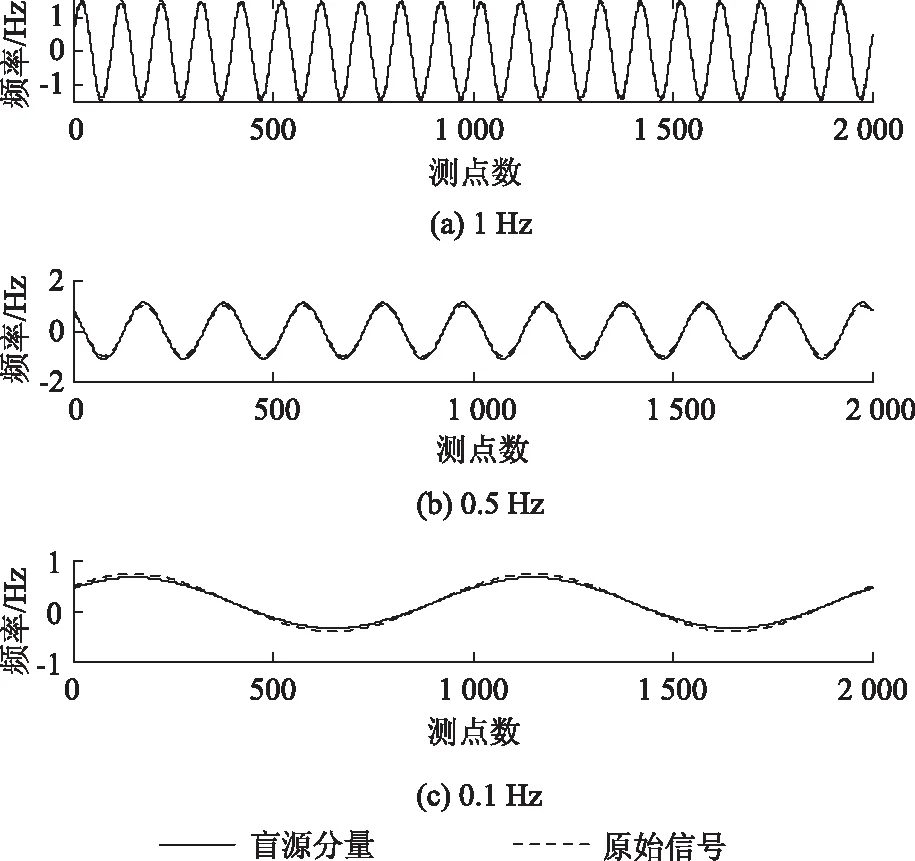
圖7 有效IMF分量對應盲源分離結果與各信號的對比Fig.7 Comparison of blind source separation result corresponding to effective IMF component with signal

4.4 重構信號

為進一步驗證改進EEMD算法所得重構信號更接近真實值，現將兩種算法所得重構信號作對比分析，結果如圖8所示。由圖8可知，本研究所提算法得到的重構信號與原始信號更接近，表明改進EEMD算法能夠提高既有EEMD算法的分解效率。

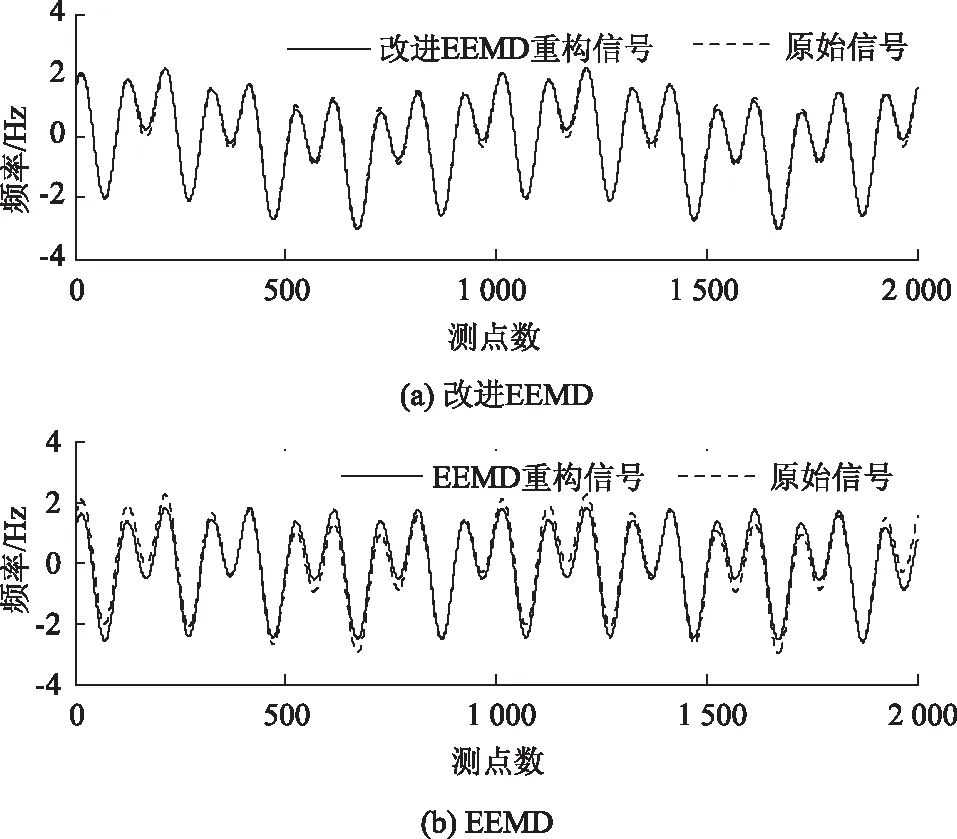
圖8 重構信號對比Fig.8 Comparison of reconstructed signals

5 不同噪聲水平的信號驗證

5.1 各疊加信號

為驗證所提算法能夠適用于不同噪聲水平的信號，在疊加信號s(t)的基礎上調整噪聲水平，得到新的疊加信號s1(t)和s2(t)：

s1(t)=1.5sin(2πt+π/8)+cos(πt+π/4)+

0.5sin(0.2πt+π/5)+5rand，

s2(t)=1.5sin(2πt+π/8)+cos(πt+π/4)+

0.5sin(0.2πt+π/5)+15rand。

兩疊加信號在0～20 s時間段的時程曲線圖如圖9所示。

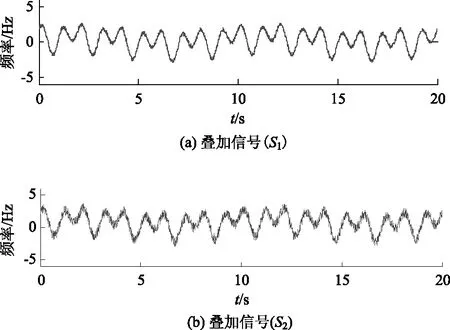
圖9 疊加信號Fig.9 Superposed signal

5.2 分解結果

基于第4節的分解流程，分別采用EEMD算法和改進EEMD算法對疊加信號s1(t)和s2(t)進行分解和重構。兩種分解算法所得重構信號如圖10所示，其中EEMD算法重構所得信號與原始信號間的關聯度系數分別為0.83和0.85；改進EEMD算法重構所得信號與原始信號間的關聯度系數分別為0.95和0.94。這表明改進EEMD算法適用于不同噪聲水平的信號，且分解的效率較既有EEMD算法更高。

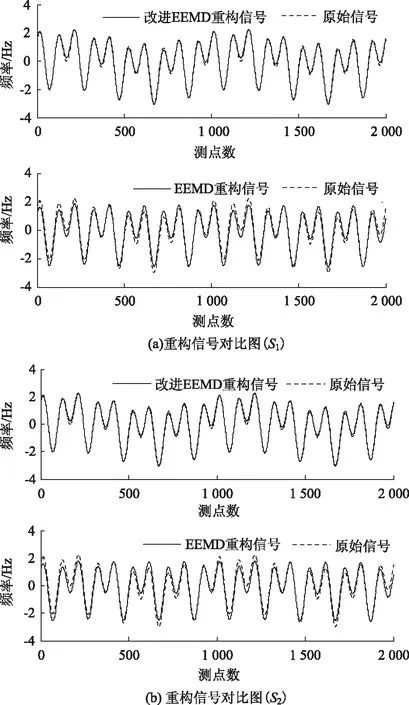
圖10 重構信號對比Fig.10 Comparison of reconstructed signals

6 簡支梁橋仿真算例

以某簡支梁為研究對象，以驗證所提算法適用于分解和重構橋梁結構的響應信號。

6.1 簡支梁橋

該簡支梁的長度為30 m，等分為10段，采用MIDAS軟件建立該簡支梁模型。其截面為箱型截面。為模擬環境激勵，將在節點2～10上分別豎直方向的白噪聲激勵，如圖11所示。

圖11 簡支梁橋Fig.11 Simply supported girder bridge

6.2 白噪聲的添加

白噪聲指功率譜密度在整個頻域內均勻分布的噪聲，添加白噪聲激勵的步驟如下：

(1)白噪聲的生成：基于MATLAB軟件中的randn函數命令生成一組均值為0，方差為1的9組隨機序列數據；圖12為其中一組白噪聲激勵的時程曲線圖。

(2)白噪聲的添加：基于MIDAS軟件平臺，在節點2～10上分別施加一組由Step1所得的隨機序列數據，以模擬環境激勵；

(3)在MIDAS軟件中做時程分析；

(4)提取該簡支梁在1 min內各節點的加速度響應信號，因采樣頻率為100 Hz，即可得到共6 000個測點數據。

圖12 白噪聲激勵Fig.12 White noise excitation

6.3 各節點的動力響應信號

因篇幅有限，僅給出節點4、節點6及節點8在采樣時間段內的加速度響應時程曲線圖，見圖13所示。

圖13 節點加速度響應Fig.13 Acceleration response of node

6.4 模態參數識別結果

分別采用EEMD算法和改進EEMD算法對11個節點的加速度響應信號進行信號的分解和重構，其次再采用隨機子空間算法[17-18]識別兩種分解算法所得重構信號，得到各自對應的穩定圖[19]，見圖14。表2給出了兩種算法對應的頻率值結果與MIDAS時程結果的對比表。

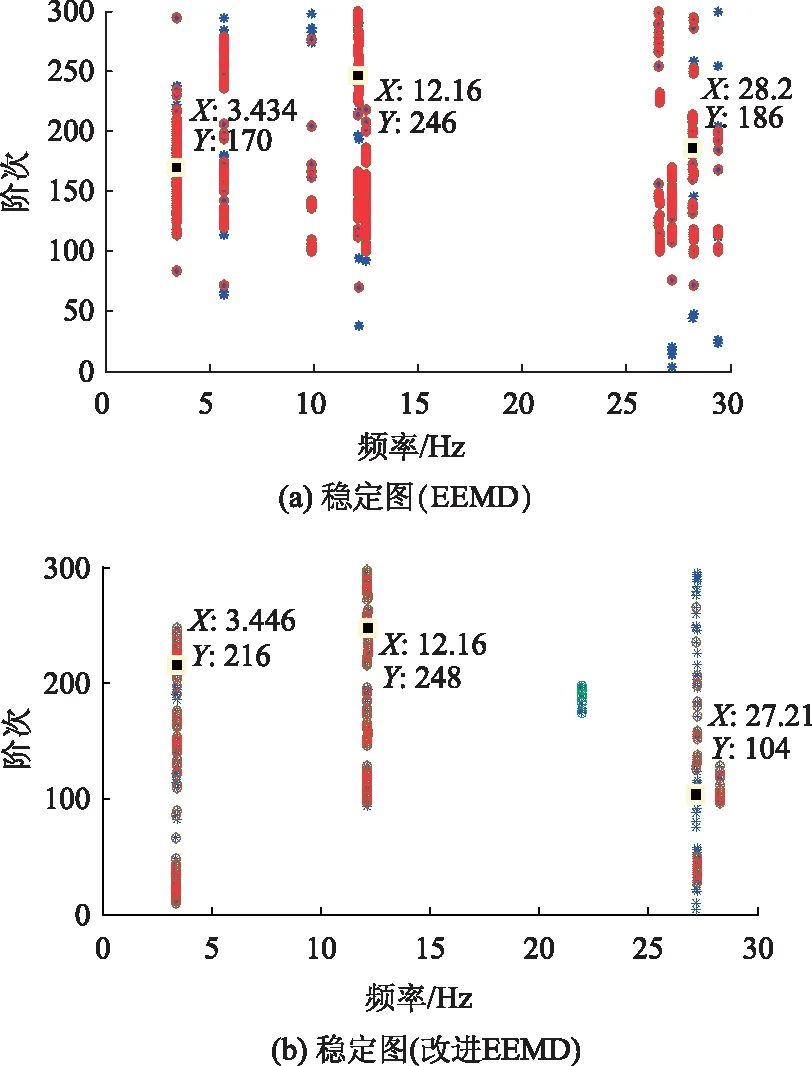
圖14 穩定圖Fig.14 Stabilization diagrams

根據圖14和表2可知：基于改進EEMD算法得到的穩定圖中頻率軸更為清晰；且基本不存在虛假模態，表明改進EEMD分解算法能夠有效地剔除環境激勵信號中的無用信息，更為真實地保留橋梁結構自身的結構信息。

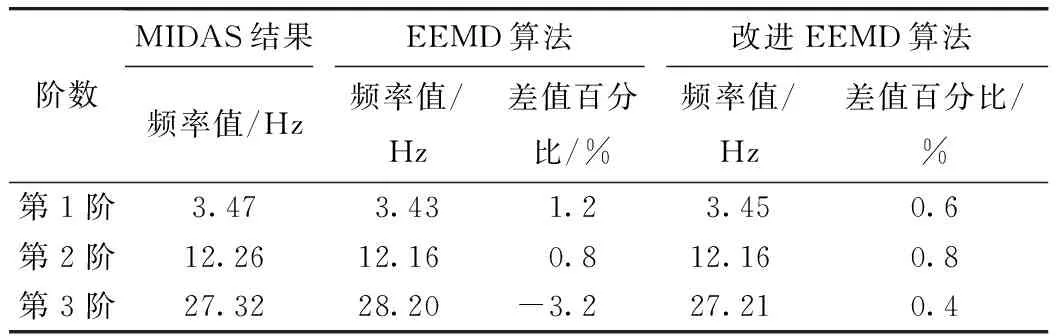
表2 頻率結果(單位：Hz)Tab.2 Result of frequency (unit:Hz)

為驗證改進EEMD算法能夠識別該簡支梁結構的模態振型圖，得到了其前3階模態振型圖。圖15為所得模態振型圖與理論振型結果的對比圖，其中橫坐標為節點編號，縱坐標為經標準化處理后的結構變形結果。可知識別所得前3階模態振型圖均與理論振型圖具有很高的相似度。

圖15 模態振型識別結果對比Fig.15 Comparison of modal identification results

7 實際橋梁信號驗證

以某斜拉橋的實測主梁振動響應信號為研究對象，首先對信號進行分解和重構，其次基于隨機子空間算法獲得對應的穩定圖；最后通過對比所得模態參數結果來辨別兩種算法的優劣。

該斜拉橋橋長共628 m，其中主跨為330 m，兩邊跨均為149 m，橋面凈寬18 m。其結構體系為雙塔扇形雙索面的塔梁分離懸浮體系，橋上總共布置11組加速度傳感器，主梁上的圓圈為傳感器大體布置位置。傳感器的信號采樣頻率為20 Hz，圖16為某傳感器采集到的時長為200 s的主梁加速度響應時程曲線圖。

圖16 加速度響應信號時程曲線Fig.16 Acceleration response signal time-history curve

7.1 真實模態參數結果

對于橋梁結構而言，模態參數結果主要為頻率、阻尼比和模態振型。現階段，由于對阻尼比的認知還不夠深入，識別得到的阻尼比結果存在空間和時間的變異性。因此，本研究僅分析該橋梁結構的固有頻率和模態振型。

為了獲得該斜拉橋的真實固有頻率值，已有相關檢測單位通過在主梁的主跨跨中采用跳車激振的方式對其產生一定的激勵，并基于傳感器收集的主梁振動脈沖信號進行分析識別得到了其自振頻率。圖17為該斜拉橋的前3階模態振型結果。

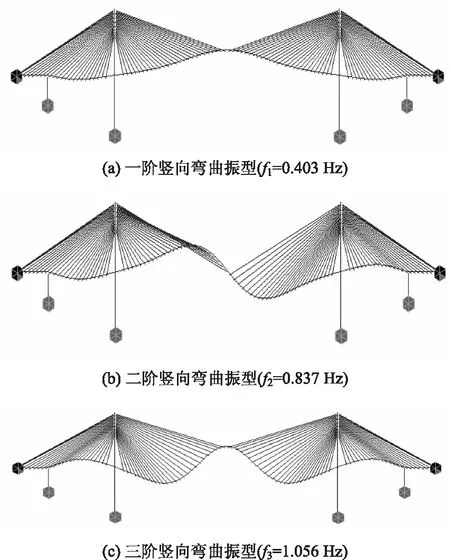
圖17 前3階模態振型(MIDAS)Fig.17 The first 3-order modal shapes(MIDAS)

7.2 穩定圖結果分析

采用隨機子空間算法識別兩種分解算法所得重構信號，得到各自對應的穩定圖，結果如圖18所示。對比兩圖可知：基于改進EEMD算法得到的穩定圖中頻率軸更為清晰；且基本不存在虛假模態，表明改進EEMD分解算法能夠有效地剔除環境激勵信號中的無用信息，更為真實地保留橋梁結構自身的結構信息。

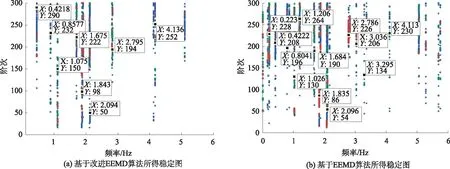
圖18 穩定圖結果Fig.18 Result of stability diagrams

7.3 頻率值結果分析

為了分析改進EEMD算法所得的穩定圖能夠獲得更為精確的頻率值，將兩種分解算法所得的前6階頻率值分別與跳車自振結果和MIDAS結果作對比，結果如表3所示。根據表中數據可知:

(1)基于改進EEMD算法所得穩定圖中獲得的前6階頻率值，其與跳車自振頻率值間的差值百分比范圍為[-0.9%,1.3%]；與MIDAS頻率值結果間的差值百分比范圍為[-4.7%,-1.8%]；

表3 頻率值結果對比Tab.3 Comparison of frequencies

(2)基于EEMD算法所得穩定圖中獲得的前6階頻率值，其與跳車自振頻率值間的差值百分比范圍為[-1.1%,6.6%]；與MIDAS頻率值結果間的差值百分比范圍為[-4.8%,3.9%]；

綜合上述可知：基于改進EEMD算法和隨機子空間算法所得穩定圖中頻率軸更清晰，且頻率值更接近理論值，表明該分解算法較現有的EEMD算法能夠更有效地剔除虛假信息，保留實際橋梁結構的真實信息。

7.4 模態振型結果分析

圖19為橋梁結構前3階模態振型圖，圖中橫坐標為傳感器布置位置，縱坐標為0-1化結構變形結果。通過對比圖19與圖17的MIDAS振型圖可知：識別所得前3階模態振型圖均與理論振型圖具有較高的相似度。

圖19 前3階模態振型Fig.19 The first 3-order modal shapes

8 結論

(1)可以利用“夾角余弦法”來實現有效IMF分量的辨識，且篩選的結果具有可靠性；

(2)將Fast-ICA算法融入到EEMD算法中能夠有效避免IMF分量間發生模態混疊現象；

(3)將改進EEMD算法和既有EEMD算法運用于仿真模擬信號中，具有更好的信號分解效率；

(4)將改進EEMD算法和既有EEMD算法運用于實際橋梁工程的信號分解中，并通過對比分析基于隨機子空間算法所得的模態參數結果可知，改進算法所得穩定圖具有更清晰的穩定軸，頻率值和模態振型均具有可靠性。