高原山區乘用車行駛工況構建方法研究

徐 婷，崔世超，劉 明，賀玉龍，石 鋒

(1. 長安大學 運輸工程學院，陜西 西安 710064；2. 長安大學 汽車學院，陜西 西安 710064；3. 北京工業大學 城市交通學院，北京 100124; 4. 中國汽車工程研究院股份有限公司，重慶 401122)

0 引言

汽車行駛工況是描述特定交通環境下車輛行駛特征的速度-時間曲線[1]，它能夠代表被測區域內車速變化規律[2]，對汽車節能減排有重大意義。中國國家標準化管理委員會于2019年10月下旬發布了中國標準行駛循環工況(CATC)，包括乘用車、輕型商用車、重型商用車的8條整車測試工況曲線及發動機工況曲線。此外，很多學者致力于汽車行駛工況研究:王楠楠[3]通過短行程法，采用模糊C均值聚類方法構建了合肥市的行駛工況。張宏等[4]通過短行程法，對不同車速區間賦予權重構建了呼和浩特市典型汽車行駛工況。姜平等[5]通過馬爾可夫鏈方法，利用最大似然估計分類方法構建了合肥市的行駛工況。劉應吉等[6]提出用組合主成分分析進行汽車行駛工況的構建。李耀華等[7]通過馬爾可夫蒙特卡洛方法構建了西安市城市公交行駛工況。國外[8-11]主要針對城市道路進行工況構建。查閱文獻發現，目前的工況曲線無法涵蓋高海拔地區。

高海拔地區生態薄弱，且隨著海拔升高，汽車動力性能下降，汽車排放引起的環境問題尤為嚴重，多山的地形條件讓汽車行駛工況與城市工況有很大差異。

本文以高原山區車輛的車況為研究對象，基于青藏高原川藏線(得達鄉—海子山段)試驗道路采集數據，根據汽車運行特點，提出了改進的短行程法，進行高原山區汽車行駛工況的構建。

1 數據采集及預處理

1.1 數據采集

通過對我國高原地區道路線形復雜程度、地理環境特點對比，選取青藏高原G318川藏公路南段(得達鄉—海子山段)道路為試驗道路。試驗路段最低海拔3 610.4 m，最高海拔4 591.6 m。

本次試驗選用多次參加道路試驗的3名駕駛員，試驗車輛為乘用車，車輛外廓尺寸等參數均在典型乘用車設計范圍內，具有代表性，車輛狀況良好。通過自主行駛法駕駛試驗車輛在試驗道路上行駛。車輛信息如表1所示：

表1 試驗車輛技術參數Tab.1 Technical parameters of test vehicle

試驗車輛上裝有OBD(On Board Diagnostics)車載終端，通過OBD對車輛行駛過程中行駛車速、行駛里程、時間、發動機輸出扭矩、地理位置等信息以1 Hz的頻率進行采集記錄。

1.2 數據預處理

在數據采集過程中可能會出現外界引號干擾、車輛顛簸導致數據采集出現噪聲或者傳輸錯誤。因此，將采集到的數據進行預處理，再對過濾后的數據進行工況構建。通過調查，高原地區道路車流量不大，服務水平高。結合高原地區汽車行駛特點，設定以下車速數據篩選條件：

(1)車速長時間(超過200 s)為0 km/h認為數據采集裝置與試驗車輛脫離，采集數據無效(試驗路段為公路，擁堵情況較少發生)。

(2)加速度超過5 m/s2認為加速度異常(平原地區汽車百公里加速時間為7 s左右，高原地區車輛動力性能會降低)。

(3)速度超過90 km/h為超速值(試驗道路設計速度80 km/h。但根據相關研究，路段限速80 km/h，道路服務水平較高時，駕駛員平均傾向速度為90 km/h左右[12])，進行剔除。

過濾后的部分速度與時間工況數據片段如圖1所示。

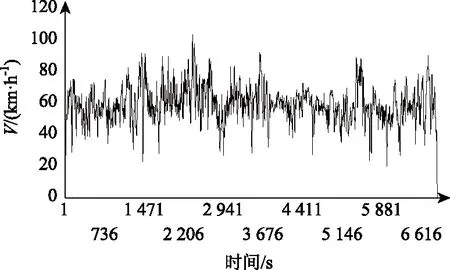
圖1 采集數據片段Fig.1 Collected data fragments

2 車速-時間工況構建

常用的汽車行駛工況構建方法有馬爾可夫鏈法、短行程法。

馬爾可夫鏈法：將采集數據按照統計學特征劃分為若干狀態，計算出各狀態的轉移概率矩陣，通過隨機數和轉移矩陣進行行駛工況構建[13-15]。

短行程法：將采集數據以怠速點劃分成若干運動學片段，然后再選取特征值，通過主成分分析，聚類方法進行典型行駛工況的構建[15-17]。

高原地區有高海拔、多山的地形特點，且交通量較少，交通處于自由流。汽車行駛過程中為了適應道路線形，需要不斷變化車速，導致怠速工況少，采用常規的短行程法不能構建出理想的行駛工況。

首先采用馬爾可夫鏈法進行高原山區行駛工況提取，并基于實際行駛工況特點，提出改進的短行程法：將采集數據按照固定時長劃分為若干片段，計算各個片段特征值，再進行主成分分析，通過聚類方法進行工況構建。

2.1 馬爾可夫鏈法

2.1.1 馬爾可夫特性的證明

“無后效應”是馬爾可夫鏈的典型特征。下一狀態的條件概率分布僅依賴于當前狀態，而與歷史狀態無關。假設汽車行駛過程中車速變化具有馬爾可夫特性，根據試驗數據分別構建不同時間間隔的子序列，理論上時間間隔越短，相關性越強[18]。分別采取1 s,5 s和10 s間隔進行車速馬爾可夫特性分析。

相關性圖可以直觀反映兩個變量相互影響的強弱。由圖2可知，當時間間隔為1 s時，采集數據呈現出強相關性，各點分布接近于一條直線；隨著時間間隔的增加，采樣點松散分布，變量之間的相關性逐漸減弱。為了量化第t秒車速與第t+s秒車速兩變量相關性，使用公式(1)皮爾遜相關系數進行計算,結果如表2所示。

(1)

式中，X為第t秒的車速；Y為第t+s秒的車速；s為時間間隔。

圖2 不同時間間隔下的車速相關性圖Fig.2 Correlation diagram of vehicle speed at different time intervals

由圖2和表2可知，車速的時間間隔越小，第t秒與第t+s秒的相關性越強。其中，時間間隔為1 s時第t秒的車速與第t+1秒的車速相關性系數達到0.990 3，且隨著時間間隔增加，逐漸失去相關性。綜上兩點，汽車行駛速度具有明顯的馬爾可夫特性，在研究中能夠采用馬爾可夫鏈法構建高原山區汽車行駛工況。

表2 不同時間間隔相關性系數Tab.2 Correlation coefficient of different time intervals

2.1.2狀態轉移矩陣的計算

車速從某一時刻某一狀態變化到下一時刻某一狀態，叫做狀態轉移，所有的狀態轉移組合在一起組成狀態轉移矩陣P，如公式(2)所示。

(2)

且狀態轉移矩陣具有如下特征：

(1)矩陣中每個元素均非負；

(2)矩陣中每行和為1。

先將采集數據進行狀態劃分，然后再根據相鄰兩點之間關系進行狀態模型事件頻率的統計，用頻率代替概率，如公式(3)所示。

(3)

式中，Nij為狀態i轉移到狀態j發生的頻數；pij為從狀態i轉移到狀態j的概率。

對預處理后的數據進行統計分析，得出汽車行駛車速主要分布在40～80 km/h區間內。將片段劃分為10個狀態(狀態1:v≤40 km/h,狀態2: 40 km/h80 km/h)。根據狀態轉移矩陣公式及狀態模型事件頻率得到狀態轉移矩陣P：

2.1.3馬爾可夫鏈法工況構建

(4)

圖3為Δ最小的片段，選擇其最后1 s的車速作為馬爾可夫初始狀態，v初始=53.254 km/h。

圖3 Δ值最小的片段Fig.3 Segment with smallest Δ value

將確定好的馬爾可夫初始狀態按照蒙特卡洛模擬法，通過狀態轉移矩陣進行工況構建。因為馬爾可夫鏈蒙特卡洛算法采用隨機數進行工況構建，即使初始狀態相同，也會構建出完全不同的行駛工況。本研究構建了10條行駛工況曲線，通過計算加速比例(Pa)、勻速比例(Pc)、減速比例(Pd)、平均速度(vm)、平均加速度(am)、速度標準偏差(vsd)、加速度標準偏差(asd)，選出與實際工況所有指標相對誤差之和最小的一條，如圖4所示。

圖4 馬爾可夫鏈法構建工況Fig.4 Driving cycle constructed by Markov chain method

2.2 改進的短行程法

2.2.1 特征值選取

根據高海拔地區道路線形設計規范和汽車行駛特點，將預處理后的數據按照50 s的時長劃分為若干運動學片段。選取加速比例(Pa)、勻速比例(Pc)、減速比例(Pd)、平均速度(vm)、平均加速度(am)、速度標準偏差(vsd)、加速度標準偏差(asd)為特征值。這些片段的特征值能夠詳細地描述汽車在高原地區的行駛特性，是構建典型工況的依據[17-19]。

2.2.2主成分分析

每個特征值都能夠提供一定的車輛道路行駛狀態信息，這些變量有的會包含部分重疊信息，即變量之間具有一定的相關性，相互之間不獨立。因此，可以通過主成分分析法簡化變量個數，以便于后續處理。

主成分分析法的基本思想是嘗試組合更多的原始變量，相互獨立地構建一些新的變量，并從實際的研究需求中選擇一些綜合變量[20]。通常，選擇80%或更多原始變量信息的線性組合可以簡化問題而不會忽略太多實際信息。

通過主成分分析法對特征值進行處理，得到各主成分貢獻率和累積貢獻率，如表3所示。

表3 各主成分貢獻率和累積貢獻率Tab.3 Contribution rate and cumulative contribution rate of each principal component

表3中Mi為各個主成分序號，特征值的大小反映主成分方差貢獻大小。前3個主成分累計貢獻率達到85.14%，且M1,M2,M3特征值均大于1，可以全面反映片段信息，達到了主成分分析的目的。

通過主成分分析結果繪制雙標圖如圖5所示。以提取出的前3個主成分為坐標軸，以中心為原點，將各變量在前3個主成分上的載荷用矢量線段表示，各矢量夾角的余弦值是它們的相關系數，余弦值越大，相關性越強。各片段在前3個主成分的得分情況可在雙標圖上顯示。

圖5 雙標圖Fig.5 Biplot

由圖5可知，第1主成分主要反映加速比例、勻速比例、速度標準差、加速度標準差等信息；第2主成分主要反映減速比例、平均加速度等信息；第3主成分主要反映平均速度等信息。

2.2.3k-means聚類

k-means聚類是一種簡潔高效的聚類算法，通過計算不同樣本間的距離判斷它們之間的相近關系，將具有相同特性的數據對象劃到同一類別中，與相關度較小的數據做以區分。基于各片段距各聚類中心的距離進行聚類[21-22]。

k-means聚類算法具體步驟如下：

(1)在主成分分析后的得分矩陣中選擇k個樣本點，將k個樣本點值分別作為k個初始聚類中心。

(2)依次計算各個樣本數據集中的所有數據點到各個初始聚類中心點的歐式距離，如公式(5)所示。

dij=|xi-μj|,

(5)

(3)迭代收斂

計算每個聚類的平均值，并作為新的中心點，重復上述過程，直到這k個中線點收斂了，輸出劃分結果。

圖6是聚類后的結果，將 138個樣本聚為3簇。

圖6 聚類結果Fig.6 Clustering result

第1簇有53個片段，第2簇有42個片段，第3簇有43個片段。將各運動學片段按照類別重新編號，并根據典型特征值進行分析，如圖7所示。第1簇加速工況占比最大，為加速路段；第2簇勻速工況占比最大，為勻速路段；第3簇的3種工況占比差別不大，分析為試驗車輛行駛路段線形復雜，駕駛員需要不斷變化車速以適應道路變化。

圖7 聚類結果分析Fig.7 Cluster result analysis

根據各片段到聚類中心的距離大小，按照運動學片段原始序號，第1簇選擇片段63，36，50，68，127，23；第2簇選擇片段129，77，102，108，97；第3簇選擇片段74，31，76，25，41。將所選片段按照時間順序進行工況構建。

在工況構建過程中，可能會出現車速較大的點與車速較小的點相連接，導致加減速強度過大或加速度數值異常。對這些點采取中位值平均濾波法進行濾波：以加速度異常值處為中心，選擇14個前后相鄰點，去掉這些點中的速度最大值和速度最小值，用剩余點的平均速度代替加速度數值異常處的點，并控制連續加速時間。構建工況如圖8所示。

圖8 改進的短行程法構建工況Fig.8 Driving cycle constructed by improved short stroke method

3 對比分析

將馬爾可夫鏈法構建高原山區典型行駛工況1和改進的短行程法構建的高原山區典型行駛工況2與實際工況進行對比，如表4、表5所示：

表4 構建行駛工況1與實際工況對比Tab.4 Comparison between constructed driving cycle 1 and actual driving cycle

表5 構建行駛工況2與實際工況對比Tab.5 Comparison between constructed driving cycle 2 and actual driving cycle

由表4、表5可知，馬爾可夫鏈法構建工況的特征值與實際工況偏差較大，其中，勻速工況誤差最大。分析原因為狀態轉移矩陣主對角線數值最大，即通過馬爾可夫鏈法構建的行駛工況偏向于車輛穩定行駛工況，這一特點與城市工況較為符合；改進的短行程法構建工況車速變化復雜，特征值與實際工況特征值誤差較小，能夠較好地擬合高原山區汽車行駛工況。

將馬爾可夫鏈法與改進的短行程法構建的工況進行對比，如圖9所示。馬爾可夫鏈方法構建的高原地區行駛工況較為平穩，車速變化幅度及頻率較小；改進的短行程法構建的行駛工況車速變化頻繁，與高海拔地區多山的道路環境特征相符。

圖9 構建工況對比Fig.9 Comparison of constructed driving cycles

4 結論

本研究以川藏線道路采集工況數據為研究對象提出了構建高原山區乘用車行駛工況的方法。

(1)通過不同時間間隔證明汽車行駛工況具有馬爾可夫特性。根據馬爾可夫蒙特卡洛法構建的高原山區行駛工況較為平穩，以勻速工況為主，車速變化幅度及頻率較小。

(2)用改進的短行程法按照50 s的固定時長將汽車行駛工況劃分為138個運動學片段，通過主成分分析，k-means聚類構建行駛工況，并通過中位值平均濾波法進行異常點的濾波。改進的短行程法構建的行駛工況加速，減速的波動變化較為頻繁，

(3)通過比較指標(加速比例、勻速比例、減速比例、平均速度、平均加速度、速度標準偏差、加速度標準偏差)，將兩種方法構建的行駛工況與實際工況對比，發現用改進的短行程法構建的行駛工況誤差較小，可以反映高原山區車輛行駛特點，這為研究行駛工況提供了新思路。