基于車-橋耦合動(dòng)力作用的車輛與橋梁力學(xué)行為

郝艷廣，袁龍文，韓勁龍，梁濟(jì)川，歐陽(yáng)彪

(1. 中交二航局建筑科技有限公司, 湖北 武漢 430000; 2. 海工結(jié)構(gòu)新材料及維護(hù)加固技術(shù)湖北省重點(diǎn)實(shí)驗(yàn)室, 湖北 武漢 430040;3. 廣東省北江航道開(kāi)發(fā)投資有限公司, 廣東 清遠(yuǎn) 511500)

0 引言

車-橋耦合動(dòng)力作用包括大量非線性因素，如橡膠輪胎大變形、瀝青混合料黏彈性、路面不平度等[1-2]。橋面鋪裝層分層鋪筑，各層材料在環(huán)境變化和車-橋耦合動(dòng)力作用下出現(xiàn)大量病害，如瀝青混合料推移、脫落、車轍等,水泥混凝土裂縫、破損等,鋼板、鋼梁焊接處銹蝕等。這些病害嚴(yán)重影響橋梁工作狀態(tài)以及服役壽命，相關(guān)問(wèn)題亟待解決[3-4]。

車輛與橋梁相關(guān)參數(shù)、路面不平度激勵(lì)以及車橋工作狀態(tài)對(duì)車-橋力學(xué)行為有巨大影響[5]。國(guó)內(nèi)外學(xué)者針對(duì)車-橋耦合動(dòng)力作用已進(jìn)行大量研究：張彥玲等[6]研究橋梁在諧波荷載作用下力學(xué)行為，結(jié)果表明橋梁跨中動(dòng)撓度受靜載影響較大。魏志剛等[7]推導(dǎo)車輛動(dòng)載作用下橋梁剛度分布函數(shù)，根據(jù)變形協(xié)調(diào)方程及荷載平衡條件，得到橋梁動(dòng)力響應(yīng)。張玥等[8]基于Midas/FEA軟件，建立橋梁模型，研究不同工況下橋梁應(yīng)力變化規(guī)律。李慧樂(lè)等[9]建立三維車輛模型與橋梁有限元模型，根據(jù)車輛與橋梁接觸行為，求解橋梁動(dòng)態(tài)響應(yīng)。楊永清等[10]建立某公路橋正交異性橋面板有限元模型，研究其在移動(dòng)荷載下不同橋梁部位應(yīng)力特征，并基于應(yīng)力等效原則建立足尺模型驗(yàn)證不同橋梁部位疲勞特性。綜上可知，大量車-橋耦合動(dòng)力研究采用移動(dòng)荷載、移動(dòng)質(zhì)量塊或者簧上質(zhì)量模擬車輛荷載；橋面鋪裝層材料未能考慮瀝青混合料黏彈性；輪胎簡(jiǎn)化為質(zhì)量、剛度、阻尼模型，相關(guān)研究結(jié)果與工程實(shí)際存在較大差距。

建立四分之一車輛模型和簡(jiǎn)支橋模型，其中車輛模型考慮橡膠輪胎，簡(jiǎn)支橋模型考慮瀝青混合料黏彈性。基于輪胎與橋面鋪裝層接觸關(guān)系，建立車-橋耦合動(dòng)力模型，采用中心差分法和有限元理論求解車-橋耦合動(dòng)力方程以及車輛與橋梁時(shí)域響應(yīng),將仿真值與測(cè)量值進(jìn)行對(duì)比，驗(yàn)證該模型。計(jì)算分析橋面鋪裝層三向應(yīng)力狀態(tài)以及不同路面不平度激勵(lì)下車輛和橋梁力學(xué)行為，以期為車輛和橋梁設(shè)計(jì)提供一定理論依據(jù)。

1 四分之一車輛模型

車輛是復(fù)雜多自由度系統(tǒng)，一般由車體、懸架、輪胎構(gòu)成。基于多體動(dòng)力學(xué)理論，在ABAQUS中建立四分之一車輛有限元模型，其中車體假設(shè)為均質(zhì)剛體，輪胎采用橡膠材料模擬。利用連接器將兩輪胎分別耦合并采用連接器Hinge屬性，模擬車軸；利用連接器將車體與車軸連接并采用連接器Cartesian屬性，車輛有限元模型及力學(xué)模型如圖1所示，相關(guān)參數(shù)如表1所示。

圖1 車輛有限元模型與力學(xué)模型Fig.1 FE model and mechanical model of vehicle

表1 車輛參數(shù)Tab.1 Parameters of vehicle

2 橡膠輪胎模型

相關(guān)研究中，輪胎模型均采用如下假設(shè)：輪胎由質(zhì)量、剛度和阻尼構(gòu)成，根據(jù)D′alember原理列出微分方程，并進(jìn)行求解。實(shí)際輪胎是由橡膠基體、簾布層、鋼絲簾線等多種材料壓制而成。為保證計(jì)算精度并提高計(jì)算效率，建立橡膠輪胎有限元模型并進(jìn)行適當(dāng)簡(jiǎn)化，保留胎側(cè)與胎面、胎體等橡膠材料以及骨架材料。利用CAD繪制輪胎斷面圖，導(dǎo)入ABAQUS中生成輪胎有限元模型。輪胎斷面圖、各部分有限元模型以及相關(guān)網(wǎng)格劃分如圖2所示。

圖2 輪胎模型Fig.2 Model of tire

ABAQUS包含Mooney-Rivlin模型、Yeoh模型、Neo-Hookean模型等本構(gòu)模型，各模型均具有獨(dú)特性質(zhì)，針對(duì)不同問(wèn)題，選擇適當(dāng)模型。Yeoh模型適用于描述橡膠材料大變形，本研究采用Yeoh模型。

橡膠具有體積不可壓縮非線性力學(xué)特點(diǎn)，是三維正交各項(xiàng)異性復(fù)合結(jié)構(gòu)物[11]。基于應(yīng)力-應(yīng)變關(guān)系以及唯象理論建立橡膠材料本構(gòu)關(guān)系，采用體應(yīng)變能表征其力學(xué)特性，其方程如下：

W=W(I1,I2,I3)，

(1)

(2)

(3)

Eij=(λ1λ2)2+(λ2λ3)2+(λ3λ1)2，

(4)

I3=(λ1λ2λ3)2，

(5)

λ=1+γi，

(6)

式中，W為體應(yīng)變能；I1，I2，I3分別為左Cauchy-green第一、第二、第三張量不變量，當(dāng)I3=1時(shí)，橡膠材料不可壓縮；γi為主應(yīng)變；1，2，3下角標(biāo)為相互垂直方向，橡膠材料只有單向拉伸，則λ1·λ2·λ3=1；對(duì)于橡膠材料，?W/?I2遠(yuǎn)小于?W/?I1，一般認(rèn)為?W/?I2在應(yīng)變能中貢獻(xiàn)度很小，可以忽略，則應(yīng)變能函數(shù)簡(jiǎn)化為[11-13]

(7)

式中Cij為橡膠輪胎材料參數(shù)。

橡膠材料參數(shù)來(lái)自文獻(xiàn)[14]，見(jiàn)表2。

表2 橡膠輪胎參數(shù)[14]Tab.2 Parameters of rubber tire[14]

橡膠輪胎主要結(jié)構(gòu)有帶束層、胎體簾線、鋼絲簾線、鋼絲圈等。利用Rebar單元模擬鋼絲簾線結(jié)構(gòu)。橡膠材料是輪胎主要成分，采用CGAX4H單元和CGAX3H單元模擬二維橡膠材料，并經(jīng)空間旋轉(zhuǎn)成三維立體模型，相應(yīng)單元類型改變?yōu)镃3D8H單元和C3D6H單元[15]。

3 簡(jiǎn)支橋模型

簡(jiǎn)支橋來(lái)自江西省某高速公路，全長(zhǎng)24 m，采用4塊縱向工字鋼、21塊橫向工字鋼以及橋面板焊接而成。縱梁高1.6 m，間距3 m，縱梁梁頂與橋面板底面焊接；橫梁高0.4 m，間距4 m，橫梁梁端與縱梁側(cè)面焊接。縱梁、橫梁、橋面板均采用Q345鋼，橋面鋪裝層相關(guān)材料參數(shù)如表3、表4所示。

圖3 簡(jiǎn)支橋模型Fig.3 Model of simply supported bridge

表3 橋面鋪裝層材料參數(shù)Tab.3 Material parameters of deck pavement

水泥混凝土采用線彈性本構(gòu)模型；瀝青混合料具有黏彈性，采用廣義Maxwell模型模擬，廣義Maxwell模型如圖4所示。

圖4 廣義Maxwell模型Fig.4 Generalized Maxwell model

對(duì)廣義Maxwell模型施加一定應(yīng)變，每一個(gè)Maxwell元件均有同樣應(yīng)變，則：

σi=ε0Eiexp(-t/τi)，

(8)

總應(yīng)力為:

(9)

則松弛模量函數(shù)為:

(10)

當(dāng)t=0時(shí)

(11)

式中，E0為初始松弛模量；Ee為松弛時(shí)間t無(wú)窮時(shí)刻平衡值；σ(t)為應(yīng)力；ε0為初應(yīng)變。

廣義Maxwell高分子聚合物經(jīng)典遺傳積分形式可以寫(xiě)成:

(12)

式中，σ0(s)為彈性響應(yīng)部分；g(t)為衰減函數(shù)，采用Prony級(jí)數(shù)表示：

(13)

瀝青混合料黏彈性參數(shù)來(lái)自文獻(xiàn)[16]。

表4 黏彈性參數(shù)[16]Tab.4 Parameters of viscoelasticity[16]

4 車-橋耦合動(dòng)力模型

4.1 路面不平度

路面不平度是車-橋耦合振動(dòng)主要原因，由《機(jī)械振動(dòng)道路路面譜測(cè)量數(shù)據(jù)報(bào)告》(GB/T 7031—2005/ISO 8608: 1995)可得路面功率譜表達(dá)式為

Gq(n)=Gq(n0)|n/n0|-ω,

(14)

式中，n0=0.1 m-1，為空間參考頻率；n為任意有效空間頻率；Gq(n0)為參考空間頻率對(duì)應(yīng)的功率譜密度，B級(jí)路面取64×10-6m2/m-1；ω為頻率指數(shù)，用于確定路面不平度的頻率結(jié)構(gòu)，通常取2。B級(jí)路面不平度如圖5所示。

圖5 B級(jí)路面不平度Fig.5 Class B pavement roughness

4.2 接觸關(guān)系

輪胎與橋面接觸關(guān)系可分為法向接觸行為和切向接觸行為。法向接觸行為采用“硬接觸”表示，并通過(guò)罰函數(shù)計(jì)算法向力:

(15)

式中，kn為法向接觸剛度；C為間隙值。

切向接觸行為采用庫(kù)倫摩擦力表示，摩擦力數(shù)值取決于輪胎與路面接觸狀態(tài)

(16)

式中，kt為切向剛度；ne為接觸節(jié)點(diǎn)相對(duì)變形；μ為摩擦系數(shù)。

4.3 邊界條件

約束橋梁兩端相關(guān)自由度，模擬簡(jiǎn)支橋邊界條件。為保證橡膠輪胎自由滾動(dòng)，對(duì)連接器施加沿z方向平動(dòng)速度。橋面設(shè)置摩擦系數(shù)μ，輪胎與橋面之間摩擦力推動(dòng)輪胎滾動(dòng)，如圖6所示。

圖6 輪胎旋轉(zhuǎn)示意圖Fig.6 Schematic diagram of tire rotation

4.4 求解車-橋耦合動(dòng)力方程

車-橋耦合動(dòng)力模型分為車輛模型和橋梁模型，基于有限元理論將車輛、橋梁模型分別離散，如圖7所示。

圖7 車-橋耦合動(dòng)力模型Fig.7 Vehicle-bride coupling dynamic model

通過(guò)輪胎-橋面接觸關(guān)系實(shí)現(xiàn)兩模型之間力學(xué)關(guān)系轉(zhuǎn)換。路面不平度作為外部激勵(lì)，形成車-橋耦合，其耦合效應(yīng)隨路面平整度降低而加劇[17-20]。接觸理論將輪胎與橋面接觸關(guān)系轉(zhuǎn)換成時(shí)域上連續(xù)接觸關(guān)系，則車-橋耦合動(dòng)力方程為:

(17)

式中，Y″，Y′，Y分別為加速度、速度、位移向量；M，C，K分別為質(zhì)量、阻尼、剛度矩陣；下角標(biāo)v，r分別表示車輛和橋梁；Rv，Rr分別為車輛與橋梁恢復(fù)力；Pvr，Prv分別為車輛與橋梁之間作用力。

所建模型考慮輪胎與橋面之間摩擦以及多種非線性材料，導(dǎo)致耦合動(dòng)力方程中阻尼矩陣和剛度矩陣為非對(duì)稱矩陣。針對(duì)這一問(wèn)題，擬采用中心差分法求解。中心差分法每一時(shí)間步積分步長(zhǎng)可由下式確定:

(18)

式中，Tn為有限元模型最小固有頻率。加速度和速度分別為:

(19)

(20)

將式(19)和式(20)代入式(17)，可求得每個(gè)時(shí)間步位移。由有限元理論可知，位移與應(yīng)變存在如下關(guān)系

εe=BYe，

(21)

σe=Dεe，

(22)

σe=DBYe，

(23)

式中，εe為單元應(yīng)變；σe為單元應(yīng)力；Y為單元節(jié)點(diǎn)位移；B為位移-應(yīng)變關(guān)系矩陣；D為彈性矩陣。

綜上所述，建立車-橋耦合動(dòng)力方程，并基于中心差分法和有限元理論求解，可得車-橋耦合動(dòng)力作用下時(shí)域響應(yīng)，如位移、應(yīng)力等。

5 力學(xué)行為分析

5.1 模型驗(yàn)證

為驗(yàn)證所建模型可行性，將上面層跨中豎向應(yīng)力仿真值與測(cè)量值進(jìn)行比較。待中面層瀝青混合料鋪設(shè)完成后，在橋梁跨中截面布設(shè)土壓力盒以及連接導(dǎo)線，然后鋪設(shè)上面層瀝青混合料。相關(guān)施工工序完成后，進(jìn)行車-橋耦合測(cè)量試驗(yàn)，測(cè)量車輛動(dòng)載作用下橋面鋪裝層應(yīng)力變化狀態(tài)。土壓力盒布設(shè)如圖8所示，對(duì)比結(jié)果如圖9所示，速度取30 m/s。

圖8 土壓力盒布設(shè)示意圖Fig.8 Schematic diagram of layout of earth pressure boxes

圖9 上面層豎向應(yīng)力Fig.9 Vertical stress of upper surface layer

由圖9可知，車輛動(dòng)載作用下，上面層跨中豎向應(yīng)力仿真值為0.608 MPa，測(cè)量值為0.630 MPa，比仿真值大3.618%，表明基于相關(guān)理論構(gòu)建車-橋耦合動(dòng)力模型具有一定可行性，相關(guān)計(jì)算方法恰當(dāng)。

5.2 鋪裝層三向應(yīng)力

以橋面鋪裝層跨中為觀測(cè)點(diǎn)，提取該點(diǎn)三向應(yīng)力時(shí)程曲線，分析車輛動(dòng)載作用下橋面鋪裝層動(dòng)力響應(yīng)。

圖10 橋面鋪裝層豎向應(yīng)力Fig.10 Vertical stress of bridge deck pavement

由圖10可知，車輛動(dòng)載作用下，橋面鋪裝層豎向應(yīng)力以受壓為主，上、中、下面層最大豎向壓應(yīng)力分別為0.608，0.507，0.330 MPa，豎向壓應(yīng)力隨橋面鋪裝層深度增加逐漸降低。

由圖11可知，車輛動(dòng)載作用下，橋面鋪裝層橫向應(yīng)力以受壓為主，并呈現(xiàn)出一定的振動(dòng)形態(tài)。上、中、下面層最大橫向壓應(yīng)力分別為0.283，0.245，0.227 MPa，橫向壓應(yīng)力隨橋面鋪裝層深度增加逐漸減小。

圖11 橋面鋪裝層橫向應(yīng)力Fig.11 Transverse stress of bridge deck pavement

由圖12可知，車輛動(dòng)載作用下，橋面鋪裝層縱向應(yīng)力以受壓為主，上、中、下面層最大縱向壓應(yīng)力分別為0.338，0.277，0.245 MPa，縱向壓應(yīng)力隨橋面鋪裝層深度增加逐漸減小。

圖12 橋面鋪裝層縱向應(yīng)力Fig.12 Longitudinal stress of bridge deck pavement

5.3 路面不平度對(duì)力學(xué)行為影響

本研究構(gòu)建B級(jí)路面不平度，探究路面不平度激勵(lì)對(duì)橋面鋪裝層、鋼橋部件以及車輛動(dòng)態(tài)響應(yīng)影響規(guī)律。

5.3.1上面層跨中

由圖13可知，添加B級(jí)路面不平度，上面層跨中最大豎向壓應(yīng)力為1.327 MPa，比未添加不平度增大118.257%。

圖13 不同路面等級(jí)上面層豎向應(yīng)力Fig.13 Vertical stress of upper surface layer in different road grades

由圖14可知，添加B級(jí)路面不平度，上面層跨中最大橫向壓應(yīng)力為0.652 MPa，比未添加不平度增大130.389%，且橫向應(yīng)力時(shí)程曲線振動(dòng)形態(tài)加劇。

圖14 不同路面等級(jí)上面層橫向應(yīng)力Fig.14 Transverse stress of upper surface layer in different road grades

由圖15可知，添加B級(jí)路面不平度，上面層跨中最大縱向壓應(yīng)力為0.706 MPa，比未添加不平度增大108.876%，且縱向應(yīng)力時(shí)程曲線呈現(xiàn)出波動(dòng)狀態(tài)。

圖15 不同路面等級(jí)上面層縱向應(yīng)力Fig.15 Longitudinal stress of upper surface layer in different road grades

5.3.2鋼板頂面

由圖16可知，未添加路面不平度，鋼板頂面跨中最大豎向壓應(yīng)力為0.012 MPa；添加B級(jí)路面不平度為0.027 MPa，比未添加不平度增大125%。

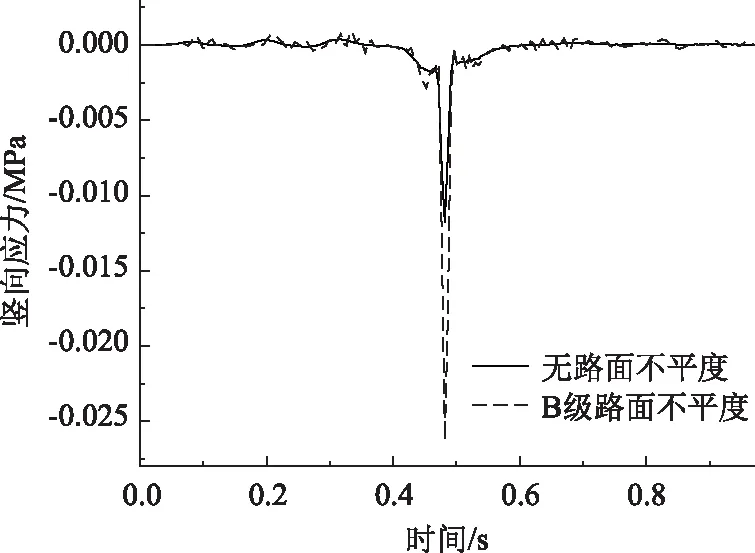
圖16 不同路面等級(jí)鋼板頂面豎向應(yīng)力Fig.16 Vertical stress of top surface of steel plate in different road grades

由圖17可知，未添加不平度，鋼板頂面跨中最大橫向拉應(yīng)力為1.290 MPa；添加B級(jí)路面不平度為2.210 MPa，比未添加不平度增大71.318%，且橫向應(yīng)力時(shí)程曲線振動(dòng)加劇。

圖17 不同路面等級(jí)鋼板頂面橫向應(yīng)力Fig.17 Transverse stress of top surface of steel plate in different road grades

由圖18可知，未添加不平度；鋼板頂面跨中最大縱向拉應(yīng)力為0.793 MPa；添加B級(jí)路面不平度為2.030 MPa，比未添加不平度增大155.990%。

圖18 不同路面等級(jí)鋼板頂面縱向應(yīng)力Fig.18 Longitudinal stress of top surface of steel plate in different road grades

5.3.3車輛懸架

由圖19和圖20可知，添加B級(jí)路面不平度，車輛懸架彈力與阻尼力均增大，車輛振動(dòng)明顯，車-橋耦合動(dòng)力效應(yīng)增強(qiáng)。未添加不平度，最小和最大車輛懸架彈力分別為36.178，59.322 kN，變化幅度為63.973%；添加B級(jí)路面不平度，最小和最大懸架彈力分別為33.738，60.859 kN，變化幅度為80.387%。

圖19 不同路面等級(jí)車輛懸架彈力Fig.19 Elastic force of vehicle suspension in different road grades

圖20 不同路面等級(jí)懸架阻尼力Fig.20 Damping force of vehicle suspension in different road grades

5.3.4縱梁跨中

由圖21可知，未添加不平度，縱梁跨中最大豎向拉應(yīng)力為0.105 MPa，最大豎向壓應(yīng)力為0.282 MPa；添加B級(jí)路面不平度，縱梁跨中最大豎向拉應(yīng)力為0.209 MPa，最大豎向壓應(yīng)力為0.449 MPa，分別比未添加不平度增大99.048%、59.220%。

圖21 不同路面等級(jí)縱梁豎向應(yīng)力Fig.21 Vertical stress of vertical beam in different road grades

由圖22可知，未添加不平度，縱梁跨中最大橫向拉應(yīng)力為0.167 MPa，最大橫向壓應(yīng)力為0.193 MPa；添加B級(jí)路面不平度，縱梁跨中最大橫向拉應(yīng)力為0.365 MPa，最大橫向壓應(yīng)力為0.418 MPa，分別比未添加不平度增大118.563%,116.580%。

圖22 不同路面等級(jí)縱梁橫向應(yīng)力Fig.22 Transverse stress of vertical beam in different road grades

由圖23可知，未添加不平度，縱梁跨中最大縱向拉應(yīng)力為0.046 MPa，最大縱向壓應(yīng)力為0.159 MPa；添加B級(jí)路面不平度，縱梁跨中最大縱向拉應(yīng)力為0.309 MPa，最大縱向壓應(yīng)力為0.348 MPa，分別比未添加不平度增大245.652%,118.868%。

圖23 不同路面等級(jí)縱梁縱向應(yīng)力Fig.23 Longitudinal stress of vertical beam in different road grades

由以上分析可知，車輛動(dòng)載作用下，縱梁跨中三向應(yīng)力均以受壓為主。受不平度以及車輛振動(dòng)影響，當(dāng)車輛接近或遠(yuǎn)離觀測(cè)點(diǎn)時(shí)，縱梁跨中三向應(yīng)力均表現(xiàn)出一定拉應(yīng)力。橋面鋪裝層為B級(jí)路面不平度時(shí)，三向應(yīng)力極值均增大，且應(yīng)力時(shí)程曲線呈現(xiàn)出一定波動(dòng)狀態(tài)，應(yīng)力狀態(tài)復(fù)雜。

6 結(jié)論

本研究建立兩自由度四分之一車輛模型和簡(jiǎn)支橋模型，將橋面鋪裝層上面層跨中豎向應(yīng)力仿真值與測(cè)量值對(duì)比，驗(yàn)證該模型,進(jìn)一步分析橋面鋪裝層三向應(yīng)力狀態(tài)以及不同路面等級(jí)下各項(xiàng)力學(xué)行為變化規(guī)律。結(jié)果表明：

(1)車輛動(dòng)載作用下，上面層跨中豎向應(yīng)力測(cè)量值比仿真值大3.618%，表明所建車-路耦合動(dòng)力模型具有一定可行性。

(2)車輛動(dòng)載作用下，三向壓應(yīng)力隨橋面鋪裝層深度增加逐漸降低。

(3)橋面鋪裝層為B級(jí)路面時(shí)，車-橋耦合效應(yīng)增強(qiáng)，車輛與橋梁各項(xiàng)響應(yīng)均增大。在橋梁運(yùn)營(yíng)期間應(yīng)嚴(yán)格控制路面不平度，防止車輛以及橋梁耦合振動(dòng)效應(yīng)加劇。

(4) 因現(xiàn)場(chǎng)試驗(yàn)條件有限，無(wú)法保證改變車輛重量后相關(guān)測(cè)量數(shù)據(jù)的準(zhǔn)確性，故只進(jìn)行了車輛滿載工況下，相關(guān)動(dòng)力響應(yīng)的測(cè)試與分析，并建立該工況有限元模型，驗(yàn)證其正確性。在后續(xù)研究中，將考慮多種工況，為理論分析提供更全面的參考。