小學(xué)數(shù)學(xué)理學(xué)案的核心要素與編制原則
[摘 要]理學(xué)案是“至理數(shù)學(xué)”教學(xué)主張在課堂落地生根的有效載體,其核心要素包括學(xué)材分析、學(xué)情調(diào)研、理學(xué)目標、理學(xué)歷程。理學(xué)案在編制時需要遵循一體化、一致性、易操作等原則。
[關(guān)鍵詞]理學(xué)案;核心要素;編制原則
[中圖分類號] G623.5[文獻標識碼] A[文章編號] 1007-9068(2021)08-0001-04
一、理學(xué)案的內(nèi)涵與結(jié)構(gòu)
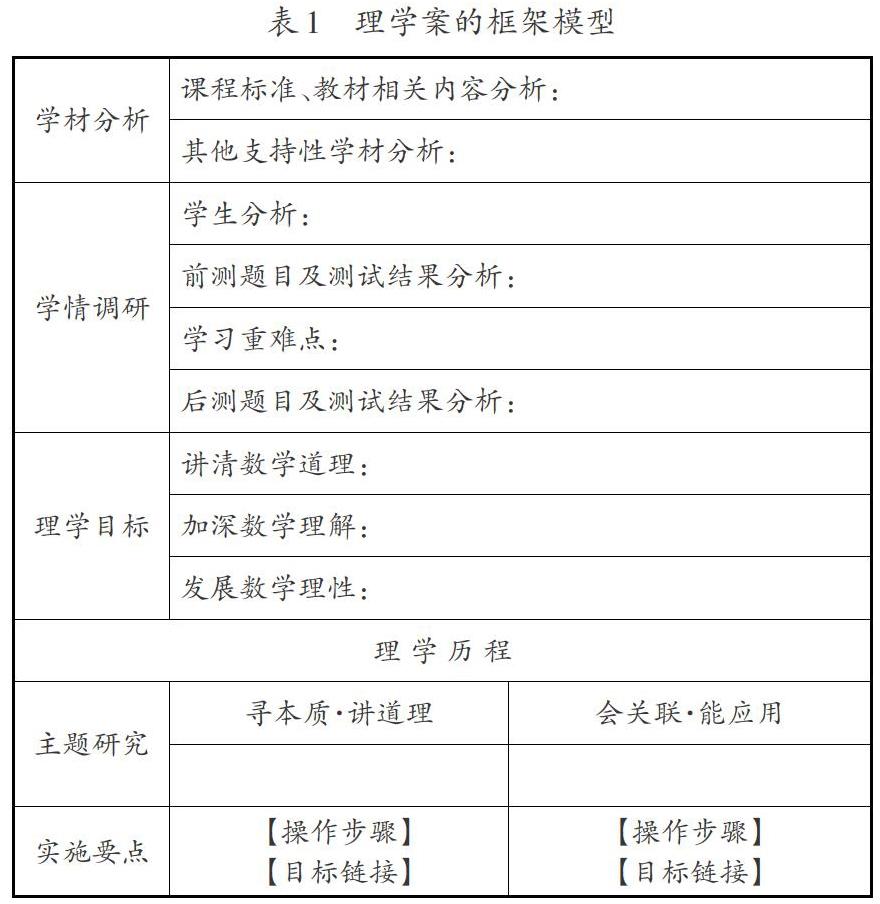
“至理數(shù)學(xué)”是一種堅持從兒童出發(fā),堅守學(xué)科本質(zhì)和素養(yǎng)本真的教學(xué)主張,理學(xué)案是該教學(xué)主張在課堂落地生根的有效載體。理學(xué)案是在深度學(xué)習(xí)和踐行學(xué)歷案的基礎(chǔ)上發(fā)展而來的。理學(xué)案是教師站在學(xué)生的立場,通過深度挖掘與教材相關(guān)的知識本質(zhì)、學(xué)科本質(zhì)設(shè)計出一個或幾個具有主題性的研究任務(wù),促使學(xué)生自主學(xué)習(xí),逐步達到“學(xué)會”和“理解”的教、學(xué)一體化方案。它從學(xué)習(xí)者的視角,以“學(xué)什么”“怎么學(xué)”“學(xué)得怎么樣”來設(shè)計學(xué)習(xí)過程。一份完整的理學(xué)案包括學(xué)材分析、學(xué)情調(diào)研、理學(xué)目標、理學(xué)歷程四個核心要素,其結(jié)構(gòu)詳見表1。
本文以小學(xué)數(shù)學(xué)理學(xué)案設(shè)計為切入點,結(jié)合蘇教版教材五年級下冊“圓的面積”一課(以下簡稱“圓的面積”),重點分析其四個核心部分。
二、理學(xué)案的核心要素
1.學(xué)材分析
“至理數(shù)學(xué)”教學(xué)主張下的學(xué)材分析不僅包括課程標準、教材相關(guān)內(nèi)容分析,還可以對其他支持性學(xué)材進行分析。本文學(xué)材分析主要就前兩者展開。
《義務(wù)教育數(shù)學(xué)課程標準(2011年版)》關(guān)于“圓的面積”的表述極其簡練——探索并掌握圓的面積公式,并能解決簡單的實際問題,與之匹配的蘇教版教材將“圓的面積”安排在五年級下冊進行學(xué)習(xí)。雖然學(xué)生之前已經(jīng)學(xué)過長方形、正方形、平行四邊形、三角形和梯形的基本特征及其周長、面積計算公式,對圓的特征、周長也有一定的認識,但因為“圓的面積”需將曲線圖形轉(zhuǎn)化成直線圖形,且涉及極限思想,所以認知難度較大。為了幫助學(xué)生有效突破學(xué)習(xí)難點,教材安排了兩個例題,例1是探索圓的面積與以它的半徑為邊長的正方形面積之間的近似關(guān)系,例2是將圓轉(zhuǎn)化成已經(jīng)學(xué)過的平行四邊形和長方形來探索圓的面積公式。不難看出,教材希望從“數(shù)方格”開始,讓學(xué)生先整體感知圓的面積和半徑平方之間的關(guān)系,再通過操作對圓的面積公式進行推理和驗證。
2.學(xué)情調(diào)研
學(xué)情調(diào)研是理學(xué)案的重要組成部分,它是設(shè)定理學(xué)目標、設(shè)計和實施主題研究任務(wù)的主要依據(jù)。作為一種教育技術(shù)手段,理學(xué)案的學(xué)情調(diào)研比一般的學(xué)情調(diào)研要求更加細致、深刻、靈活:在內(nèi)容上,需要涉及學(xué)生原有的知識儲備、生活經(jīng)驗,必要時學(xué)習(xí)習(xí)慣與學(xué)習(xí)品質(zhì)也可涵蓋其中;在形式上,一般采用問卷、訪談等形式進行了解,必要時也可通過資料研究、課堂觀察等加以完善;在時間上,可以根據(jù)需要放在課前、課中或是課后進行,課前測試便于了解真實起點,課中觀察便于把握學(xué)習(xí)狀態(tài),課后測試便于檢驗學(xué)習(xí)效果;從對象上,可以面向全體施教學(xué)生,也可選擇不同層次的學(xué)生代表;從結(jié)論上,需要點、面結(jié)合,既要對全班學(xué)生進行整體分析,也要對學(xué)生個體精準把握,以形成“面向全體、關(guān)注差異”的教學(xué)策略和矯正措施。
為了解學(xué)生的已有經(jīng)驗和學(xué)習(xí)起點,我們設(shè)計了前測題目:
1.憶一憶:你學(xué)過哪些平面圖形?用字母寫出它們的面積公式。
2.想一想:這些平面圖形的面積公式是怎么得到的?選擇一個,寫出它的研究過程。
你選擇的是(? ? ? ?)形。
研究過程:
3.關(guān)于圓的面積:
(1)你知道圓的面積公式嗎?(在括號內(nèi)畫“√”)? 知道(? ? )?不知道(? ? )
如果知道,請寫出面積公式:
(2)你知道圓的面積是怎么得到的嗎?(在括號內(nèi)畫“√”)
知道(? ? )?不知道(? ? )
如果知道,請寫出研究過程:
為了不加重師生負擔(dān),但又能確保調(diào)研結(jié)果的典型性和代表性,我們分別從授課班級中的 “中上”“中等”“中下”水平的學(xué)生中隨機抽取各4人參與測試和訪談。前測數(shù)據(jù)顯示,對于第1題(考查已學(xué)圖形面積公式),80%以上的學(xué)生都能寫出3種以上的圖形名稱及其面積公式,但大多不會使用字母表達,而直接寫成如“長×寬”的形式,還有混淆面積和周長公式的情況。對于第2題(考查已學(xué)圖形面積公式來源),半數(shù)以上的學(xué)生寫出了“轉(zhuǎn)化”,其余學(xué)生或留空,或文不對題;而在舉例說明面積研究方法時,學(xué)生選擇較多的是將平行四邊形轉(zhuǎn)化成長方形來研究面積,三角形次之,梯形最少,而用小正方形拼擺得到長方形面積,即“數(shù)格子”的方法,無人提及。對于第3題(考查新知),有4人知道圓的面積公式,但能寫出研究過程的只有1人,他是把圓轉(zhuǎn)化成近似平行四邊形后進行推導(dǎo),由訪談得知,其法為校外培訓(xùn)班所教。由上可知,多數(shù)學(xué)生對以前學(xué)習(xí)的平面圖形面積公式尚有記憶,對四年級研究平行四邊形面積所用的“轉(zhuǎn)化”方法印象較深,對三年級研究長方形面積公式的“數(shù)格子”方法遺忘嚴重,對四年級所學(xué)的三角形、梯形面積公式來源遺忘程度次之;對于即將學(xué)習(xí)的新知,大部分學(xué)生缺乏技術(shù)儲備。此次調(diào)研雖然程序簡易,但深入和全面,能幫助教師精準判斷學(xué)生“在哪里”和選擇“何以學(xué)會”的最佳路徑。
3.理學(xué)目標
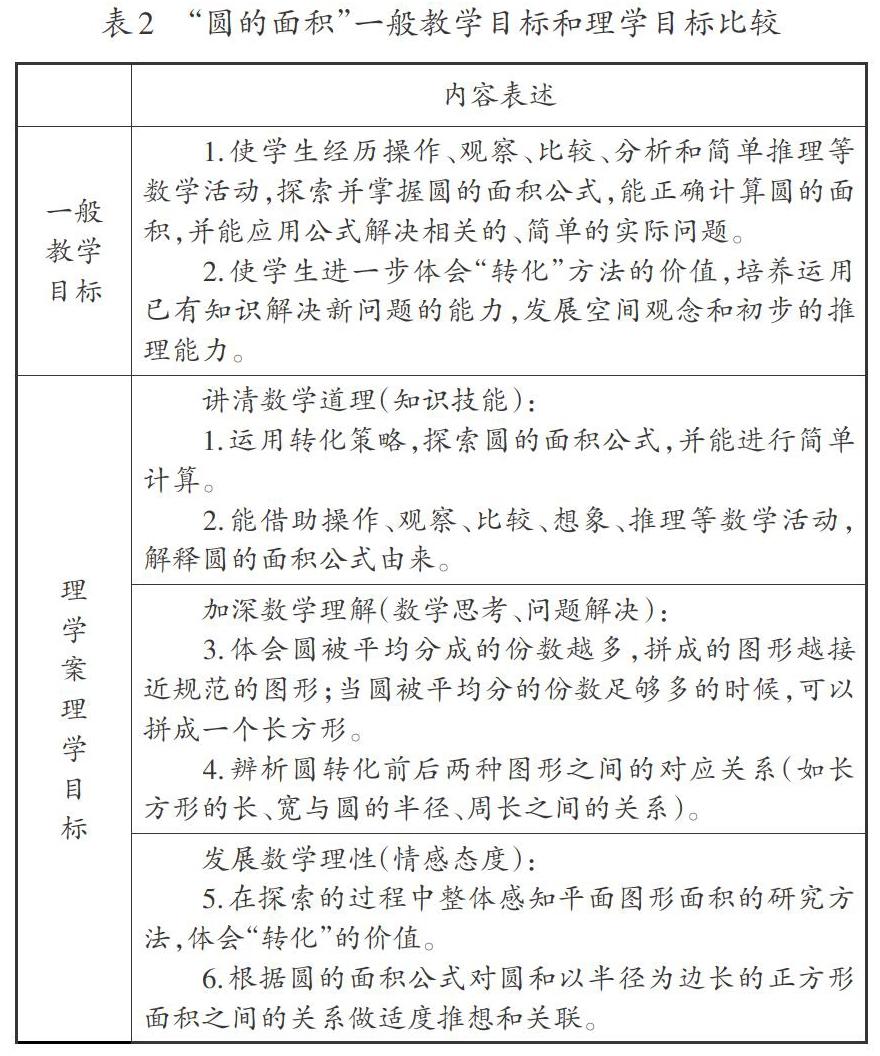
《義務(wù)教育數(shù)學(xué)課程標準(2011年版)》從“知識技能”“數(shù)學(xué)思考”“問題解決”“情感態(tài)度”四個方面闡述教學(xué)目標。理學(xué)目標結(jié)合教學(xué)主張本質(zhì),從“講清數(shù)學(xué)道理”“加深數(shù)學(xué)理解”“發(fā)展數(shù)學(xué)理性”三個維度與課程標準中的四個方面進行融合,刻畫學(xué)生通過理學(xué)活動所能達成的學(xué)習(xí)效果。與一般的教學(xué)目標相比,理學(xué)目標的確定依據(jù)和語言表述有所不同。
首先,理學(xué)目標必須依據(jù)學(xué)材分析和學(xué)情調(diào)研而定。基于之前所述的“圓的面積”學(xué)材分析和學(xué)情調(diào)研,本節(jié)課的理學(xué)目標見表2。其次,理學(xué)目標的語言表達方式不同。一般教案中,教學(xué)目標的行為主體是教師,語言表述通常采用“使學(xué)生……”的形式,顯然是站在教師的立場和視角來設(shè)定目標,而理學(xué)目標的行為主體是學(xué)生,目標中的數(shù)學(xué)活動需要學(xué)生親力親為,“以生為本”成為必然。
4.理學(xué)歷程
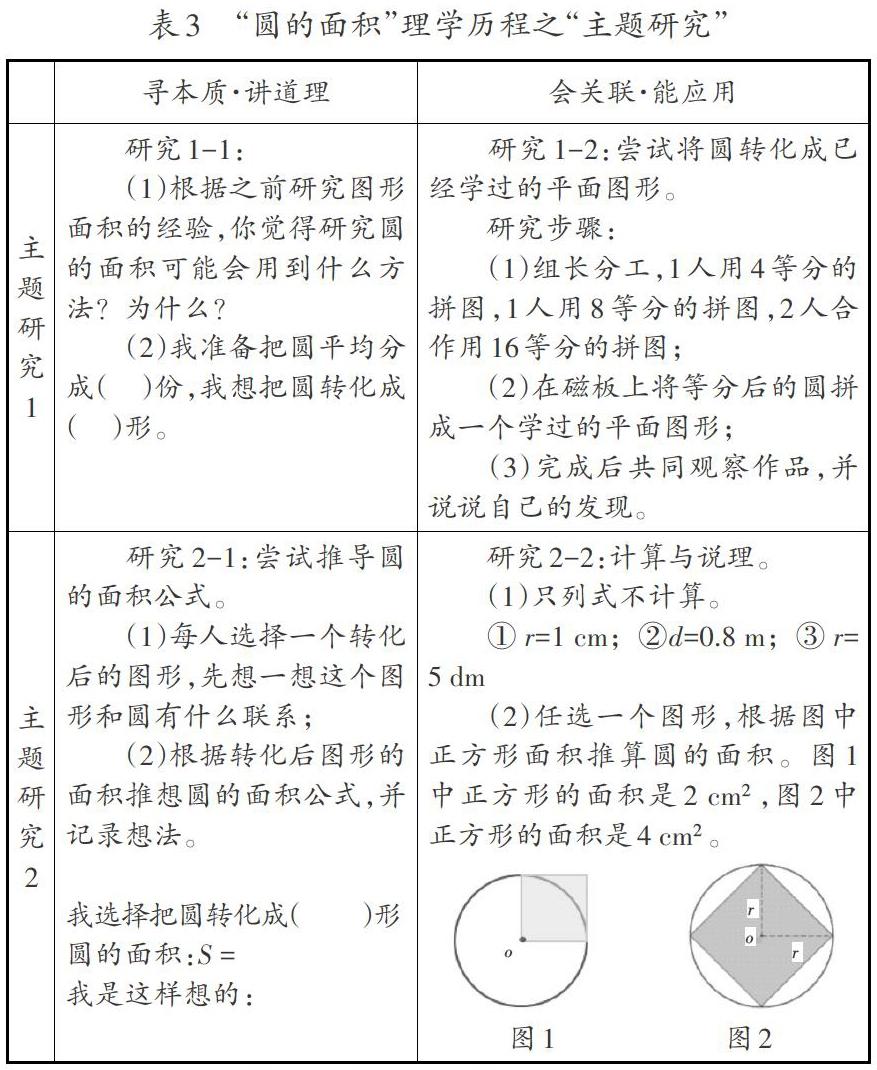
“理學(xué)歷程”是記錄教師“怎么教”、學(xué)生“怎么學(xué)”的檔案,包括“主題研究”和“實施要點”兩個部分。“主題研究”是專供學(xué)生自主研究的學(xué)習(xí)單,它不僅要提供由理學(xué)目標分解、提煉而來的研究任務(wù),而且要準確記錄學(xué)生經(jīng)歷自主學(xué)習(xí)過程中的所思、所想、所為。“實施要點”是對教師如何組織學(xué)生開展主題研究的方法、策略的記錄。因而,“理學(xué)歷程”既是記錄學(xué)生學(xué)習(xí)過程和結(jié)果的評價表,也是留存和傳遞教學(xué)方法的備課手冊。由于“實施要點”是一般教案的主要內(nèi)容,本文略過不談,只結(jié)合表3討論“主題研究”設(shè)計應(yīng)注意的問題。
首先,“理學(xué)歷程”中的主題研究任務(wù)要與理學(xué)目標具有一致性,要以理學(xué)目標為導(dǎo)向,并始終圍繞如何實現(xiàn)理學(xué)目標展開,如表3中“研究1-1” “研究1-2”是為了實現(xiàn)理學(xué)目標“在探索的過程中整體感知平面圖形面積的研究方法,體會‘轉(zhuǎn)化的價值”而設(shè)計的學(xué)習(xí)導(dǎo)入;“研究2-1”不僅指向理學(xué)目標“運用轉(zhuǎn)化策略,探索圓的面積公式”,而且能夠?qū)崿F(xiàn)理學(xué)目標之“能借助操作、觀察、比較、想象、推理等數(shù)學(xué)活動,解釋圓的面積公式由來”;“研究2-2”是對“能進行簡單計算”和“根據(jù)圓的面積公式對圓和以半徑為邊長的正方形面積之間的關(guān)系做適度推想和關(guān)聯(lián)”這兩個理學(xué)目標的落實。
其次,在“理學(xué)歷程”中,學(xué)習(xí)活動要有層次、有梯度,不同的主題研究任務(wù),以及同一主題內(nèi)的新知建構(gòu)任務(wù)和關(guān)聯(lián)運用任務(wù),都必須遵循學(xué)生的認知規(guī)律,循序漸進、螺旋上升。例如表3中的4個主題研究任務(wù)按照“尋找方法”“嘗試轉(zhuǎn)化”“拓展應(yīng)用”的思路由淺入深,層層推進,而在每一個主題研究內(nèi)部,“尋本質(zhì)·講道理”欄目側(cè)重新知的探索、建構(gòu),“會關(guān)聯(lián)·能運用”更關(guān)注知識的關(guān)聯(lián)、運用以及思維是否得到進階。
三、理學(xué)案的編制原則
理學(xué)案編制時要遵循一體化原則、一致性原則、易操作原則。
1.一體化原則
理學(xué)案中的一體化主要是指教案、學(xué)案一體化。當(dāng)下,教師常用的教學(xué)方案有兩種,一種是從如何教的層面進行設(shè)計的傳統(tǒng)教案,包括教學(xué)目標、教學(xué)重難點、教學(xué)過程等,其中教學(xué)過程最為重要,通常含有復(fù)習(xí)引入、教學(xué)新知、鞏固練習(xí)、全課總結(jié)環(huán)節(jié);另一種是導(dǎo)學(xué)案或?qū)W案,從如何引導(dǎo)學(xué)生自主學(xué)習(xí)的層面進行設(shè)計,呈現(xiàn)形式為學(xué)習(xí)單,內(nèi)容多是學(xué)生課上(或課前)需要解決的任務(wù)、習(xí)題等。
崔允漷教授提出的學(xué)歷案是教案、學(xué)案一體化的代表,但其包含要素較多,且適用對象為中學(xué)生。考慮到小學(xué)生開展大單元、大容量主題化學(xué)習(xí)的能力有限,理學(xué)案在學(xué)歷案的基礎(chǔ)上做了適度調(diào)整:(1)將大單元設(shè)計分解成課時學(xué)習(xí);(2)保留學(xué)習(xí)(理學(xué))目標、學(xué)習(xí)過程(理學(xué)歷程)等核心部分,將評價、檢測等內(nèi)容融入學(xué)習(xí)過程(理學(xué)歷程),加大學(xué)情調(diào)研比重;(3)借鑒南京市“小學(xué)數(shù)學(xué)學(xué)歷案”的設(shè)計理念和使用方法,將理學(xué)歷程中的“主題研究”以學(xué)習(xí)單的形式發(fā)給學(xué)生課上使用;(4)為方便教師組織教學(xué)和供他人參考,理學(xué)案中增加“實施要點”欄目,記錄“主題研究”的落實方法和步驟。以上幾點在表4中皆有體現(xiàn)。
2.一致性原則
理學(xué)案編制的一致性原則包括三層含義:一是主題研究任務(wù)與理學(xué)目標的一致性;二是主題研究中“會關(guān)聯(lián)·能應(yīng)用”與“尋本質(zhì)·講道理”的一致性;三是理學(xué)案的設(shè)計理念與“至理數(shù)學(xué)”教學(xué)主張的關(guān)鍵特質(zhì)的一致性。
理學(xué)案是一種基于“標準”的教學(xué),理學(xué)目標需要借助主題研究任務(wù)加以實現(xiàn),因此每一個研究任務(wù)的設(shè)計都來源或指向理學(xué)目標。而在每一個主題研究內(nèi)部,主要通過“尋本質(zhì)·講道理”對新知進行建構(gòu),完成后立刻通過“會關(guān)聯(lián)·能應(yīng)用”對達成情況進行評價。由此可見,理學(xué)案中的所有學(xué)習(xí)過程都是按照理學(xué)目標有序推進,只有一個主題研究任務(wù)完成并且得到了及時的評價,方能進入下一個主題研究。如此設(shè)計也是教、學(xué)、評一致性的充分體現(xiàn)。
“至理數(shù)學(xué)”的關(guān)鍵特質(zhì)是“回歸本質(zhì)”,即數(shù)學(xué)學(xué)習(xí)要堅守學(xué)科本質(zhì)、兒童本位、素養(yǎng)本真。作為教學(xué)主張在課堂落地生根的有效載體,理學(xué)案設(shè)計理應(yīng)處處彰顯“回歸本質(zhì)”。在“圓的面積”理學(xué)案中,對課程標準、教材和其他與之相關(guān)的支持性學(xué)材的分析,對理學(xué)目標中“數(shù)學(xué)道理、數(shù)學(xué)理解、數(shù)學(xué)理性”的挖掘與提煉是對學(xué)科本質(zhì)的堅守;在學(xué)情調(diào)研中,關(guān)注學(xué)生的年齡、心理特點和認知水平,對學(xué)生前測和后測情況進行分析,以及理學(xué)歷程中所有的主題研究都需要學(xué)生主動參與,是“至理數(shù)學(xué)”教學(xué)主張中“兒童本位”的有力佐證。
3.易操作原則
易操作原則是指理學(xué)案設(shè)計要簡約、可行,便于操作。特別是供小學(xué)生課上使用的“理學(xué)歷程”, 字數(shù)不能太多,內(nèi)容不能過細,要抓核心、拎重點。通常,高年級學(xué)生使用的“理學(xué)歷程”篇幅不超過一張A4紙的正反兩面,中低年級以A4紙的一面為宜,不論年級高低,每節(jié)課上的主題研究均不超過3個。每個主題研究中的任務(wù)語言表述要盡可能簡潔、明確、通俗、活潑,杜絕冗長、含糊和抽象。為了便于記錄思考過程和學(xué)習(xí)痕跡,“理學(xué)歷程”要有留白,特別是有寫一寫、畫一畫,或是粘貼作品的環(huán)節(jié),要留足夠的時間和空間。易操作原則在“圓的面積”理學(xué)歷程之“主題研究”中已有鮮明體現(xiàn)(見表3)。
當(dāng)然,小學(xué)數(shù)學(xué)理學(xué)案設(shè)計需要關(guān)注的要素和原則還有很多,本文的闡述顯然不夠全面,尤其是理學(xué)案設(shè)計研究尚處于初始階段,諸如“小學(xué)階段的內(nèi)容都適合用理學(xué)案進行學(xué)習(xí)嗎?”“同課型的理學(xué)案設(shè)計結(jié)構(gòu)一致嗎?”等疑問和困惑還有很多,但我們相信,只要堅守學(xué)科本質(zhì)和兒童本位,數(shù)學(xué)教學(xué)就會向著素養(yǎng)本真回歸。
[ 參 考 文 獻 ]
[1] 張明紅,劉娟娟.回歸本質(zhì):“至理數(shù)學(xué)”教學(xué)主張的內(nèi)涵解讀[J].小學(xué)數(shù)學(xué)教師,2019(10).
[2] 崔允漷.指向深度學(xué)習(xí)的學(xué)歷案[J].人民教育,2017(20).
[3] 劉娟娟.學(xué)歷案:促進課堂中教—學(xué)—評的一致性[J].教學(xué)月刊小學(xué)版(數(shù)學(xué)),2018(Z1).
[4] 中華人民共和國教育部.義務(wù)教育數(shù)學(xué)課程標準(2011年版)[S].北京:北京師范大學(xué)出版社,2012.
【本文系江蘇省中小學(xué)教學(xué)研究第十三期重點自籌課題“以理學(xué)案為載體的‘至理數(shù)學(xué)課例群建設(shè)研究”(課題編號:2019JK13-ZB08)的研究成果。】
(責(zé)編 金 鈴)

