基于單元整合 優(yōu)化數(shù)學(xué)教學(xué)
杜山
[摘 要]在核心素養(yǎng)理念的指引下,實(shí)施小學(xué)數(shù)學(xué)整合化教學(xué)可從根本上改善教學(xué)效果。教師可根據(jù)小學(xué)數(shù)學(xué)教材內(nèi)容的編排特征,橫向整合單元內(nèi)容,縱向重新構(gòu)建課時(shí)內(nèi)容,以多個(gè)角度將單元要素整合到位,從而推動(dòng)學(xué)生進(jìn)行深度學(xué)習(xí)。
[關(guān)鍵詞]單元整合;單元內(nèi)容;課時(shí)內(nèi)容
[中圖分類號(hào)] G623.5[文獻(xiàn)標(biāo)識(shí)碼] A[文章編號(hào)] 1007-9068(2021)08-0041-02
單元教學(xué)整合絕非只是簡(jiǎn)單地整合單元學(xué)習(xí)內(nèi)容,而是以精確掌握學(xué)生的學(xué)習(xí)起點(diǎn)為前提,站在宏觀的立場(chǎng)上歸納單元中的詳細(xì)內(nèi)容,集中單元中的重難點(diǎn),通過拓展、重構(gòu)等策略加工單元知識(shí)點(diǎn),以促進(jìn)學(xué)生進(jìn)行深度學(xué)習(xí)。深度學(xué)習(xí)可促進(jìn)學(xué)生深刻理解知識(shí),幫助學(xué)生完成知識(shí)的遷移,更替學(xué)生的認(rèn)知,使學(xué)生實(shí)現(xiàn)自我內(nèi)化。數(shù)學(xué)教師應(yīng)從宏觀視角把握好知識(shí)之間的內(nèi)在聯(lián)系,從學(xué)生的認(rèn)知起點(diǎn)出發(fā),有效實(shí)施單元整合教學(xué),從而達(dá)到高效化教學(xué)的目的。單元整合教學(xué)要重點(diǎn)做好單元內(nèi)容的重組與課時(shí)內(nèi)容、單元要素的重構(gòu)。
一、單元內(nèi)容——板塊化重組
小學(xué)數(shù)學(xué)教材中,某些單元的內(nèi)容在結(jié)構(gòu)上有一定的共性,教學(xué)時(shí)教師可對(duì)這些單元內(nèi)容進(jìn)行板塊化重組,以促進(jìn)學(xué)生精準(zhǔn)掌握相關(guān)內(nèi)容的共性與聯(lián)系,從而實(shí)現(xiàn)結(jié)構(gòu)化的知識(shí)整合。
例如,乘法口訣是二年級(jí)數(shù)學(xué)教學(xué)的重點(diǎn),與乘法口訣相關(guān)的內(nèi)容有兩個(gè)單元,為了讓學(xué)生更好地掌握乘法口訣,筆者對(duì)這兩個(gè)單元的內(nèi)容進(jìn)行了板塊化重組,分三個(gè)階段引導(dǎo)學(xué)生開展乘法口訣的學(xué)習(xí),學(xué)習(xí)重點(diǎn)指向理解乘法口訣的意義。第一階段,學(xué)習(xí)5的乘法口訣,并進(jìn)行深度理解;第二階段,完成2、3、4的乘法口訣的推導(dǎo);第三段,自主完成6、7、8、9的口訣的學(xué)習(xí)。在學(xué)習(xí)5的乘法口訣時(shí),讓學(xué)生圍繞乘法意義,輔以點(diǎn)子圖進(jìn)行推理;編寫“四五二十”這句口訣,讓學(xué)生試著在5的基礎(chǔ)上進(jìn)行相應(yīng)減少或者增加,繼續(xù)推理,順理成章地完成9句口訣。以點(diǎn)子圖為工具,能夠幫助學(xué)生簡(jiǎn)單地完成5的乘法口訣的推導(dǎo),這一方式對(duì)于其他數(shù)字的乘法口訣的推導(dǎo)也適用,可讓學(xué)生利用豎著增減的方式,或者添加新點(diǎn)子,完成其他數(shù)字的乘法口訣的推導(dǎo)。在口訣教學(xué)中,采用數(shù)形結(jié)合方法,可讓學(xué)生深刻理解“幾個(gè)幾”,精確掌握概念的生成過程。
教師在教學(xué)中提問學(xué)生:“6個(gè)5比5個(gè)5多多少?”大部分學(xué)生都可以直接作答,然而若把文字?jǐn)⑹鲛D(zhuǎn)變?yōu)樗闶健?×6=5×5+( )”時(shí),一部分學(xué)生就會(huì)理解困難。由此可知,即便學(xué)生可以快速記憶乘法口訣,但由于他們并沒有真正理解其中的深層含義,所以無法靈活應(yīng)用。為了化解學(xué)生的理解難點(diǎn),筆者設(shè)計(jì)了兩個(gè)“玩轉(zhuǎn)乘法”的數(shù)學(xué)游戲。
玩法1:算式接龍。讓學(xué)生選擇自己所喜愛的算式,然后寫出相應(yīng)的舉一反三的變式。
玩法2:算式開花。教師給出口訣“四八三十二”,要求學(xué)生回答該口訣可以解決的問題,并在卡片上寫下答案,闡述自己的理解。
學(xué)生的理解五花八門,如“4+4+4+4+4+4+4+4= ” “5×8-8= ” “3×8+8= ” 。還有學(xué)生畫出了許多圖示,比如點(diǎn)子圖、實(shí)物圖等。
上述案例中,教師對(duì)單元內(nèi)容進(jìn)行板塊化重組,引導(dǎo)學(xué)生進(jìn)行統(tǒng)整化學(xué)習(xí),有效提升了學(xué)生的數(shù)學(xué)學(xué)習(xí)效率。
二、課時(shí)內(nèi)容——遞進(jìn)式重構(gòu)
現(xiàn)行的數(shù)學(xué)教材中,大部分內(nèi)容都是以遞進(jìn)的方式呈現(xiàn)的,教師在把握這些內(nèi)容時(shí)既要關(guān)注知識(shí)遞進(jìn)的特點(diǎn),還要注意把握它們之間的邏輯關(guān)系。教學(xué)中,教師可對(duì)相關(guān)課時(shí)內(nèi)容進(jìn)行遞進(jìn)式重構(gòu),使它們形成一個(gè)整體,然后引導(dǎo)學(xué)生整體感知,尋找知識(shí)間的異同點(diǎn),再逐步掌握局部,從而牢固掌握相關(guān)知識(shí)。葉瀾教授曾經(jīng)談到,必須要格外關(guān)注數(shù)學(xué)知識(shí)的研究進(jìn)程,在這之中有兩個(gè)方面最為重要,其一,需要在知識(shí)體系中體現(xiàn)內(nèi)在關(guān)系以及多重關(guān)系,只有這樣,才能夠發(fā)揮出整合效應(yīng);其二,需要表現(xiàn)在學(xué)生的生命活動(dòng)上,關(guān)注其中的內(nèi)在聯(lián)系,注意協(xié)調(diào)發(fā)展。
例如,在教學(xué)“分?jǐn)?shù)”時(shí),為了使學(xué)生深度理解和掌握分?jǐn)?shù)的實(shí)質(zhì),筆者重新建構(gòu)了本課時(shí)的內(nèi)容。正式重構(gòu)前分?jǐn)?shù)部分有5個(gè)課時(shí),重構(gòu)后變?yōu)?個(gè)課時(shí),學(xué)習(xí)重心放在“數(shù)量”和“關(guān)系”兩個(gè)部分上。重構(gòu)后的6個(gè)課時(shí)中,學(xué)生需要精確地掌握分?jǐn)?shù)的含義,具體可分為三個(gè)層級(jí):第一,分?jǐn)?shù)并不僅僅為一個(gè)數(shù);第二,體現(xiàn)出評(píng)分的過程;第三,所代表的關(guān)系為整體以及部分。詳細(xì)環(huán)節(jié)具體如下:
第一步,逐層逐步按照一定的順序不斷推進(jìn)關(guān)于分?jǐn)?shù)意義的理解。
理解1:分?jǐn)?shù)是新的數(shù),可以比較大小,能夠衡量比1小的量,所以介于0與1之間。
理解2:在平均分某個(gè)整體后,能夠獲得n份,可以表示1被n除。
理解3:分?jǐn)?shù)表示部分和整體的聯(lián)系。
在第1課時(shí)需要關(guān)注以下問題:理解分?jǐn)?shù)時(shí)可以介入拆、分等實(shí)踐活動(dòng),即便這些活動(dòng)能夠產(chǎn)生一定的效果,然而卻不可以長(zhǎng)久依賴這些活動(dòng),倘若只是停留在積累活動(dòng)經(jīng)驗(yàn)上,那么學(xué)生并不能夠真實(shí)地感受到分?jǐn)?shù)的含義。根據(jù)經(jīng)驗(yàn)無法了解知識(shí)的深層內(nèi)涵,如果教學(xué)只停留于經(jīng)驗(yàn),也無法進(jìn)一步啟發(fā)學(xué)生的數(shù)學(xué)思維。因此,筆者在教學(xué)“二分之一”時(shí)沒有直接在課上導(dǎo)入一致的動(dòng)手實(shí)踐活動(dòng),因?yàn)閷?duì)學(xué)生來說,把物品分為兩份完全可以依靠于生活經(jīng)驗(yàn),僅需根據(jù)表象操作。對(duì)此,筆者設(shè)計(jì)了第二幅圖(圖略),這幅圖并沒有平均分,以期利用這幅圖使學(xué)生體會(huì)到,倘若沒有平均分,就不能用二分之一表示,但可用其他分?jǐn)?shù)表示。
第二步,構(gòu)建除法與分?jǐn)?shù)的聯(lián)系。
教師在具體的教學(xué)中大多會(huì)創(chuàng)設(shè)平均分的情境(比如切蛋糕、切西瓜等)導(dǎo)入分?jǐn)?shù)以及平均分的概念,然而卻極少有教師以除數(shù)作為切入點(diǎn)。例如,1÷2和1÷3分別等于幾?哪個(gè)數(shù)能夠作為商呢?以這種方式引導(dǎo)學(xué)生思考,會(huì)令學(xué)生產(chǎn)生認(rèn)知沖突,從而產(chǎn)生學(xué)習(xí)的欲望。某些教師認(rèn)為這提升了教學(xué)要求,屬于拔高教學(xué)。由于五年級(jí)過后才會(huì)學(xué)習(xí)除法和分?jǐn)?shù)的關(guān)系,這里需要指出的是,設(shè)計(jì)該環(huán)節(jié)旨在讓除法意義發(fā)揮引入作用,并非介紹和講解二者之間的關(guān)系,除法的實(shí)質(zhì)就是平均分,因此除法才是學(xué)生了解分?jǐn)?shù)的起點(diǎn)。
三、單元要素——多維度重構(gòu)
內(nèi)容補(bǔ)充并非填充過量的內(nèi)容,由于目前教材自身愈發(fā)簡(jiǎn)潔,普遍不耗費(fèi)大量的筆墨表達(dá)知識(shí)點(diǎn)的深層含義,也時(shí)常會(huì)預(yù)留許多空白,需要師生一同挖掘和填充,這種填充不僅可以擴(kuò)充教材的資源內(nèi)涵,還能夠拓寬學(xué)生思路,更能夠培養(yǎng)學(xué)生的數(shù)學(xué)思維。
例如,在學(xué)生初步把握取近似數(shù)的方法后,教材中重點(diǎn)談到,不可以抹掉小數(shù)末尾的零,通常情況下,教師都會(huì)直接告訴學(xué)生,由于這個(gè)末尾的零表達(dá)精準(zhǔn)度,所以不可以直接抹掉。比如,近似數(shù)0.984,保留一位小數(shù)為1.0,而寫1就是錯(cuò)誤的,這兩者對(duì)比起來1.0更精確,然而此種表述和講解卻可能令學(xué)生在理解上產(chǎn)生困擾,數(shù)字同樣大,說1.0更為精確的原因是什么呢?這也成為本課的教學(xué)難點(diǎn)。
因此,筆者在教學(xué)時(shí),先變式例題,接著補(bǔ)充:某運(yùn)動(dòng)員的身高為1.862米。下面對(duì)其身高的小數(shù)做保留整數(shù)一位、兩位小數(shù)處理,然后提問:“大家認(rèn)為目前哪個(gè)答案和之前的最契合?”學(xué)生把得到的三個(gè)數(shù)字同原數(shù)字比較,最后計(jì)算所得的差值分別為0.138米、0.038米和0.002米。這樣便可以更加直接地體會(huì)到保留兩位小數(shù)和原來的數(shù)值差距最小,把握好精準(zhǔn)度的含義。
在講解上述例題后,筆者展開了如下補(bǔ)充。
(1)理解題意,提煉方法
教師提問:“某個(gè)同學(xué)在將其身高的數(shù)值精確至十分位以及百分位后分別為1.5米和1.50米,他的真實(shí)身高可能為多少呢?”引導(dǎo)學(xué)生先了解題意,接著依托“( )≈1.5”進(jìn)行反向推理。
(2)學(xué)生嘗試,反饋答案
學(xué)生得出:“為了能夠滿足條件‘( )≈1.5,該數(shù)字所在區(qū)間應(yīng)當(dāng)為1.45~1.54;為了滿足‘( )≈1.50,該數(shù)字所在的區(qū)間可能為1.495~1.50。”
(3)數(shù)形結(jié)合,促進(jìn)理解
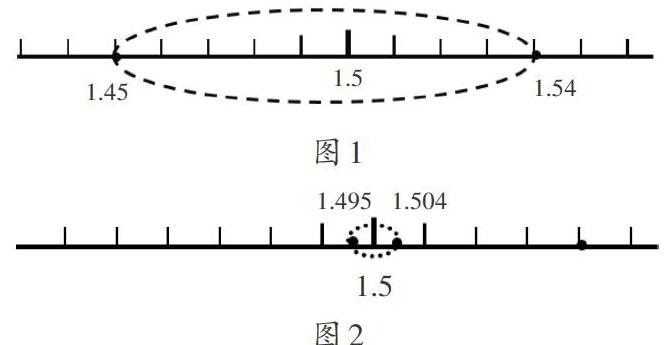
聯(lián)系學(xué)生的回答,為學(xué)生導(dǎo)入數(shù)軸,以其來表示1.5和1.50的取值范圍(如圖1和圖2所示),這里需要特別注意,由于這種表示方法為學(xué)生自己所推導(dǎo),若嚴(yán)謹(jǐn)分析,會(huì)發(fā)現(xiàn)有一定的缺陷。對(duì)比兩個(gè)圖能夠發(fā)現(xiàn),1.50的取值范圍相較1.5更小,因此代表著末位的0不可以抹掉,否則精準(zhǔn)度也會(huì)隨之變動(dòng)。
總之,大部分教師在數(shù)學(xué)教學(xué)中都會(huì)按照教材的編排順序進(jìn)行教學(xué),而沒有以整體的視角分析教學(xué)內(nèi)容。而單元整合教學(xué)則有效把握了教學(xué)本質(zhì)以及教學(xué)重點(diǎn),在應(yīng)用教材中體現(xiàn)出了教師的創(chuàng)造力。對(duì)于每位教師來說,這種教學(xué)方式離不開不斷努力、反復(fù)嘗試與深度探索。因此,教師應(yīng)當(dāng)站在宏觀的立場(chǎng)上,虛心接受學(xué)生給出的建議,以靈活的方式重組和整合教學(xué),只有這樣,才能夠助推教育觀念的轉(zhuǎn)換,促進(jìn)學(xué)生個(gè)人素養(yǎng)的提高,實(shí)現(xiàn)讓學(xué)生深度學(xué)習(xí)的目標(biāo)。
[[ 參 考 文 獻(xiàn) ]]
[1] 林崇德.學(xué)習(xí)與發(fā)展:中小學(xué)生心理能力發(fā)展與培養(yǎng)[M].北京:北京師范大學(xué)出版社,1991.
[2] 鄭毓信.數(shù)學(xué)思維與小學(xué)數(shù)學(xué)[M].南京:江蘇教育出版社,2008.
[3] 曾江麗.對(duì)小學(xué)數(shù)學(xué)教學(xué)重組的幾點(diǎn)思考[J].中小學(xué)教學(xué)研究,2012(5).
(責(zé)編 黃春香)

