在一題多解中培養思維的靈活性
江蘇省泰州實驗學校 高明月
思維品質是人的思維的個性特征。思維品質反映了每個個體智力或思維水平的差異,主要包括深刻性、靈活性、獨創性、批判性、敏捷性和系統性六個方面。思維的靈活性是建立在思維的系統性和深刻性的基礎上,并為思維的敏捷性、獨創性和批判性提供保證。因此,培養思維的靈活性顯得尤為重要。
一題多解是指從不同的角度,運用不同的思維方式來解答同一道題的思考方法。一題多解是小學數學教學中常用的方法,被認為是提高學生解題能力、培養學生思維靈活性的有效方法。經常進行一題多解的訓練,可以鍛煉學生的思維,使學生的頭腦更靈活。
下面結合兩個案例談談如何在一題多解中培養學生思維的靈活性。
一、分數除法應用題
問題1:行駛1 千米用汽油多少升?
問題2:1 升汽油可以行駛多少千米?
這道分數除法應用題是蘇教版六年級上冊“分數除法”單元的習題,學生的困惑是弄不清誰除以誰,經常把被除數和除數寫反了。針對這一情況,一題多解的訓練不僅可以拓寬學生的解題思路,溝通知識間的內在聯系,而且能有效地幫助學生突破難點,培養學生思維的靈活性。
方法一:畫圖法
借助圖形化抽象為具體,弄清數量之間的關系,促進數學理解。
問題1:行駛1 千米用汽油多少升?
(1)畫圖。把題目中的條件和問題整理在線段圖上,如圖1:
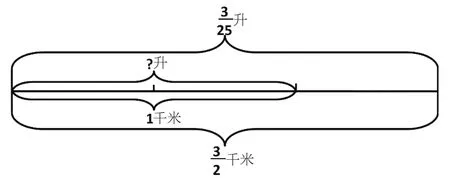
圖1


(3)出示數量關系式:總數÷份數=每份數。
問題2:1 升汽油可以行駛多少千米?
(1)畫圖。把第一個問題的答案作為已知條件整理在線段圖上,如圖2:
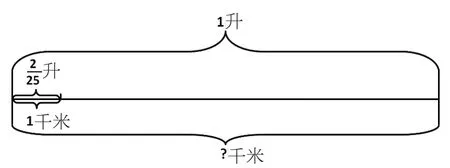
圖2
(3)出示數量關系式:總數÷每份數=份數。
方法二:倍比法
解應用題時,先求出題中兩個對應的同類數量的倍數,再通過倍數去求未知數,這種解題的方法稱為倍比法。
問題1:行駛1 千米用汽油多少升?
(1)先把條件和問題整理一下。
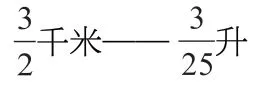
1 千米 ——?升

問題2:1 升汽油可以行駛多少千米?
(1)整理一下條件和問題:

?千米 —— 1 升

方法三:遷移法
把整數除法的意義遷移到分數除法中來。
把題目中的分數換成整數,就成了這樣一道題:“一輛小汽車行駛1000 千米用汽油80 升。問題1:行駛1 千米用汽油多少升?問題2:1 升汽油可以行駛多少千米?”
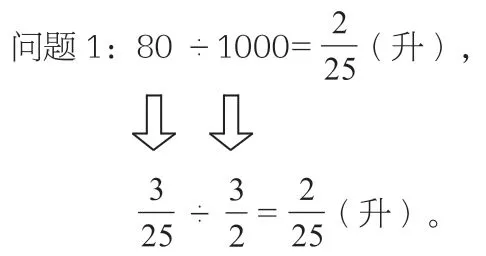
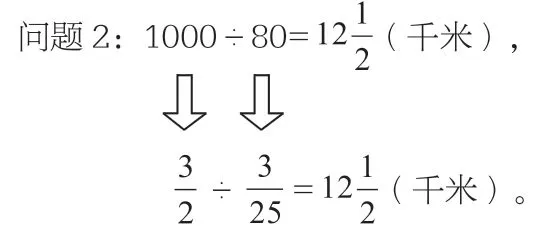
畫圖法借助直觀的圖形,有助于弄清數量之間的關系。倍比法把兩個同類量進行倍比,可以將紛繁的關系變得簡潔明了。遷移法將新知轉化為舊知,借助已有的知識經驗來解決新問題。通過一題多解的訓練,學生能從不同的角度,運用不同的思維方式來思考問題,在思維過程中能從一種解題途徑轉向另一種解題途徑,能舉一反三、觸類旁通,從而培養學生思維的靈活性。
二、移多補少應用題
【例2】小明和小紅各有一些糖,小明給小紅3 顆糖以后,小明還比小紅多2 顆糖,原來小明比小紅多多少顆糖?
這道移多補少應用題是一年級的數學思維訓練題。在課前的調查中,多數學生認為原來小明比小紅多5 顆糖,錯誤率較高。一年級學生抽象思維的水平較低,畫圖法變抽象為具體,再結合詳細的講解,會促進學生的理解。
方法一:畫圖法和倒推法的融合
(1)指導畫圖。
從后來的情況想起。后來,“小明比小紅多2 顆糖”,他們兩人一樣多的糖有多少呢?我們不知道,也不需要知道,用省略號表示小明有這么多糖,小紅也有這么多糖,這是他們兩人一樣多的部分,如圖3:

圖3
“小明給了小紅 3 顆糖以后,小明還比小紅多2 顆糖”,說明這3 顆糖小明也有。小紅的3 顆糖是小明給她的,要還給小明,原來小明比小紅多8 顆糖。3+2+3=8(顆)。(如圖4)
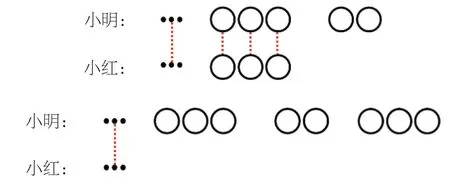
圖4
(2)了解“倒推法”。
后來,“小明比小紅多2 顆糖”,原來,小明比小紅多8 顆糖。由后來的情況去推想原來的情況,這種方法叫作“倒推法”。(如圖5)
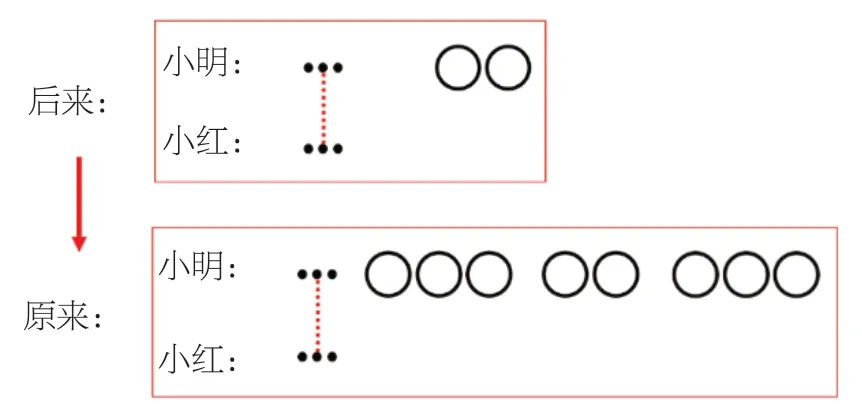
圖5
方法二:畫圖法、假設法和倒推法的融合
(1)從后來的情況想起,假設小紅后來有5 顆糖,那么小明后來有7 顆糖,小紅的3 顆糖是小明給她的,要還給小明,原來小明有10 顆糖,小紅有2 顆糖,原來小明比小紅多8 顆糖。5-3=2(顆), 7+3=10(顆),10-2=8(顆)。
(2)課件演示。(如圖6)
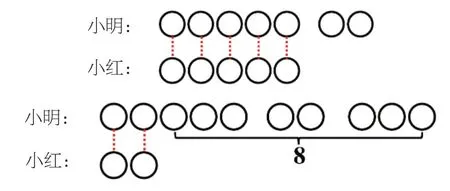
圖6
(3)追問:“能不能假設小紅后來有2 顆糖呢?”(小明給了小紅3 顆糖,小紅要還給小明3 顆糖,如果假設小紅有2 顆糖,不夠還給小明)看來,假設的糖的顆數要夠還給別人才行。
在解決問題時,引導學生從后來的情況想起,找到解決問題的突破口,接著指導畫圖、課件演示,既降低了學生思考的負荷,又讓學生體會到倒推法的巨大作用。假設法是先假想出一種結果,再推想出原來兩人相差的糖的顆數。
倒推法與假設法的有機融合,使學生體會到解決問題策略的多樣性,又培養了思維的靈活性。思維的靈活性體現在:思維起點靈活,從不同角度、方向,用多種方法來解決問題;思維過程靈活,從分析到綜合,從綜合到分析,全面而深刻地思考問題。多種策略的呈現打開了學生的思路,培養學生從不同角度思考問題的習慣,進而較全面地分析問題、解決問題,再用同類問題加以鞏固練習,學生在方法的遷移中,逐步達到舉一反三、運用自如的程度,從而提升思維的品質。
學生思維品質的提升是一個漫長的過程,不是一朝一夕就能實現的,只有用心栽培,方能靜待花開。

