如何提升學(xué)生的表達(dá)能力

王孝勤 李芳芳

[摘 要]表達(dá)能力作為一種基本素養(yǎng)，不僅可以加深學(xué)生對(duì)知識(shí)的理解，更能幫助學(xué)生深入學(xué)習(xí)，而且對(duì)于學(xué)生的人際交往和未來(lái)發(fā)展都有著深遠(yuǎn)的影響。小學(xué)階段是培養(yǎng)學(xué)生表達(dá)能力的重要時(shí)期，表達(dá)能力的培養(yǎng)不應(yīng)局限于課堂，而應(yīng)貫穿于學(xué)習(xí)活動(dòng)的始終。如何在數(shù)學(xué)教學(xué)中提升學(xué)生的表達(dá)能力，使學(xué)生想表達(dá)、敢表達(dá)、會(huì)表達(dá)，并做到言之有物、言之有理、言之有序、言之有力，是教育工作者要重點(diǎn)關(guān)注的問(wèn)題。

[關(guān)鍵詞]言之有物;言之有理;言之有序;言之有力;表達(dá)能力

[中圖分類號(hào)] G623.5[文獻(xiàn)標(biāo)識(shí)碼] A[文章編號(hào)] 1007-9068（2021）11-0076-02

兒童時(shí)期是培養(yǎng)一個(gè)人表達(dá)能力的最佳時(shí)期，如果能在這一時(shí)期對(duì)學(xué)生的表達(dá)能力進(jìn)行一定的培養(yǎng)和訓(xùn)練，讓學(xué)生的表達(dá)有內(nèi)容、有邏輯、有順序、有感染力和說(shuō)服力，那么學(xué)生未來(lái)的表達(dá)能力必定會(huì)非常高。

在課堂上，學(xué)生在表達(dá)時(shí)經(jīng)常會(huì)出現(xiàn)無(wú)話、無(wú)條理以及無(wú)說(shuō)服力的情況，面對(duì)這些情況，教師應(yīng)該怎么做呢？

一、讓學(xué)生從言之無(wú)物到言之有物

1.前置問(wèn)題，改變學(xué)習(xí)順序

課堂上經(jīng)常會(huì)出現(xiàn)教師提出問(wèn)題后，沒(méi)有學(xué)生舉手回答的現(xiàn)象，是因?yàn)閷W(xué)生不知道該怎么回答，還是學(xué)生根本就不會(huì)？反觀課下，學(xué)生總是滔滔不絕說(shuō)個(gè)不停。我想，課堂上學(xué)生沉默可能是因?yàn)樗麄儾恢勒f(shuō)什么，更不知道怎樣去表達(dá)。如果我們能把問(wèn)題放在課前，給學(xué)生充足的時(shí)間進(jìn)行思考和交流，等到了課堂上，學(xué)生的表達(dá)必定是深刻的，也必定會(huì)言之有物。

例如，在教學(xué)“兩位數(shù)乘兩位數(shù)”前，我發(fā)給學(xué)生一張“預(yù)習(xí)單”，讓學(xué)生帶著問(wèn)題去預(yù)習(xí)。

通過(guò)課前發(fā)“預(yù)習(xí)單”的方式，使得學(xué)生有充足的時(shí)間進(jìn)行思考，并把自己的想法記錄下來(lái)。學(xué)生用三種方法計(jì)算出14×12的結(jié)果。第一種是用點(diǎn)子圖先算14×10=140，再算14×2=28，最后把兩個(gè)乘積相加140+28=168。第二種是畫(huà)長(zhǎng)方形，學(xué)生通過(guò)圖形看出要求14×12的結(jié)果就是求這個(gè)長(zhǎng)方形的面積，然后把這個(gè)長(zhǎng)方形分成兩個(gè)小長(zhǎng)方形，分別求出小長(zhǎng)方形的面積再相加，算出14×12=168。第三種是把12變成3×4，也就是把算式14×12變成14×3×4，先算14×3=42，再算42×4=168。課前預(yù)習(xí)給了學(xué)生充足的時(shí)間思考，當(dāng)學(xué)生思考出多種算法并能很好地理解算法時(shí)，在課堂上的表現(xiàn)必然是積極的，表達(dá)必然是言之有物的。

2.開(kāi)放問(wèn)題，優(yōu)化學(xué)習(xí)支架

常規(guī)的提問(wèn)方式一般是教師問(wèn)一句學(xué)生答一句，并不能很好地鍛煉學(xué)生的表達(dá)能力，學(xué)生的回答也是言之無(wú)物的。如果教師換一種方式提問(wèn)，使問(wèn)題更具開(kāi)放性，給學(xué)生更多思考的機(jī)會(huì)，我相信學(xué)生的表達(dá)能力必然會(huì)有所提升。

例如，在教學(xué)“認(rèn)識(shí)小數(shù)”時(shí)，學(xué)生按部就班地完成教師布置的任務(wù)：先尋找生活中的小數(shù)，再說(shuō)一說(shuō)什么是小數(shù)，比較小數(shù)和分?jǐn)?shù)的聯(lián)系和區(qū)別，這并沒(méi)有給學(xué)生自主思考的空間。但如果讓學(xué)生用不同的方法表達(dá)0.3這個(gè)小數(shù)，學(xué)生可能會(huì)有幾種不同的表達(dá)方法。

方法1：把一個(gè)長(zhǎng)方形平均分成10份，涂上其中的3份就是0.3。

方法2：把一條線段平均分成10份，其中的3份就可以用0.3表示。

方法3：把面積是1平方分米的正方形平均分成100份，每一份就是1平方厘米，其中的30份可以表示0.3。

通過(guò)畫(huà)一畫(huà)、說(shuō)一說(shuō)，學(xué)生對(duì)分?jǐn)?shù)的理解越來(lái)越深刻，表達(dá)也必然是言之有物的。

二、讓學(xué)生從言之無(wú)理到言之有理

數(shù)學(xué)既是一門講道理的學(xué)科，又是一門有邏輯的學(xué)科，數(shù)學(xué)中的所有結(jié)論都不是憑空而來(lái)的，而是通過(guò)推理、抽象、概括等方式推導(dǎo)來(lái)的，那么，學(xué)生表達(dá)時(shí)怎樣才能做到言之有理呢？

1.理解算法，說(shuō)清算理

有些學(xué)生計(jì)算能力很強(qiáng)，卻不知道為什么這樣算，因?yàn)檫@些學(xué)生對(duì)算法掌握得很熟練，卻不理解算理，這就使得他們?cè)谥v述計(jì)算過(guò)程時(shí)只能說(shuō)出計(jì)算的方法，卻說(shuō)不出算理。

如果教師在教學(xué)中加強(qiáng)算理相關(guān)的訓(xùn)練，多問(wèn)一些“為什么”，學(xué)生的表達(dá)定能從言之無(wú)理變成言之有理。

例如，在教學(xué)“兩位數(shù)乘兩位數(shù)”時(shí)，教師要引導(dǎo)學(xué)生多說(shuō)說(shuō)14×12的算理，讓學(xué)生知道28表示2個(gè)一乘14是28個(gè)一，140表示14乘1個(gè)十是14個(gè)十，14的4應(yīng)該寫(xiě)在十位上，1應(yīng)該寫(xiě)在百位上。

學(xué)生通過(guò)說(shuō)一說(shuō)、練一練加深了對(duì)算理的理解，做到不光“知其然”還“知其所以然”，在表達(dá)時(shí)更能言之有理。

2.結(jié)合數(shù)學(xué)現(xiàn)象說(shuō)清原理

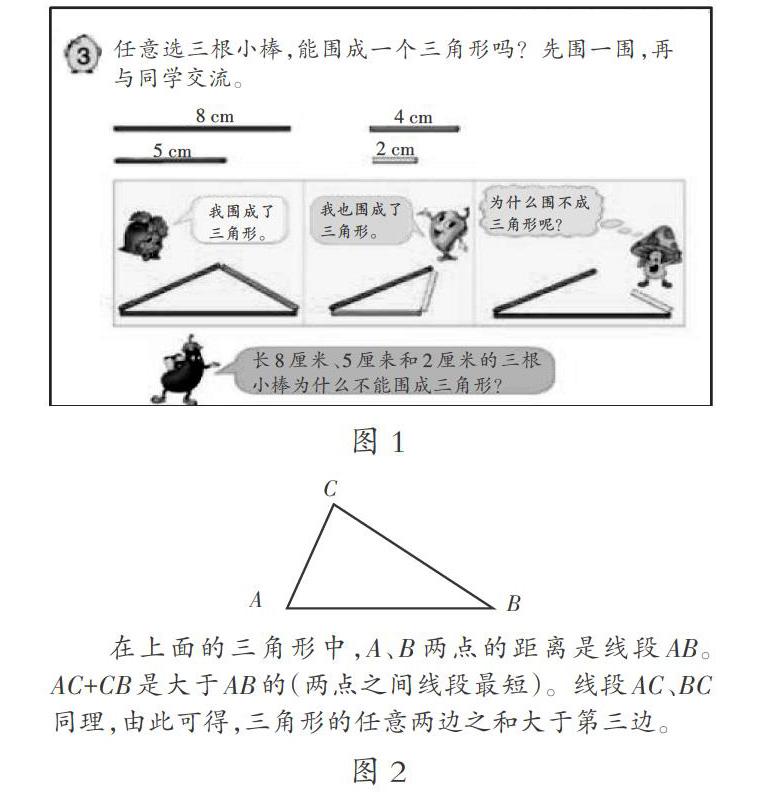
在解釋“三角形的兩邊之和大于第三邊”時(shí)，課本中運(yùn)用了不完全歸納法推出結(jié)論：三角形任意兩條邊長(zhǎng)度的和大于第三邊長(zhǎng)度（如圖1所示）。但是學(xué)生對(duì)此并不能信服。為了讓學(xué)生更清楚背后的原理，我畫(huà)出一個(gè)三角形ABC（如圖2所示），并透過(guò)圖示的數(shù)學(xué)現(xiàn)象幫助學(xué)生說(shuō)清算理。

三、讓學(xué)生從言之無(wú)序到言之有序

有條理的語(yǔ)言可以讓人更清晰地表達(dá)出自己的觀點(diǎn)和想法，讓別人更容易理解。學(xué)生在剛開(kāi)始表達(dá)自己的觀點(diǎn)時(shí)可能有很多話要說(shuō)，但是并不知道該如何有條理地表達(dá)出來(lái)，別人聽(tīng)后仍然會(huì)感覺(jué)很困惑，這樣的表達(dá)是言之無(wú)序的。

如果教師能夠教給學(xué)生一些表達(dá)結(jié)構(gòu)，學(xué)生就可以清楚、有序地表達(dá)自己的觀點(diǎn)。比如告訴學(xué)生可以按照結(jié)構(gòu)順序，用“第一……第二……第三……”等詞連接，或者按照時(shí)間順序，用“先……再……然后……”等詞連接，還可以按照程度順序，用“首先……其次……再次……”等詞連接，等等。

例如，在教學(xué)“長(zhǎng)方形和正方形周長(zhǎng)”時(shí)有這樣一道題：

劉奶奶打算用籬笆圍出一塊長(zhǎng)方形菜地，菜地長(zhǎng)14米、寬12米，一側(cè)靠墻，最少需要多長(zhǎng)的籬笆？

一開(kāi)始學(xué)生的表達(dá)是這樣的：由題可知菜地的形狀是長(zhǎng)方形，長(zhǎng)方形的長(zhǎng)是14米，寬是12米，所以這個(gè)長(zhǎng)方形可能是12米的那條邊靠墻，這樣籬笆的長(zhǎng)就是其他三條邊的長(zhǎng)加起來(lái)，籬笆的長(zhǎng)是14+12+14=40（米），因?yàn)殚L(zhǎng)方形的長(zhǎng)是14米，寬是12米，有一邊靠墻，所以籬笆的長(zhǎng)不是這個(gè)長(zhǎng)方形的周長(zhǎng)，也就不能用（14+12）×2來(lái)算，要減掉一條邊，我們上面用的是12米的邊靠墻，還可以用14米的邊靠墻，如果是14米的邊靠墻，籬笆的長(zhǎng)就是14+12+12=38（米）。又因?yàn)轭}目中讓我們求的是籬笆最少是多長(zhǎng)，所以通過(guò)上面的計(jì)算得籬笆最少是38米。

隨后我讓其他學(xué)生分析這位學(xué)生的表述，大部分學(xué)生表示沒(méi)有聽(tīng)明白。于是我又讓該學(xué)生使用“第一……第二……第三……”這樣的詞，并重新組織語(yǔ)言進(jìn)行講解，下面是該學(xué)生整理后的回答。

我認(rèn)為這道題目應(yīng)該從以下三方面解決：第一，這塊長(zhǎng)方形菜地有兩種圍法，分別是長(zhǎng)方形菜地的一條長(zhǎng)邊靠墻或一條寬邊靠墻;第二，如果是一條長(zhǎng)邊靠墻，那么籬笆的長(zhǎng)就是14+12+12=38（米），如果是一條寬邊靠墻，那么籬笆的長(zhǎng)就是14+14+12=40（米）;第三，題目中要求的是“籬笆最少多長(zhǎng)”，那么答案應(yīng)該是14+12+12=38（米）。

通過(guò)對(duì)比我們不難發(fā)現(xiàn)，把想說(shuō)的話分成一、二、三點(diǎn)，會(huì)使表達(dá)更有序，別人就會(huì)更容易理解。

四、讓學(xué)生從言之無(wú)力到言之有力

沒(méi)有行動(dòng)的語(yǔ)言是蒼白的，只有借助一定的工具才會(huì)使語(yǔ)言更有說(shuō)服力。教師在課堂上要經(jīng)常使用舉例、畫(huà)圖等方式來(lái)增加說(shuō)服力，并讓學(xué)生進(jìn)行模仿。

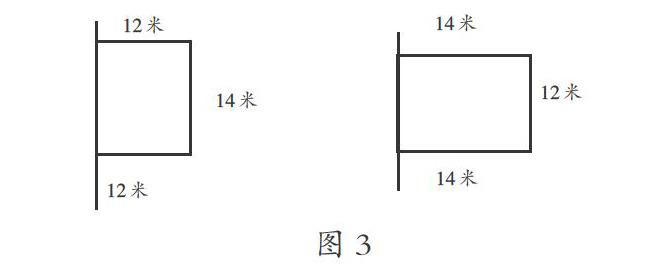
如前文這道題，當(dāng)用畫(huà)圖的方式進(jìn)行講解時(shí)，學(xué)生就非常容易理解（如圖3所示）。

通過(guò)圖示可以清楚地看到：想要一側(cè)靠墻圍出一塊長(zhǎng)14米、寬12米的長(zhǎng)方形菜地，有兩種方法，一種是長(zhǎng)方形的一條長(zhǎng)靠墻，一種是長(zhǎng)方形的一條寬靠墻，顯然當(dāng)長(zhǎng)方形的長(zhǎng)靠墻時(shí)所需的籬笆最少，因此最少需要籬笆14+12+12=38（米）。

舉例也是經(jīng)常使用到的教學(xué)方式，如在教學(xué)“乘法分配律”時(shí)，可以讓學(xué)生用舉例子的方法來(lái)驗(yàn)證（a+b）×c = a×c+b×c的正確性。判斷“兩位數(shù)乘兩位數(shù)的積一定是四位數(shù)”是否正確時(shí)，可以舉例10×11的積是一個(gè)三位數(shù)，從而判斷出此題是錯(cuò)誤的，再讓學(xué)生舉其他例子。通過(guò)舉例可以使定理更具有說(shuō)服力，從而使個(gè)人的表達(dá)從言之無(wú)力到言之有力。

數(shù)學(xué)課中的表達(dá)是一種思維的外在表現(xiàn)，提高學(xué)生的表達(dá)能力是一項(xiàng)細(xì)致的工程，在教學(xué)實(shí)踐中，教師要不斷摸索探究，并實(shí)施更多行之有效的訓(xùn)練方法和手段，帶動(dòng)學(xué)生表達(dá)，讓學(xué)生有話可說(shuō)、有理可依。教師在平時(shí)的教學(xué)中要抓住每個(gè)契機(jī)，讓學(xué)生每天改變一點(diǎn)點(diǎn)，長(zhǎng)久的堅(jiān)持定會(huì)提升學(xué)生的表達(dá)能力。

（責(zé)編 黃 露）