發展數學思維 培養空間觀念

常秀萍

[摘 要]培養學生空間思維和空間觀念是小學數學的重要教學任務之一。以 “圓柱的表面積”教學為例，論述在數學課堂如何激活學生的空間觀念，發展學生的空間觀念，強化學生的空間觀念。

[關鍵詞]圓柱;表面積;空間觀念

[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068（2021）11-0072-02

培養學生的空間思維和空間觀念是小學數學的重要教學任務之一。在教學中，教師應合理利用各種教學手段，從學生的認知水平出發，把抽象的幾何圖形與現實生活中的事物聯系起來，從而有效化解幾何圖像的抽象性，助力學生更快、更好地建構空間觀念。下面以 “圓柱的表面積”教學為例，論述培養學生空間觀念的策略。

一、把握知識聯系，激活空間觀念

學生在學習新知之前已經具備了一定的認知經驗和知識基礎。教師要注重把握新舊知識的聯系，在講授新知之前復習舊知，喚醒學生已有的空間觀念：一是要從學生已有的舊知中尋找切入點，這樣不但能溫故知新，還能激活學生已有的空間觀念;二是借助生活中的感性材料，使學生初步建立圖形表象，激活學生的空間觀念。

【教學片段1】

師：我們已經學過了長方體的表面積。請拿出長方體學具，說說長方體的表面積指的是什么？

生1：長方體有6個面，它的表面積指的是把這6個面的面積加起來。

師：長方體的6個面有什么特點？

生2：長方體的6個面都是平平的，而且都是長方形。

生3：也有可能有兩個正方形。

師：拿出圓柱學具，說說圓柱的表面積指的是什么。

生4：圓柱的表面積指的是兩個底面的面積加上側面的面積。

師：圓柱的表面有什么特點？

生5：上下兩個底面都是平平的圓形，但側面不是一個平面圖形，而是一個曲面。

師：如果要制作一個圓柱形紙盒，接口處不計，至少需要多大面積的紙板呢？

生6：這就是求圓柱的表面積。

生7：它的底面是個圓形，面積很容易就能求出來，可是它的側面怎么求呢？

生8：求圓的面積時，是把圓轉化成長方形。現在或許也可以把圓柱的側面轉化成我們學過的圖形。

師：那讓我們一起來探究圓柱的表面積公式吧！

教師首先引導學生復習長方體表面積的相關知識，激活了學生已有的空間觀念，為進一步探究圓柱的表面積奠定了知識基礎;接著通過看一看、摸一摸、說一說的數學活動，使學生更好地理解了圓柱的表面積的含義，初步建立起圓柱的空間表象;最后，創設情境，激發學生的認知沖突。在“制作圓柱”的情境中，學生利用“舊知”無法解決新的問題，學生達到了“ 心求通而未達 ，口欲言而未能”的“ 憤悱”狀態 ，從而產生了探求新知的強烈欲望。

二、引導數學操作，發展空間觀念

在數學教學中，教師應該指導學生進行實踐操作，促使學生建構幾何概念，發展空間觀念，具體可從以下三個方面入手，一是在操作中觀察;二是在操作中思考;三是在操作中想象。

【教學片段2】

師：我們通過討論得知，圓柱的表面積等于圓柱的側面積加上底面積的2倍。

生1：圓柱的底面積很好計算，問題是圓柱的側面是個曲面，不容易計算。

師：是不是可以嘗試把圓柱的側面轉化成我們學過的圖形呢？

生2：對，我們以前經常用轉化的方法解決問題。

師：請拿出一張長方形的紙，把它卷起來，你有什么發現？

生3：可以卷成一個圓柱。

師：如果沿著它的側面剪開呢？

師：請拿出圓柱學具，以小組為單位進行操作，看看會有什么發現。

（學生操作，教師指導）

師：圓柱的側面轉化成了什么圖形？是如何轉化的？

生4：剪開后展開，得到一個長方形。

師：長方形與圓柱的側面有什么關系呢？

生5：它們的面積是相等的。因為只是形狀發生了變化，并沒有增大或者減小。長方形的長就是圓柱的底面周長，長方形的寬就是圓柱的高。

師：那如何求出圓柱的側面積呢？

生6：圓柱的側面積=長方形面積=長×寬=Ch=2πrh。圓柱的表面積=側面積+底面積×2=2πrh+2πr2。（如圖1）

師：對，圓柱的側面是個曲面，我們把它轉化成長方形，就可以直接求出它的面積了。

生7：我們組有新的發現。我們不小心剪“偏”了，卻意外地發現，圓柱的側面變成了一個平行四邊形。（如圖2）

師：平行四邊形與圓柱的側面之間有什么關系呢？

生8：圓柱的側面積=平行四邊形面積=底×高=Ch=2πrh。圓柱的表面積=側面積+底面積×2=2πrh+2πr2。

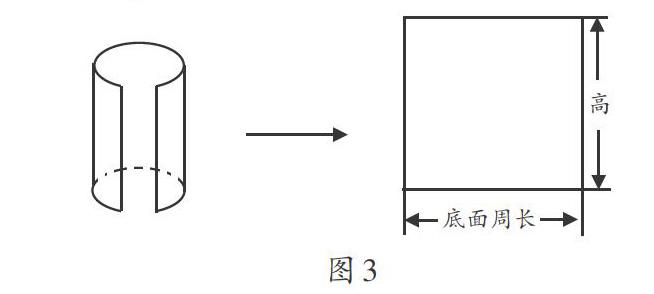
生9：我們剪開后得到了一個正方形（如圖3）。正方形的一條邊長等于圓柱的底面周長，另一條邊長等于圓柱的高。因此，圓柱的側面積=正方形面積=邊長×邊長=Ch=2πrh。圓柱的表面積=側面積+底面積×2=2πrh+2πr2。

師：想一想，什么情況下圓柱的側面展開才是一個正方形呢？

生10：圓柱的底面周長等于圓柱的高時，圓柱側面展開圖是一個正方形。

師：條條大道通羅馬。無論圓柱的側面展開是長方形、平行四邊形，還是正方形，都能得出圓柱的表面積=側面積+底面積×2=2πrh+2πr2。

通過數學操作，學生逐步發展了空間觀念：一是在圖形轉化中發展空間觀念。求圓柱的表面積的關鍵點在于求圓柱的側面積，學生在操作中雖然將圓柱的側面分別轉化成了長方形、平行四邊形和正方形，但是殊途同歸般地得出了相同的結論。教師引導學生分析新圖形與原圖形之間的關系，使學生體驗到了圖形轉化的奧妙以及“化曲為直”的魅力;二是“做”與“思”相結合。在操作的過程中，教師始終以問題 “轉化成什么？”“如何轉化？”“新圖形與原圖形之間有什么關系？” 引領學生，賦予數學操作更深刻的思維意蘊，從而在發展學生數學思維的基礎上，發展了學生的空間觀念。

三、實現思維創新，強化空間觀念

“創新是一個民族進步的靈魂，是一個國家興旺發達的不竭動力。”發展學生的創新思維，既是數學教學的重要任務，也是學生未來發展的需求。在數學教學中，學生通過質疑、探究、操作等方式，可充分發揮想象力，創造性地把立體圖形轉化成平面圖形，在解決問題的過程中實現思維創新，強化空間觀念。

【教學片段3】

生1：盡管我們得出了圓柱的表面積公式，但是這樣的公式看起來并不簡單，計算起來也很麻煩。

師：有更好的辦法讓計算公式變得簡單嗎？

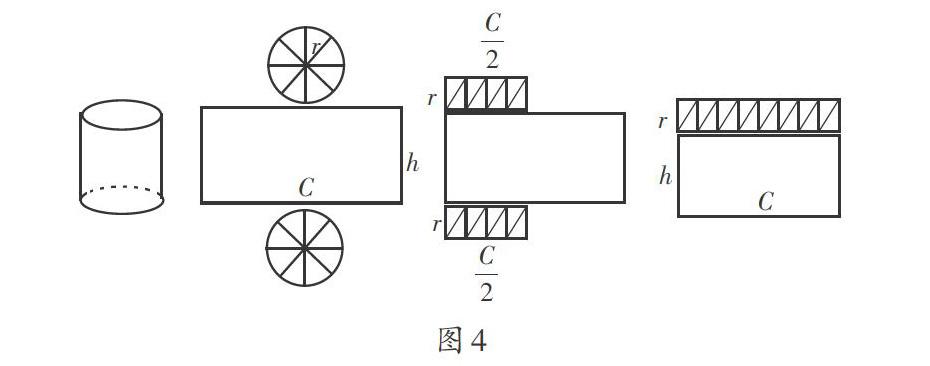
生2：可以借鑒圓形轉化成長方形的經驗，把圓柱的兩個底面也轉化成長方形，合并在圓柱的側面轉化成的長方形中，從而得到一個大長方形，只要求出這個大長方形的面積，就可以求出圓柱的表面積了。如圖4，大長方形的長就是圓柱的底面周長C，高就是（h+r），圓柱的表面積S=C（h+r）。

生3：把整個圓柱的表面變成了一個長方形，這個辦法真奇妙呀。

利用常規的圖形轉化得出圓柱的表面積計算公式后，不少教師就會認為教學目標已經完成。實際上，引導學生進一步探索，把圓的面積推導經驗遷移至圓柱當中，就會有意想不到的收獲。學生通過把圓柱的表面轉化成長方形，實現了立體圖形與平面圖形的“無縫對接”，還進一步強化了空間觀念。

培養學生的空間觀念并非朝夕之功，而需要滴水穿石的韌勁和堅持。在教學中，教師要深入挖掘教材資源，密切聯系現實生活，為學生空間觀念的發展提供大量豐富感性的素材，使學生在動手操作中發展數學思維，在圖形轉化中發展空間觀念，實現“數學思維”與“空間觀念”的“雙豐收”。

（責編 童 夏）