例談勻變速直線運動問題中平均速度公式的運用

浙江 沈 衛

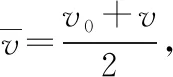
一、勻變速直線運動的實例分析

1.從運動學的基本規律出發解決問題

【例1】如圖1所示，物體靜止在水平地面上，某時刻給它施加一個水平方向的恒力F，使其在水平地面上做勻加速直線運動。可知物體在運動過程中第5個7 s內的位移與第11個3 s內的位移大小之比為

( )

A.2∶1 B.1∶2 C.7∶3 D.3∶7

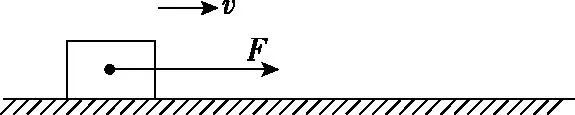
圖1

【分析】物體由靜止開始做勻加速直線運動，v1為第5個7 s初的瞬時速度，也是第4個7 s末的瞬時速度，速度大小滿足v1=a·4t1=28a，因此第5個7 s內的位移x1大小滿足：

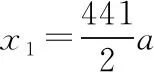
同理，第11個3 s內的位移x2大小滿足：

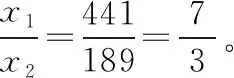
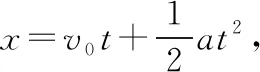
2.由基本規律的遞推關系出發解決問題——運用逐差法計算位移

設第5個7 s內的位移為x5，第1個7 s內的位移為x1，因此有：

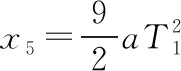
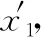
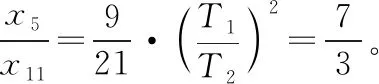
拓展問題已有的解法既是優化答題思路與途徑的重要手段，也是幫助學生拓展知識面、鍛煉思維的重要方式，更是幫助學生在解決問題中樹立信心，形成學習興趣的重要精神來源。同時還能在諸多解法的對比應用中找出最優解法，從而加深對概念的認知、規律的理解、解法的運用。

3.運用平均速度公式得出位移的比值關系

對比上述三種解法，可以看到平均速度公式在解決該問題中的優勢。首先，平均速度公式的運用降低了計算量。平均速度公式依托其物理含義——中間時刻速度，輕易地解決了兩個位移過程的速度關系，避免了平方項的計算；其次，運用平均速度公式確定了上述過程中位移大小之間的關系。任意過程中兩個時間間隔內的位移關系也能夠運用平均速度公式很快地予以確定。因此，教師在運動學模塊的教學中，要重視平均速度公式的相關特點與運用，這將有助于學生對運動學模塊的知識內容與應用產生更為全面的認識。

二、平均速度公式運用的實例分析

1.平均速度公式在復雜的勻變速直線運動問題中的運用

對于常見運動學問題的處理，往往需要在位移x、時間t、初速度v0、末速度v及加速度a這五個物理量已知三個或三個以上才能運用勻變速直線運動的基本規律進行處理，這是學生喜聞樂見的題型。但對于上述條件所給不完全的問題，該如何運用勻變速直線運動規律進行求解呢？

【例2】一個物體做勻加速直線運動，它在第3 s內的位移為5 m，下列說法正確的是

( )

A.物體在第3 s末的速度一定是6 m/s

B.物體的加速度一定是2 m/s2

C.物體在前5 s內的位移一定是25 m

D.物體在第5 s內的位移一定是9 m

【分析】上述條件會使學生產生一個錯覺，前5 s內物體在每1 s的位移滿足1∶3∶5∶7∶9，則第1 s內的位移為1 m，第5 s內的位移為9 m。因此，四個選項都是正確的，答案即為ABCD，顯然，這對于選擇題而言是不符合邏輯的。學生之所以有這樣的錯覺，是把物體運動看成初速度為零的勻加速直線運動，而題干并未說明，即物體運動的初速度可能為零也可能不為零，因此ABD選項錯誤。根據第3 s內位移為5 m可知，第3 s內的平均速度為5 m/s，即第3 s內的中間時刻速度為5 m/s，即前5 s內的中間時刻速度為5 m/s，即前5 s內的平均速度為5 m/s，因此前5 s內的位移一定是25 m，C選項正確。

【例3】做勻減速直線運動的物體4 s停止，若第1 s內的位移為14 m，則最后1 s內的位移是多少？

【分析】運用逆向思維，該問題很明顯滿足位移的比例關系，即第1 s內位移與最后1 s內位移比例關系滿足7∶1，因此最后1 s內位移為2 m。

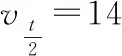
根據逆向思維，最后1 s內的位移為

如果例3中的問題變為物體經3.5 s停止，則在計算最后1 s內發生的位移大小時比例關系就不再不適用了，但平均速度公式仍可以使用。若物體經3.5 s停下，時間Δt=3 s，因此物體的加速度a滿足

顯然平均速度公式在該問題中的運用比位移的比例關系更具普適性，在解決問題中也更能突出問題中運動學的規律與本質。因此在教學活動中，教師適當地向學生傳達平均速度公式的相關巧妙應用，可以幫助學生強化對運動學規律的認識與掌握，增加學生應對難題、解決難題的能力與信心。

2.平均速度公式在處理紙帶數據中的運用

運用打點計時器與紙帶探究勻變速直線運動的規律時，對于紙帶上計數點瞬時速度的計算便是依據勻變速直線運動的平均速度公式。

【例4】某同學用打點計時器研究小車的勻變速直線運動，他將打點計時器接到頻率為50 Hz的交流電源上，實驗時得到一條紙帶如圖2所示。他在紙帶上便于測量的地方選取第一個計數點A，之后每5個點取一個計數點。測量時發現B點已模糊不清，他只測得AC長為14.56 cm，CD長為11.15 cm，DE長為13.73 cm。請問，根據上述數據能否計算出AB的距離。

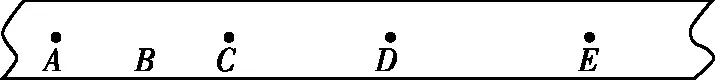
圖2

【分析】雖然B點模糊不清，但是根據已有的數據分析運用逐差法可以得到紙帶的加速度為

同理可知

xBC-xAB=aT2，其中T為相鄰計數點間的時間間隔，T=0.1 s，因此xBC-xAB=0.0258 m=2.58 cm ①

同時AB的距離與BC的距離之和滿足

xAB+xBC=14.56 cm ②

聯立①②兩式即可得到AB與BC的距離分別為

xAB=5.99 cm，xBC=8.57 cm

除了利用逐差法可以確定AB間的距離之外，還可以利用平均速度公式來進行處理。

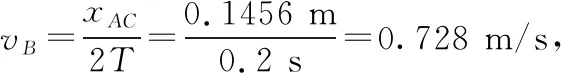
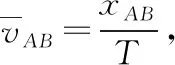
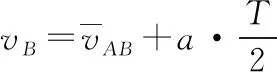
將數據代入表達式③即可求得xAB=5.99 cm

紙帶出現點跡模糊的情況在力學實驗中屬于常見現象，如果運用運動學規律對模糊的點跡進行探討，不僅可以確定模糊的點跡位置，引發學生的興趣與思考，同時還可以深化勻變速直線運動規律在解決實際問題中的運用，加深學生對運動學公式及其變化的認識與理解。

勻變速直線運動規律是構成高中階段物理知識體系的基本框架，是學生學習其他物理模塊知識的必備基礎，同時，平均速度公式也是最重要的知識內容之一。雖然其公式與定理內容并不多，但仔細分析會發現每一個規律與定理都有其獨特的變化與運用。所以即便是簡單的平均速度公式也有在解決具體問題中的多種表現與作用，不可小覷。因此，教師更要注重對基本概念與規律的深挖、深究，促使學生多思考、多探討，從而充分發揮學生的學習能動性，提高學生的學習能力、思維能力與解決實際問題的能力。