四邊形內勃羅卡角的三個公式
2021-04-13 07:22:30山東省濱州市沾化區第一實驗小學256800曹景云山東省濱州學院理學院256600
中學數學研究(江西) 2021年4期
山東省濱州市沾化區第一實驗小學 (256800) 曹景云山東省濱州學院理學院 (256600) 尹 櫪
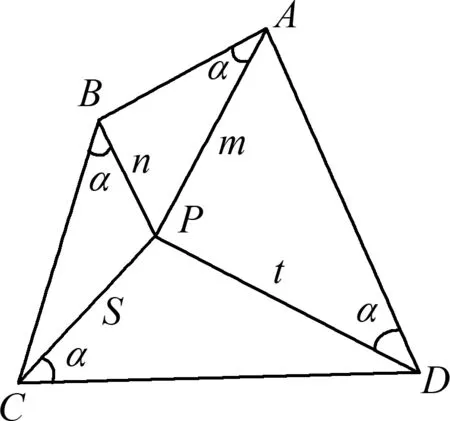
圖1
若在四邊形ABCD內,存在點P使得∠PAB=∠PBC=∠PCD=∠PDA=α,那么點P叫做四邊形的勃羅卡點,而角α稱為四邊形的勃羅卡角.(見圖1)
關于四邊形內勃羅卡點的存在性問題在文[1]中有詳細的討論.本文假設所討論四邊形的勃羅卡點總是存在的.文獻[2]中利用楊學枝的一個性質.給出了凸四邊形內勃羅卡角的一個計算公式,之后文獻[3]中利用正弦與余弦定理給出了四邊形內勃羅卡角的幾個計算公式.本文給出勃羅卡角的三個重要公式,進一步豐富了四邊形內關于勃羅卡角的性質.為了敘述方便,假設四邊形邊AB,BC,CD,DA的長度為a,b,c,d,邊AP,BP,CP,DP的長度分別為m,n,s,t,四邊形ABCD的面積為△.
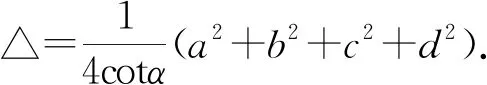
引理2[2]設a,b,c,d為四邊形ABCD的四條邊長,四邊形ABCD的面積為△,則a2+b2+c2+d2≥4△.
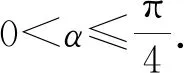
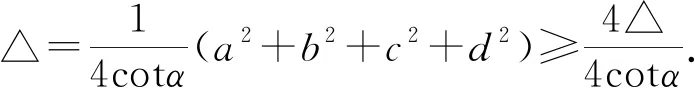
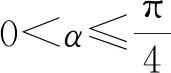
定理2 設角α為四邊形ABCD的勃羅卡角,則sin4α=sin(∠A-α)sin(∠B-α)sin(∠C-α)·sin(∠D-α).
證明:在三角形ABP,BCP,CDP,DAP中利用正弦定理可得
將這八個等式相乘可得
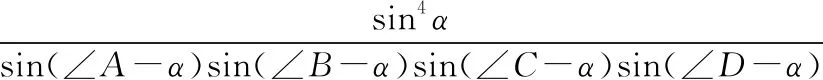
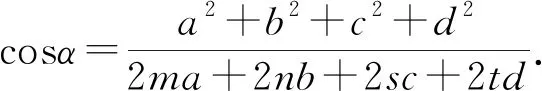
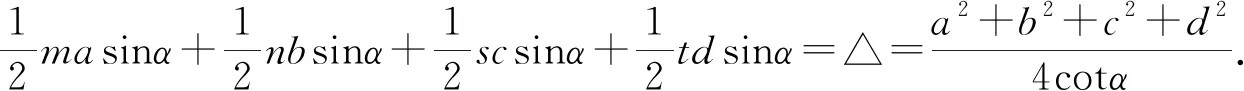
猜你喜歡
山東交通科技(2022年3期)2022-08-05 03:06:24
中等數學(2022年2期)2022-06-05 07:10:50
中國集體經濟(2022年9期)2022-04-12 01:07:35
雜技與魔術(2022年1期)2022-03-16 10:22:48
中學生數理化·七年級數學人教版(2021年11期)2021-12-06 05:38:48
——山東省濟寧市老年大學之歌
老年教育(老年大學)(2021年10期)2021-11-12 09:15:48
小學生學習指導(低年級)(2020年6期)2020-07-25 02:31:36
新生代(2018年23期)2018-11-13 22:41:10
小學生學習指導(低年級)(2018年9期)2018-09-26 05:59:44
瘋狂英語·新讀寫(2018年2期)2018-09-07 09:32:10

