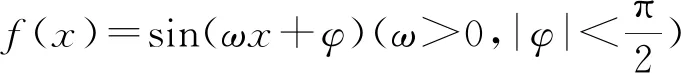抓住三角函數的“五性”速解題

江蘇省金湖中學 (211600) 張太清

在許多與三角函數相關的問題中，如果我們能夠挖掘三角函數中蘊藏的周期性、奇偶性、單調性、對稱性和有界性并有效使用，從而就抓住問題實質、使問題的快速解決，起到事半功倍的作用.下面通過幾個典型題例，展示這些性質的精妙運用給解題帶來的效果，供讀者朋友參考.

一、周期性

若對函數y=f(x)，存在實數T≠0，使等式f(x)=f(x+T)對任意x都成立，則稱此函數為周期函數，T為一個周期.

例1 已知函數f(x)=Asin(ωx+φ)(A>0,ω>0,0≤φ≤π)一個周期內圖像的最高點是(2,2)，與它相鄰的最低點的橫坐標是6，則f(1)+f(2)+f(3)+…+f(2020)=.

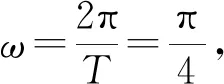
評注：求一些函數式若干項的和的問題，找出其式子規律性(如周期性)是非常重要的思維趨向.

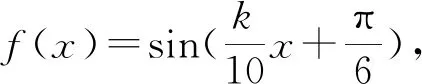
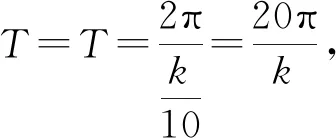
評注：抓住所給周期的范圍就是抓住了問題的關鍵點，為后面快速解題鋪平了道路.

二、奇偶性

若函數y=f(x)，若對定義域內的任意x都有f(-x)=f(x)，則稱函數f(x)為偶函數；若對定義域內的任意x都有f(-x)=-f(x)，則稱函數f(x)為奇函數.

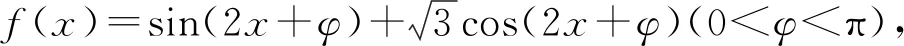
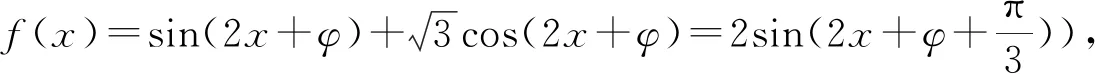
評注：對于一般的三角函數式，若需判斷函數的奇偶性、單調性或求函數的最大值和最小值等問題時，首要任務是將其轉化為f(x)=Asin(ωx+φ)的形式，然后再根據條件求解.

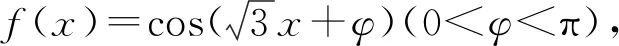
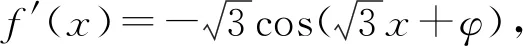
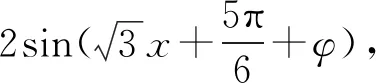
評注：此題是三角函數與導數的綜合題，體現了高考題的考查目標與方向，抓住三角函數為奇函數的特點解決參數求值問題是破題的關鍵.

三、對稱性

對于函數y=f(x)，若在定義域內任意x，都有f(a-x)=f(a+x)成立，則稱此函數關于直線x=a對稱；若都有f(a-x)=-f(a+x)成立，則稱此函數關于點(a,0)對稱，其中偶函數與奇函數是這兩種情況下在a=0時的特例.

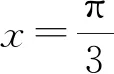
評注：由于三角函數y=sinx的對稱軸是比較熟悉的，所以這里判斷出所給函數是軸對稱問題就是解題的重要環節.

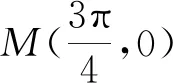
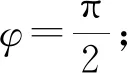
評注：將中心對稱的條件轉化為一個等式，再分析化簡這個等式，求出待求參數的值是解決此類題最基本的思路.

四、單調性

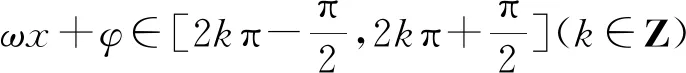
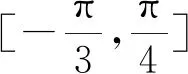
評注：已知函數的單調區間求其它問題，就是將已給的區間看成是整個函數區間的子集，然后建立等式或不等式解決問題.

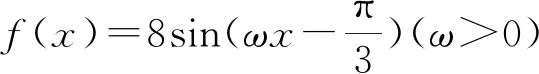
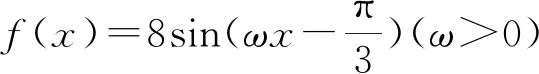
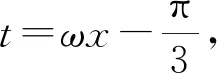
五、有界性

如果函數y=f(x)對給出的區間上任意x都滿足f(x)≤M，則稱M是此函數的上確界，滿足f(x)≥N，則稱N是此函數的下確界.