中點在解析幾何問題中的三種用法
甘肅省天水市第八中學 (740120) 王存斗
中點問題是解析幾何中最常見的題型之一,而如何用中點?如何求中點?學生可能沒有成熟的經驗和具體的措施,為此,本文從優化解題的角度來探討中點在解析幾何中的三種用法,供讀者參考.
一、抓住中點的幾何特征
中點的幾何性質非常明顯,也常隱藏在圓心、對稱、平行四邊形等條件中,如果能在解題中充分發揮它的幾何作用,可使解題過程進一步優化.
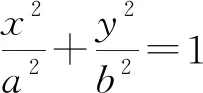
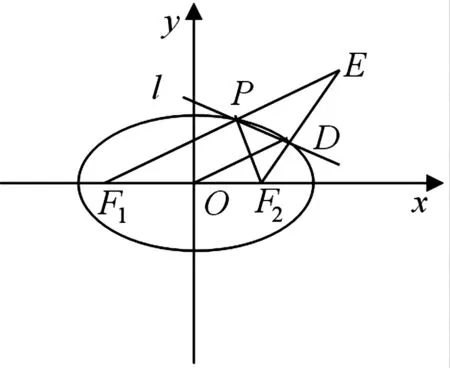
圖1

評注:由于D點是兩直線的交點,很多同學都會想到“交軌法”求其軌跡方程,但本題若用此法,運算就會過于繁雜.而本解法是在理解題目內涵的基礎上,巧用F1F2的中點是O的幾何性質,就使整個解題變得輕松流暢.

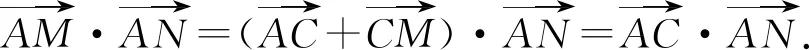
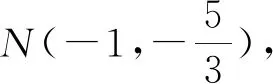
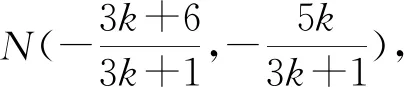

二、用中點巧求斜率
在許多問題中需要表示出直線方程,先找到斜率是非常重要的,如果所在的直線上含有已知的中點,那么就可以通過分別設點代入曲線方程,再二式相減就能夠得到此直線的斜率了.
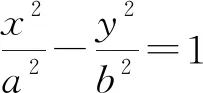
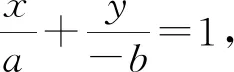
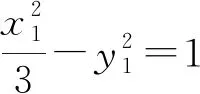
評注:求直線的斜率的方法有很多,但若方法的選擇不當將會導致繁瑣的運算,令人望而卻步.此解法通過巧妙設出中點坐標,利用圓及等腰三角形的性質,使問題獲得簡解.
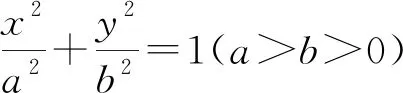
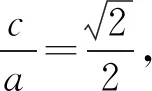
評注:此解法通過挖掘得到圓心就是線段AB的中點并加以充分運用,直線AB的方程就求出來了,這就是“點差法”的典型用法.
三、用參數表示中點
通過將直線方程與曲線方程聯立,消去一個未知數,使之轉化為一個一元二次方程,再由根與系數的關系得到中點坐標,這是中點最常用的方法.
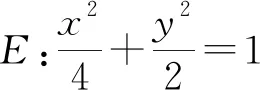
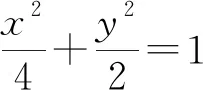
評注:表示中點坐標是問題解決的關鍵.聯立方程,再由根與系數的關系求出中點是圓錐曲線問題中的常見解題步驟.
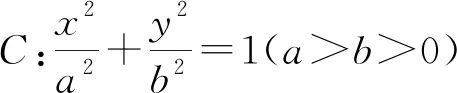
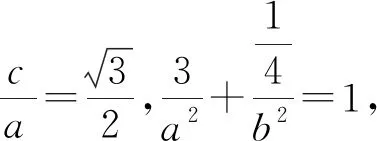
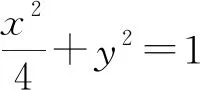
評注:此解題過程中用到了解析幾何中許多解題技巧,如怎么表示中點、如何解決面積的表達式、如何求最值等,我們只有通過不同題型的長期訓練,才能有效的掌握這些.
上面是對解決解析幾何問題中如何使用中點的一個歸納,以例說事,經典實用.我們在平時的教與學中,要引導學生不斷總結歸納,注意有條理的擴大知識儲備,這樣才能提升教學效果,使學生獲得更多的收獲.

