處理三角函數中參數ω范圍問題的基本意識*

華南師范大學附屬中學汕尾學校 (516600) 劉光明

近年高考題中常出現根據三角函數圖象判斷周期范圍或通過周期確定參數ω的范圍及巧用零點確定ω的取值等問題.本文基于參數ω的取值范圍試題，從三角函數的單調性、對稱性、最值、零點、不等式等知識融合角度剖析解決參數ω取值范圍問題的基本解答思路.通過例題的闡述，反思和提煉出子集意識、數形結合意識和整體意識等三種處理此類問題的基本意識.

1 子集意識

三角函數單調性與參數ω的取值范圍相結合是一種比較常見的命題方式，在2012年、2016年、2018年和2019年全國卷中都出現過.處理此類問題的一般想法是先根據題意所已知的函數f(x)單調區間A，求出原函數相應的單調區間D，根據A?D得到一個不等式組，通過解不等式組自然得到相應的取值范圍，如此處理問題的思維就是子集意識.

例1 (2018年全國卷Ⅱ文10)若f(x)=cosx-sinx在[-a,a]是減函數，則a的最大值是( ).

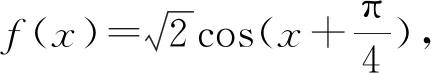
評注：例1也可以充分借用選項中的一些特殊數值進行試探，代值檢驗，僅僅限于選擇題，不是一般做法.根據所已知的函數f(x)單調減區間[-a,a]求出原函數相應的單調減區間D，根據[-a,a]?D這個子集關系得到不等式組，通過解不等式組自然得到相應的取值范圍，此法才是處理三角函數單調區間問題與參數范圍的一般方法.

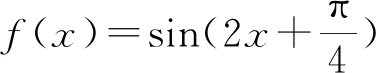
例2 (2015年天津文14)已知函數f(x)=sinωx+cosωx(ω>0)，若函數f(x)在區間(-ω,ω)內單調遞增，且函數f(x)的圖象關于直線x=ω對稱，則ω的值為.

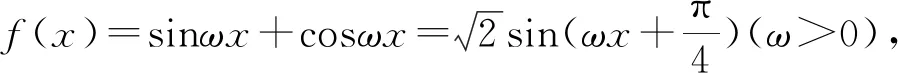
評注：例2依然是區間上的單調性問題求參數ω范圍，故應用子集意識求解.但也可以根據函數f(x)在區間(-ω,ω)內單調遞增，函數f(x)的圖象關于直線x=ω對稱得到函數在x=ω處取得最大值進行解答.

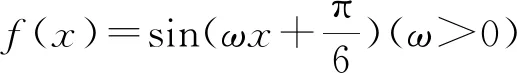
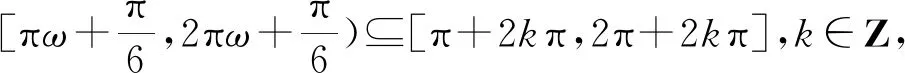
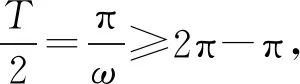
2 數形結合意識

所謂數形結合意識，就是根據所已知的函數性質，大致描繪出函數圖象，然后從圖象中分析出相關函數性質，從而得到參數ω的不等關系.三角函數具有無數條對稱軸和無數個對稱中心，是一個特殊的周期函數，因此三角函數性質之間具有一種深藏不露的奇妙關系，值得挖掘和應用.

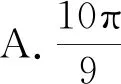
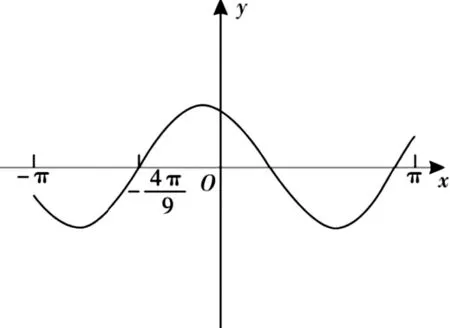
圖1

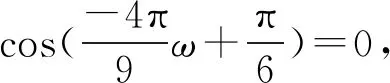
評注：此題不避諱常考知識點，稍有創新，巧用圖象呈現出函數的性質，考查讀圖能力，充分體現數形結合思想.

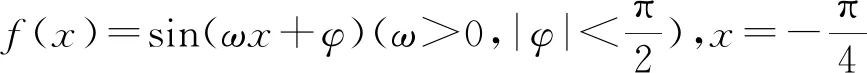
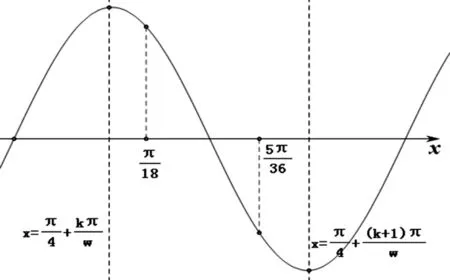
圖2

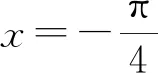
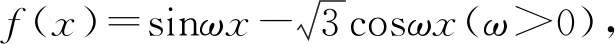
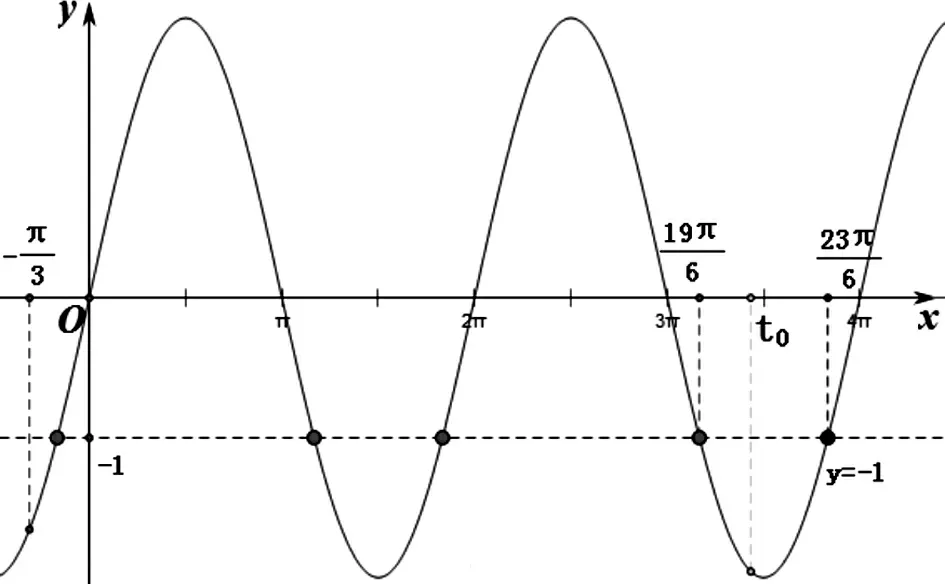
圖3

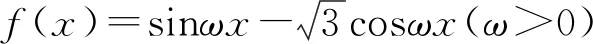
3 整體意識

整體意識就是將函數f(x)=Asin(ωx+φ)中的“ωx+φ”看作一個整體，從而將f(x)轉化為熟悉的函數y=Asint，根據y=Asint的圖象和已知的函數性質進行分析，遵循先定后動原則，借助數形結合意識進行求解.

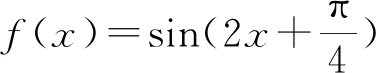
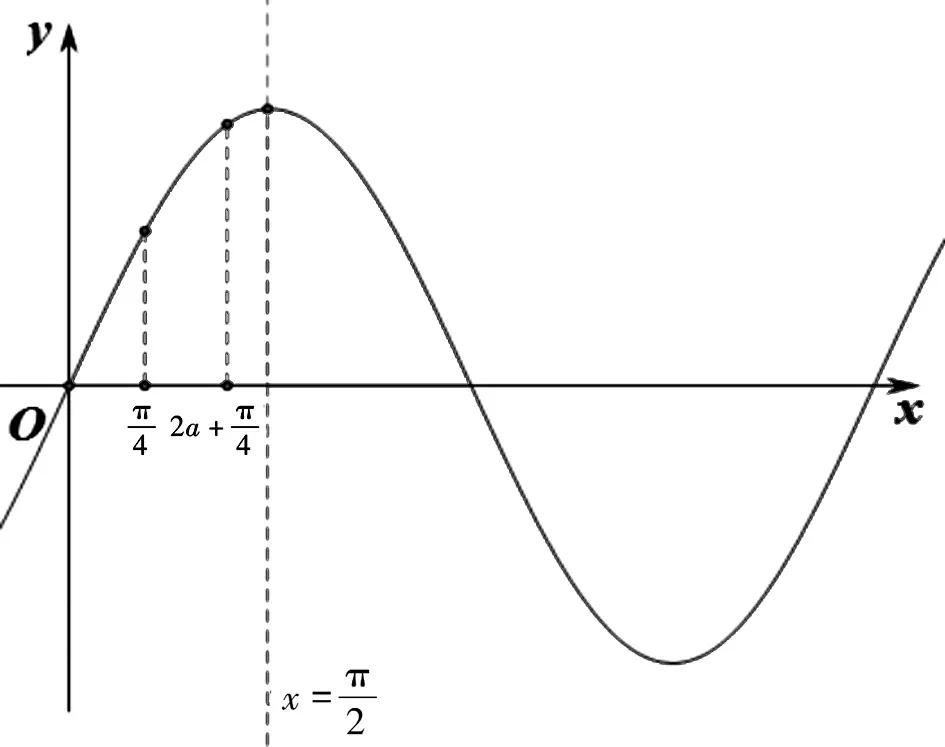
圖4

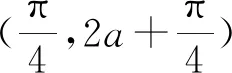
變式1 已知函數f(x)=2sinωx(cosωx+sinωx)(ω>0)的圖象在區間[0,1]上恰好有一條對稱軸和一個對稱中心，則參數ω的取值范圍是.

圖5

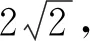
A.4 B.5 C.6 D.7

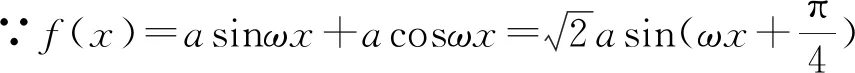
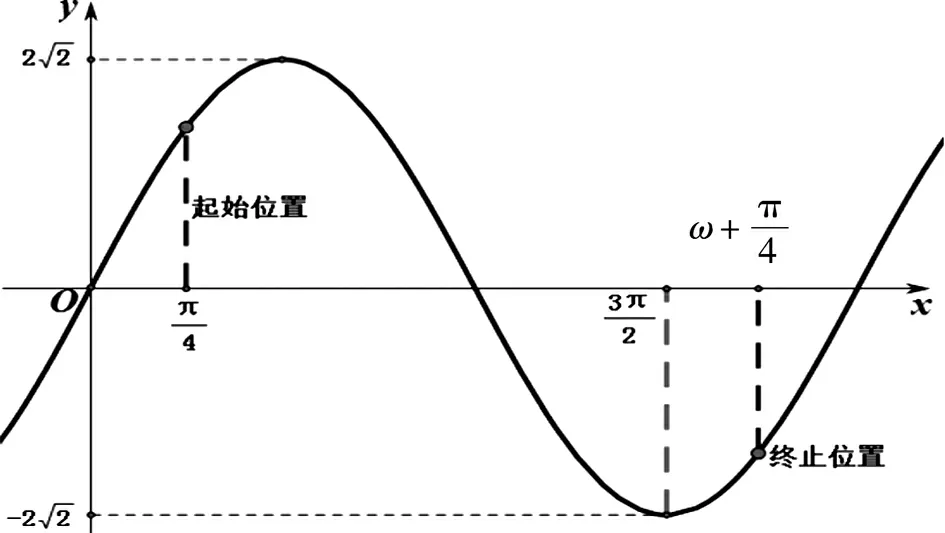
圖6

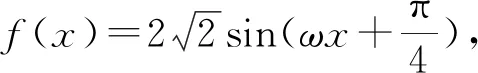
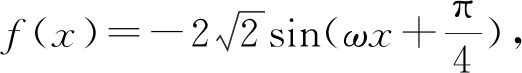
綜上所述，正整數ω的最小值為4.

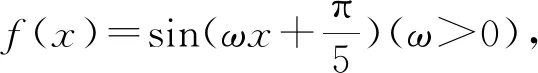
圖7