形助探究思路 數精嚴謹推理*

安徽省宿州市碭山中學 (235300) 高 凱

數形結合思想是數學的重要思想之一，它是發現問題和提出問題，分析問題和解決問題的重要手段，是探索和形成論證思路，進行數學推理，構建抽象結構的思維基礎.

一、試題再現

題目(2020年“皖北協作區”第22屆高三聯考理科第21題)已知函數f(x)=ax2-2lnx(a∈R).(1)當a=1，證明f(x)≥x-lnx;(2)是否存在不等的正實數m,n滿足m=n2且f(m)=f(n)，若存在，求a的取值范圍；若不存在，說明理由.

二、解法探究

分析：(1)略；(2)由題m=n2及f(n)=f(m)得am2-2lnm=am-lnm，即am2-am-lnm=0,由于m,n為不等的正實數，問題轉化為關于x的方程ax2-ax-lnx=0有不等于1的實根.

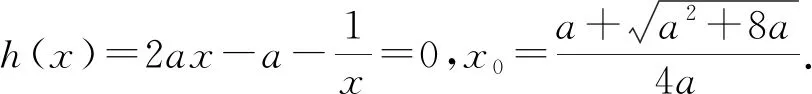
綜上所述，a的取值范圍是{a|a>0且a≠1}.

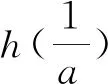
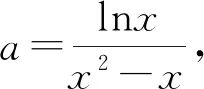
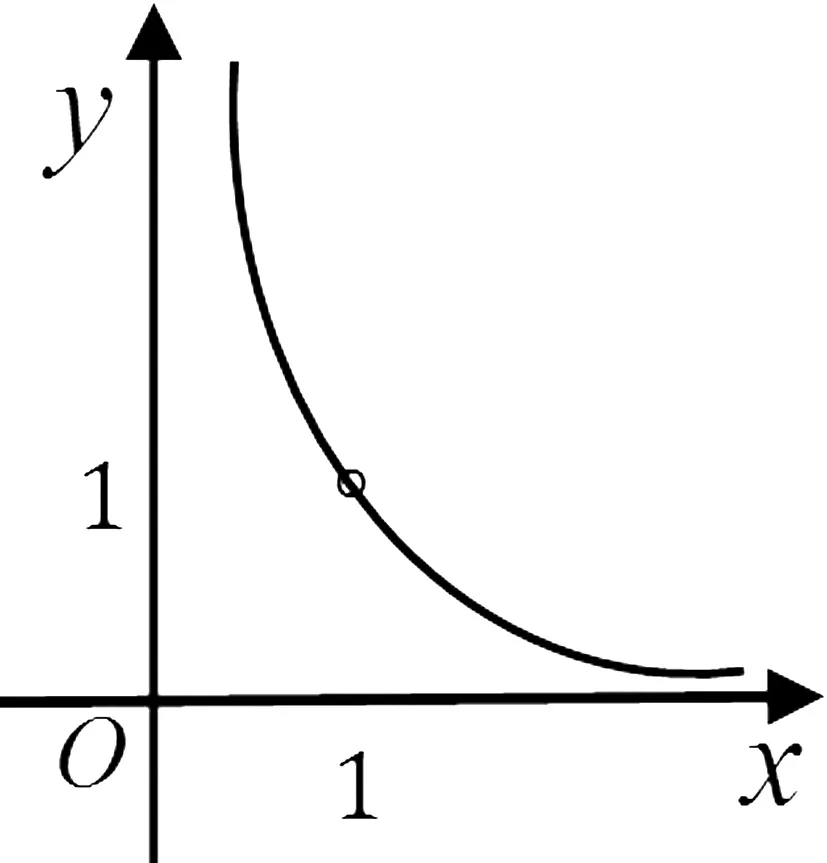
圖1

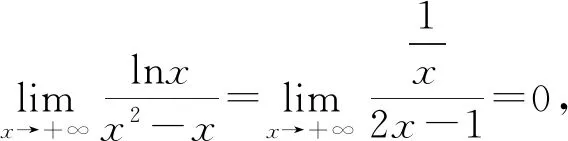
{a|a>0且a≠1}.

評析：分離參數a后，避免了參數討論，學生更容易接受和理解，但是美中不足的是高中階段不要求掌握洛必達法則.

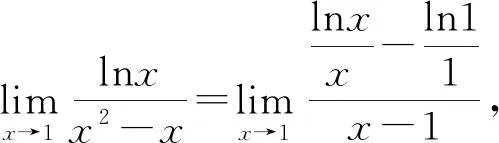
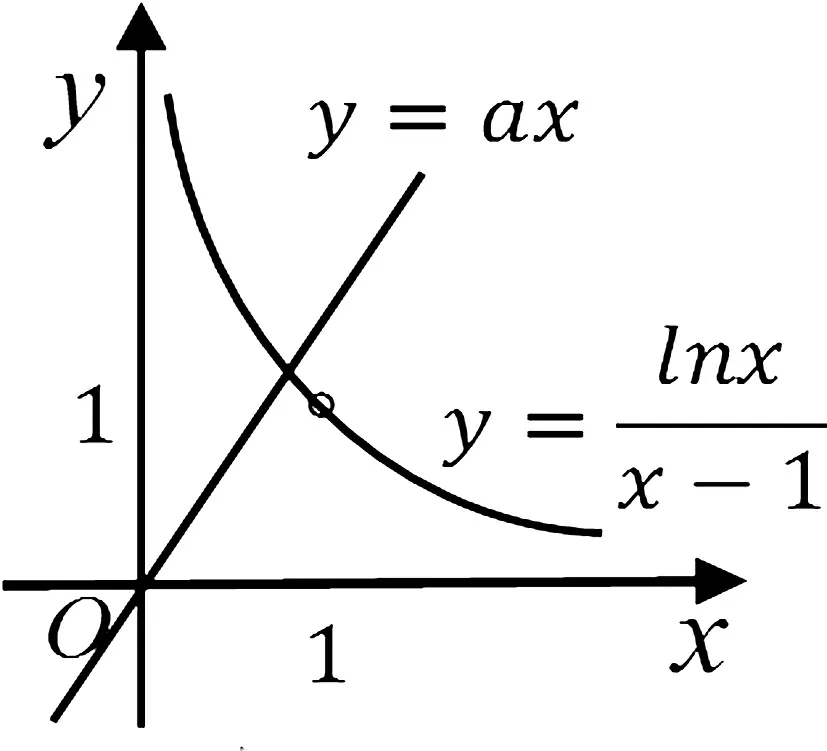
圖2

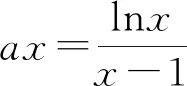
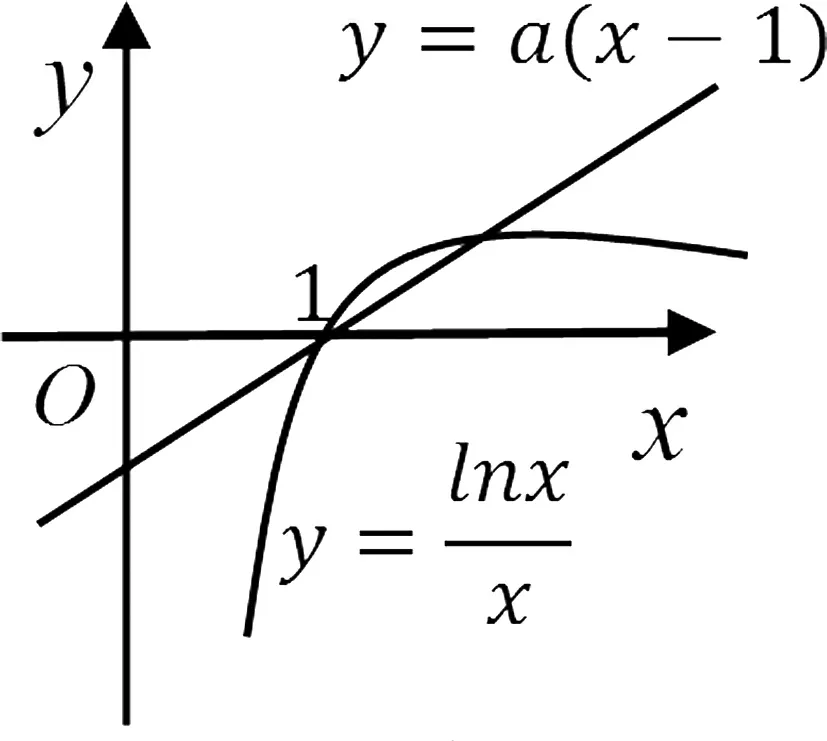
圖3

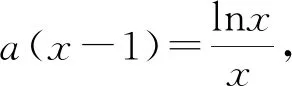
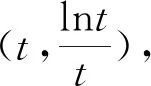
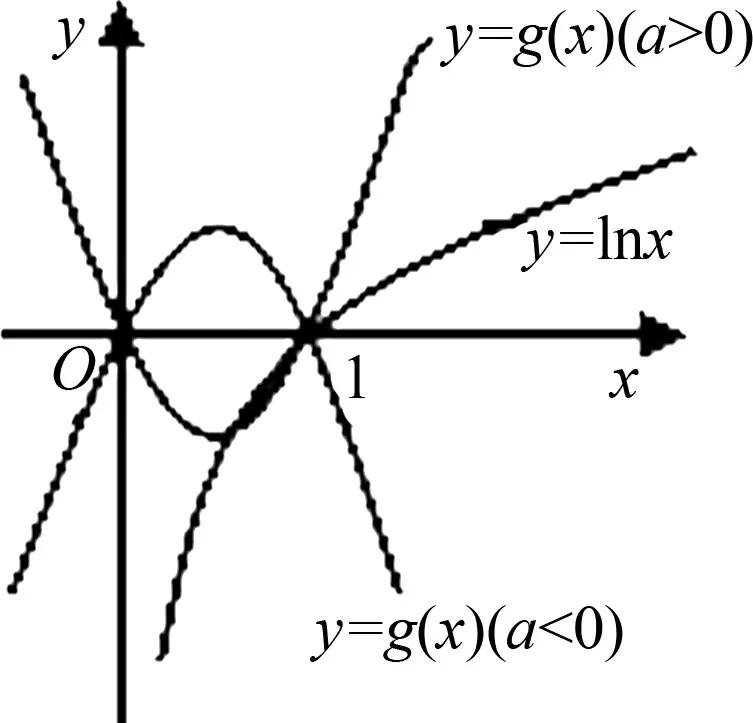
圖4

方法5:由題得a(x2-x)=lnx.令g(x)=a(x2-x);h(x)=lnx,兩函數的圖象如圖4所示.當a≤0時，兩函數的圖象只有一個交點(1,0)，不符合題意.

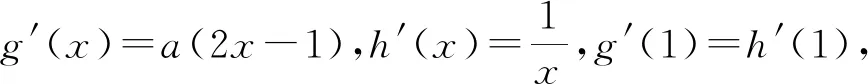
評析：把抽象問題和直觀的圖象結合起來，通過圖象化抽象為直觀，易于發現解決問題的思路；然后結合圖象進行推理論證，從而達到精確化，理性化的理解.

三、心得體會

華羅庚曾說：“數缺形時少直觀，形少數時難入微，數形結合百般好，隔裂分家萬事休.”

數形結合的思想正是把“最活躍的形象思維”與“最嚴密的邏輯思維、代數推導”結合起來理解問題、解決問題的一種思想方法.教學時我先用幾何畫板作出不同解法構造出的函數圖象，先讓學生直觀感受圖形的變化與運動的規律，然后進行數學推理.方法1推理嚴謹，但過于抽象，對學生能力要求較高，得分率低；方法2，方法3轉化為圖象解題，形象直觀，容易發現思路，但需準確畫出圖象.方法4，方法5從圖象的位置關系入手，利用切線研究問題，需從圖象變化中尋找分類討論的切入點.

通過學習，提升學生利用圖象分析問題，建立形與數的聯系，探索解決問題的能力，增強他們運用幾何直觀和空間想象思考問題的意識，進而感悟數學的本質.