最大公因數與最小公倍數方法探討

【摘要】在求兩個數的最大公因數時，新課標明確指出不再由公因數或最大公因數，引進互質數的概念，是精簡數論初步知識的一個具體體現。而《標準》中有關求最大公因數的要求是：“能找出兩個自然數的公因數和最大公因數”。建議學生采用“找”的方法，不再需要分解質因數與短除法。事實上，即便在過去學了分解質因數和短除法之后，也極少有學生在約分時用到。這一改進，雖說大大降低了學生學習的難度，但在教學中，筆者在課堂上和學生把其中的各種規律性知識與解決方法歸攏后，很多學生對本部分的知識能夠做到進一步系統化，解決方法多樣化[1]。

【關鍵詞】質數? 合數? 互質? 質因數

【中圖分類號】623.5? ? ? ? ? 【文獻標識碼】A 【文章編號】2095-3089（2021）41-0104-02

筆者在教學過程中發現學生在尋找兩個數最大公因數時，方法過于單調，幾乎是機械化去找、去操作。而且在碰見一些稍復雜的因數時，往往存在丟失現象，最后導致錯誤連連。針對最大公因數的求法問題，筆者認為完全可以發動學生多渠道去求，不必拘泥于一標，畢竟本節內容和后面的約分、最小公倍數、通分有太多聯系。聯系日常教學實際，結合一些習題和資料，筆者針對本部分進行了簡要梳理，期望對學有余力的孩子有所幫助，也望同行指正交流。

一、最大公因數的幾條探索性規律及解決方法

1.互質的兩個數最大公因數是（以下情況均是互質的情況）

（1）1與其他任意自然數互質。

（2）2和任何奇數都互質。

（3）連續的兩個自然數互質。.

如：8和9;14和15;111和112……

（4）相鄰的兩個奇數互質。

（5）不同的兩個質數互質。

如：5和7;7和19;31和89……

（6）當一個是合數，一個為質數時（合數不是質數的倍數），這兩個數互質。

2.當兩個數成倍數關系時，小的那個數就是這兩個數的最大公因數[2]。

如：4和8;16和32……。

3.兩個數的所有公因數都是最大公因數的因數（最大公因數是所有公因數的倍數）。如18與27的公因數有1、3、9。其中他們的最大公因數9也是其他公因數1、3、9的倍數。本條結論筆者認為，可以讓學生以此來判斷自己所找的最大公因數是否合適。

二、其實除了以上幾種方法外，在尋找兩數最大公因數時還可以采用以下幾種方法[3]

1.列舉法求18與27的最大公因數：

先分別找出18和27的因數，然后看18和27的因數中公有的部分，再從中找出最大的一個。

例如：求18與27的最大公因數。

18的因數有：1、2、3、6、9、18。

27的因數有：1、3、9、27。

18與27的公因數有：1、3、9。

18與27的最大公因數是9。

2.篩選法求18與27的最大公因數。

可以先找出18的因數，再在這些因數中圈出27的因數，進而找出兩者最大的那個因數。

18的因數：①，2，③，6，⑨，18。

在18的因數中，1，3，9是27的因數，自然9是18和27的最大公因數。

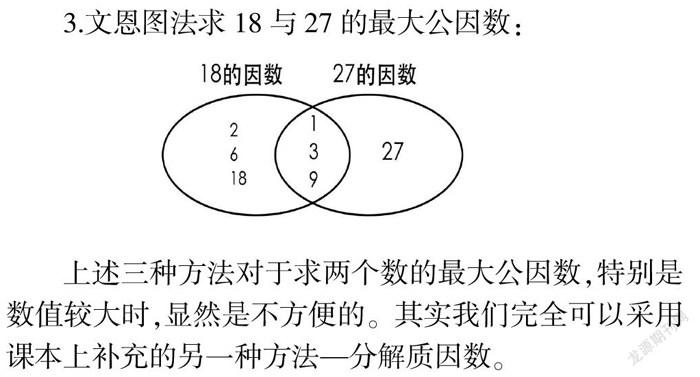
3.文恩圖法求18與27的最大公因數：

上述三種方法對于求兩個數的最大公因數，特別是數值較大時，顯然是不方便的。其實我們完全可以采用課本上補充的另一種方法—分解質因數。

4.分解質因數法求18與27的最大公因數。

首先我們把18和27分別分解成幾個質數相乘的形式，18=2×3×3，27=3×3×3。因為18和27的公因數必定包含18和27公有的質因數，而最大公因數是其中最大的一個。自然它必須包含18和27共有的質因數3與3，這樣3乘3就是18和27的最大公因數。

18=2×3×3

27=3×3×3

鑒于上面的方法，我們還可以用經典的做法——短除的形式找到公因數和最大公因數。

5.短除法求18與27的最大公因數。

首先用3（18和27的最小質因數）去除這兩個數，看除完的商是否互質，如果不互質，接著繼續用他們的公因數（質數）往下除，一直除到商互質為止，然后把所有除數相乘，得到的積就是18和27的最大公因數。

與前邊的分解質因數法相比較，我們不難發現：他們結果相同，而短除法所用到的兩次除數正是這兩數的公有質因數。而這兩個數的最大公因數，則是這兩個數的公有質因數的連乘積。無疑給學生的學習帶來了一絲新意。

在通過短除法求出最大公因數9后，我們結合第三條規律——最大公因數是所有公因數的倍數（所有的公因數都是最大公因數的約數），依次求出他們的其他公因數——1，3，當然我們也可以借助短除法解決三個數或者更多數的最大公因數問題。

6.縮小倍數法求18與27的最大公因數。

當把18縮小到原來的1/2時，發現9恰好也是27的因數，通過進一步驗證會發現9是18與27的最大公因數，同樣的研究策略，我們可以按照相同的方法求得兩個數或者三個數的最小公倍數。

雖說在教學過程中，我們不要求學生對知識過于求全求深，但作為從教者來說，讓我們把知識內涵研細，研透。夯實了個人素養才會讓孩子們“人人都能在數學上獲得發展，不同的學生獲得不同發展”。

三、結語

準確快速地求出兩個數的最大公因數與最小公倍數的學習是學生很難掌握的內容，又是至關重要的。通過研究不難發現：當兩數成倍數關系或互質關系時可直接寫出它們的最大公因數或最小公倍數，當既要求最大公因數又要求最小公倍數時，用短除法或分解質因數法比較簡便;當只求最大公因數時，用短除法或縮小倍數法比較簡便;當只求最小公倍數時用大數翻倍法比較簡便，當兩個數比較大，比較復雜時，用短除法比較簡便。

總之在探求最大公因數與最小公倍數時，需要學生看清數字之間關系，看清數據特征，看清條件與要求，用好最佳方法，認真細心計算，才能減少后期的計算迷茫。

參考文獻：

[1]中華人民共和國教育部.義務教育數學課程標準[S];北京師范大學出版社，2012-1

[2]劉來剛.名師解教材 五年級數學下 人教課標改進版[M].吉林大學出版社，2011.04

[3]吳國和.求最大公因數和最小公倍數的幾種方法[J].數學大世界（小學五六年級適用），2011-Z2（24）

作者簡介：

胡順治（1980年8月26日-），男，漢族，江蘇省連云港市人，大學學歷，一級教師（中一），研究方向：數學教育教學與班級管理。