基于對偶四元數的捷聯慣導算法在發射點慣性系下的應用研究
杜 鵬,楊 靜,邱紅專,熊 凱
(1.北京航空航天大學自動化科學與電氣工程學院,北京 100083;2. 北京控制工程研究所,北京 100081)
0 引言
對于運行在高動態環境下的載體而言,捷聯慣性導航系統的性能容易受惡劣環境的影響,在姿態解算的過程中,由于有限轉動的不可交換性,不可避免地存在著由圓錐運動引起的圓錐誤差;在速度解算的過程中,由于運載體同時存在線運動和角運動,當采用速度增量進行解算時,也必須考慮到系統的劃船誤差的影響。傳統的捷聯慣導算法通過對圓錐誤差和劃船誤差分別設計相應的算法進行補償來提高算法的精度[1]。文獻[2-3]針對速度解算中產生的劃船誤差,在東北天導航坐標系下設計了不同的算法進行補償。而針對姿態解算中產生的圓錐誤差,文獻[4-6]針對不同的陀螺設計了基于角增量和角速度的圓錐效應補償算法。
在傳統的導航算法中,對劃船誤差和圓錐誤差分別設計算法進行補償,采用了傳統的運動學觀點,將剛體的旋轉與平移分開進行考慮。而對于剛體來說,旋轉與平移實際上是同時進行的,有學者提出了可以利用相關公式將圓錐補償算法轉換為劃船誤差補償算法[7-9],但這并不容易在實際的導航算法中實現,而研究發現劃船誤差補償算法與圓錐誤差補償算法存在一定的等價性,其補償原理和過程大致相同。而由Clifford在對偶數基礎上提出的對偶四元數,提供了一種可以同時描述旋轉和平移的工具。文獻[10]將對偶四元數應用于慣性導航解算,推導了更為簡單直觀的基于對偶四元數的慣導微分方程。
對偶四元數導航算法能同時對劃船誤差與圓錐誤差進行補償,可以在一定程度上提升導航算法的性能。目前已公開發表的文獻大多是以飛機等載體為對象,在東北天導航坐標系下對對偶四元數導航算法展開研究的[11];而運行在高動態環境下的彈道導彈等載體,通常采用發射點慣性坐標系作為導航坐標系,相關研究并不多見。本文將在發射點慣性系下,對基于對偶四元數的捷聯慣導算法展開研究。
論文的結構安排如下,首先介紹了發射點慣性系下的捷聯慣導解算模型,在此基礎上推導了發射點慣性坐標系下對偶四元數算法的解算公式,比較了速度更新過程中對偶四元數算法與傳統算法的精度差異。并設計了多條機動飛行軌跡,以三子樣算法為例,對對偶四元數算法和傳統算法的性能進行了仿真對比分析。
1 發射點慣性系下捷聯慣導解算
1.1 坐標系說明
將文中用到的主要坐標系定義如下:
1)發射點慣性坐標系oxliylizli:坐標原點位于初始時刻的發射點;oxli軸是發射垂直面與發射點當地水平面的交線;oyli軸垂直于oxli軸,指向天;ozli軸與oxli軸、oyli軸垂直;且oxliylizli構成右手定則,在慣性空間保持不變,以下簡稱發射點慣性系。
2)載體坐標系oxbybzb:坐標原點位于載體質心;oxb軸與載體縱軸一致,指向機頭方向;oyb軸垂直于oxb軸,位于載體縱對稱面內,指向上方;ozb軸與oxb軸、oyb軸構成右手定則。
3)地心慣性坐標系oxcyczc:地球坐標系oxeyeze在發射瞬時所固定的坐標系。
1.2 解算方法
在發射點慣性系下,建立捷聯慣導的微分方程如下
(1)
(2)
(3)
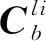
根據上述發射點慣性下的捷聯慣導微分方程,利用加速度計測量的比力和陀螺測量的角速度,分別通過速度更新和位置更新、姿態更新兩個主要環節可以實現對導航參數的遞推解算。
1)速度和位置更新
通過求解式(1)和式(2)實現速度和位置的更新。為此,需要將載體坐標系下的比力轉換到發射點慣性系下
(4)
求解重力加速度在地心慣性系下的分量
(5)
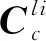
(6)
(7)
由式(4)和式(5)可以計算得到發射點慣性系下的加速度
(8)
對式(8)積分就可以解算出速度和位置
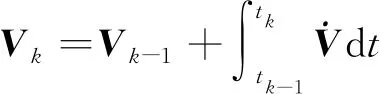
(9)
2)姿態更新
根據描述姿態方式的不同,姿態更新算法有歐拉角法、方向余弦法和四元數法。由于四元數法算法簡單、計算量小、無奇點,因此,在姿態更新中得到了廣泛應用。對式(3)求解就可以對四元數進行更新。
在開始進行姿態更新時,需要對四元數進行初始化,這里可以利用載體在初始狀態下的歐拉角初值來解算四元數初值。
若載體三次轉動對應的歐拉角順序是俯仰角φ0、航向角ψ0和滾轉角γ0,即載體從發射點慣性系到載體坐標系的轉動過程如下
由此可以得到由歐拉角表示的發射點慣性系到載體系的姿態轉換矩陣為
(10)
對應的四元數的初值為
q1=cos(γ0/2)cos(ψ0/2)cos(φ0/2)+
sin(γ0/2)sin(ψ0/2)sin(φ0/2)
q2=sin(γ0/2)cos(ψ0/2)cos(φ0/2)-
cos(γ0/2)sin(ψ0/2)sin(φ0/2)
q3=cos(γ0/2)sin(ψ0/2)cos(φ0/2)+
sin(γ0/2)cos(ψ0/2)sin(φ0/2)
q4=cos(γ0/2)cos(ψ0/2)sin(φ0/2)-
sin(γ0/2)sin(ψ0/2)cos(φ0/2)
(11)
對微分方程進行求解就可以對四元數進行更新。
2 基于對偶四元數的捷聯慣導算法
當載體處在高動態的環境中時,由于有限轉動的不可交換性,在姿態解算中不可避免地存在著由圓錐運動引起的圓錐誤差;在速度解算的過程中,也必須考慮到系統的劃船誤差的影響。傳統的運動學觀點是將兩者分開進行考慮,而對偶四元數可以統一考慮圓錐誤差與劃船誤差進行補償。
2.1 對偶四元數
對偶數是由W.Clifford在1873年提出的,因其形式類似于復數,可以看作是復數域的擴充。其形式如下[12-14]

(12)
其中,α為對偶數的實數部分;α′為對偶數的對偶部分;ε為對偶數單位,且必須有:ε2=ε3=,…,0。
剛體在空間中的旋轉和平移可以用圖 1表示,剛體繞過點c的單位向量l旋轉θ角后,沿l的方向平移距離d(或者先沿l的方向平移距離d后,再旋轉θ角)。
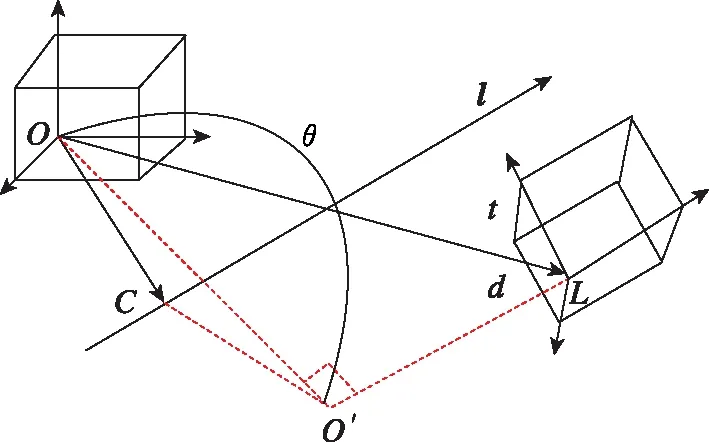
圖1 剛體在空間的旋轉與平移Fig.1 Rotation and translation of rigid bodies in space
剛體的這種運動類似于螺釘和螺母的運動,因此又被稱為螺旋運動,可以用螺旋矢量統一表述,螺旋矢量定義為
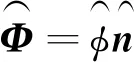
(13)
其中,單位螺旋軸為
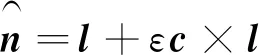
(14)
對偶角為
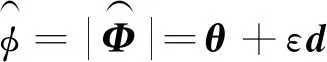
(15)
對偶四元數是以對偶數和四元數為基礎的。其定義如下
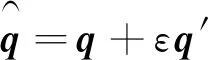
(16)
其中,ε為對偶數單位,q和q′都是普通的四元數
q=q0+q1i+q2j+q3k
(17)
q′=q4+q5i+q6j+q7k
(18)
在圖 1中,平移和轉動分別對應以下關系
tL=q*°to°q
(19)
to=q°tL°q*
(20)
其中:to=[0,to]為零標量的四元數。
根據以上關系,對偶四元數可以表示為如下形式
(21)
其中,實部q是描述轉動的規范四元數;對偶部q′是轉動四元數和平移向量的函數。
對偶四元數可以由螺旋運動的參數表示為
(22)
由式(19)和式(20)可得
to=2q′°q*tL=2q*°q′
(23)
對偶四元數微分方程為
(24)
式中,對偶向量為
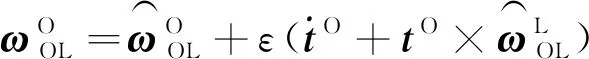
(25)
與傳統四元數更新算法類似,運用螺旋矢量來更新四元數。螺旋矢量的微分方程如下

(26)
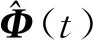
(27)
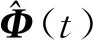
(28)
因此,式(27)可表示為
(29)
對式(29)在時間間隔[tk,tk+1]內積分得到
(30)
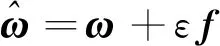
εf(τ)]dτ]×[ω(t)+εf(t)]}dt
[ω(t)+εf(t)]}dt
=Δθm+εΔVm+Φcon+εΔVsculm
(31)
式中
(32)
其中,Φcon和ΔVsculm分別代表圓錐誤差和劃船誤差。從式(32)可以看出,對偶四元數算法將旋轉和平移統一起來,能夠同時補償圓錐誤差和劃船誤差。
與旋轉矢量法類似,螺旋矢量的計算也由單子樣、雙子樣和三子樣等相應的優化算法來完成,其優化系數與等效旋轉矢量法的優化系數完全相同,在得到螺旋矢量后就可以用其來更新對偶四元數。下面以三子樣算法為例,給出對偶四元數的更新步驟為:
螺旋矢量三子樣優化算法
(33)
步驟二:由式(22)可得
(34)
將對偶四元數實數部分和對偶部分拆開得
(35)
將得到的螺旋矢量代入式(35),計算q(ΔT)和q′(ΔT)。
步驟三:設tk+1時刻的對偶四元數可表示為
(36)
將式(36)按照定義拆分成標量部分和對偶部分得到
(37)
將得到的q(ΔT)和q′(ΔT)代入式(37),計算tk+1時刻的對偶四元數。
與東北天坐標系下對偶四元數的更新不同,在發射點慣性系下,不用再考慮地球自轉的影響,也不用再利用分離坐標系的思想,所有的更新均在發射點慣性系下進行。
2.2 對偶四元數初始化
任意一種捷聯慣性導航算法都要有一個迭代遞推的過程,由前一時刻的導航信息推算得到當前時刻的導航信息。在傳統的導航算法中,進行解算時需要知道初始時刻的三軸速度、位置及姿態角(俯仰、偏航、滾轉角)。而利用對偶四元數進行解算時,需要的初始信息為同時包含平動和轉動信息的初始對偶四元數。
對偶四元數實部的初始化與1.1節中姿態更新一樣。
對偶四元數對偶部的初始化如下
(38)
其中,Vli(0)為初始時刻載體在發射點慣性系下的速度。
2.3 速度更新算法比較
在傳統的速度更新算法中,兩個時刻之間的速度增量為
(39)
對于對偶四元數來說,由式(23)可得對偶四元數更新算法的速度增量為[14]
(40)
將式(40)中的三角函數取四階近似,并忽略高階小量,則在對偶四元數更新算法中速度增量的計算公式如下
(41)
將式(31)代入式(41)可得
[(Δθm+Φcon)×(ΔVm+ΔVsculm)]
(42)
與式(39)相比,對偶四元數速度更新算法中速度增量的計算增加了式(42)右邊的后四項,這四項說明了對偶四元數計算的速度增量更為準確,從而提高了速度更新的精度。
3 仿真驗證
為了驗證對偶四元數導航算法的性能,本節將設計復雜程度不同的多條機動軌跡,并在三子樣條件下,對基于對偶四元數的導航算法和基于旋轉矢量的傳統導航算法的性能進行對比研究。為了更直觀地驗證采用對偶四元數對于減弱不可交換誤差以提高導航精度的作用,這里暫不考慮算法中基于重力模型計算的重力分量對導航解算結果的影響。因此,在本節的仿真實驗中,將重力加速度近似為常值進行測試。
(1)單軸姿態機動
在載體進行單軸姿態機動時,每次僅繞俯仰軸、偏航軸和滾轉軸中的一個軸,按照一定的角速度變化規律持續做周期運動,姿態角也隨之作周期性的變化,且在規定的時間內達到設定幅值θ。在單軸姿態機動(簡稱軌跡1)下,單周期的基本軌跡參數如表1所示,按照該參數共持續25個周期,總運行時間為1000s,導航解算周期為0.03s。
表2列出了載體分別繞俯仰軸、偏航軸與滾轉軸做姿態機動,當θ分別為30°、60°和80°時的導航解算誤差結果。由于純捷聯慣導算法的解算誤差是隨著時間累積而增大的,故表2中數據統計的是終點時刻的導航參數誤差。圖2~圖4所示為當俯仰角變化幅值為30°時,兩種解算方法的導航誤差曲線。圖中紅線為對偶四元數導航算法的解算結果,藍線為傳統三子樣算法的解算結果。
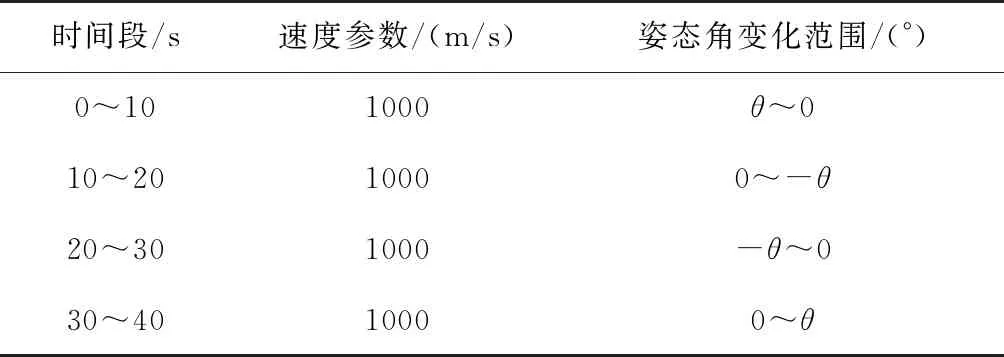
表1 軌跡1參數說明
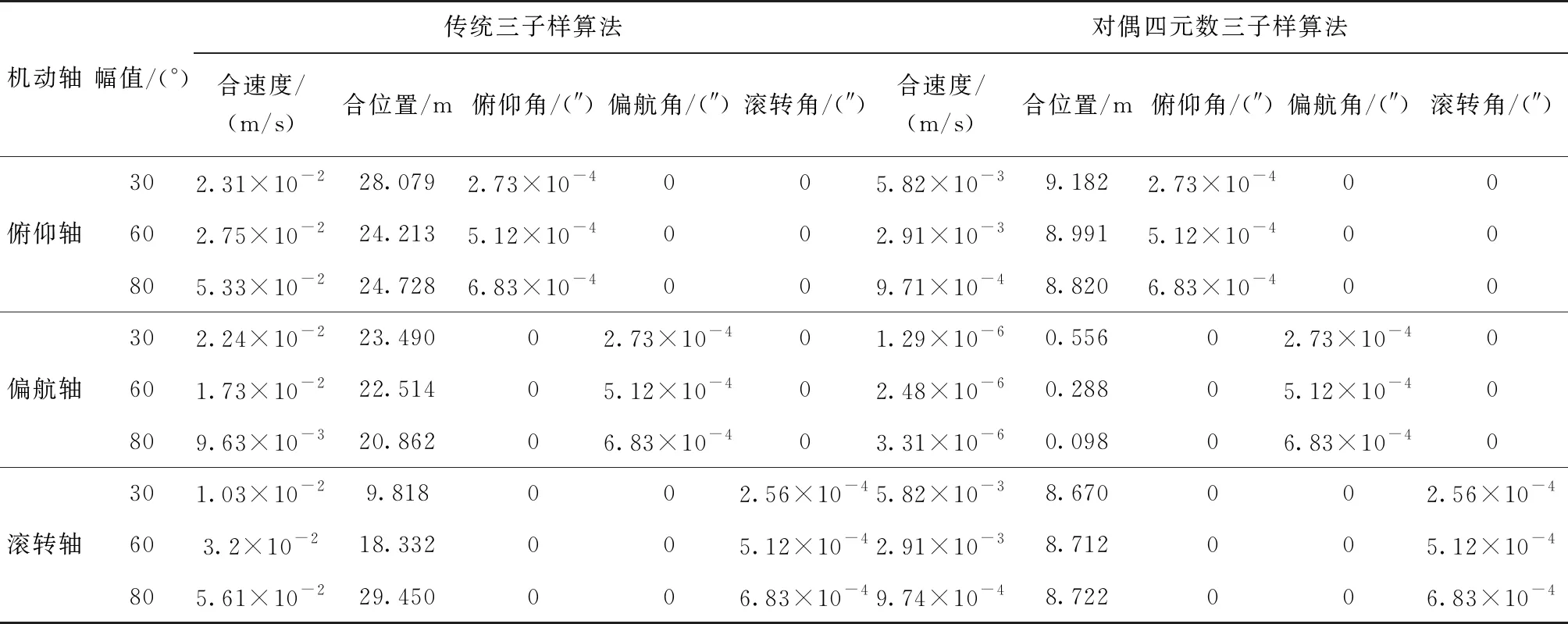
表2 載體單軸機動時導航誤差
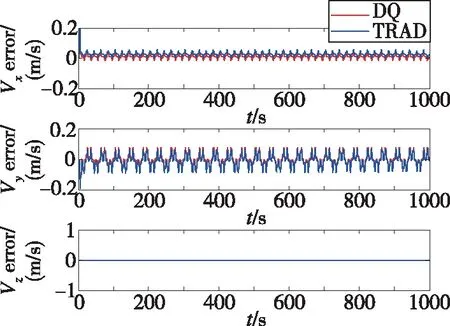
圖2 速度誤差(軌跡1)Fig.2 Velocity error(trajectory 1)
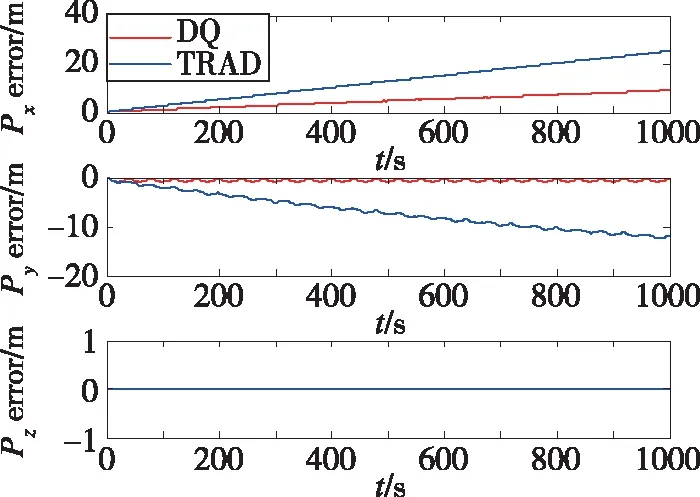
圖3 位置誤差(軌跡1)Fig.3 Position error(trajectory 1)
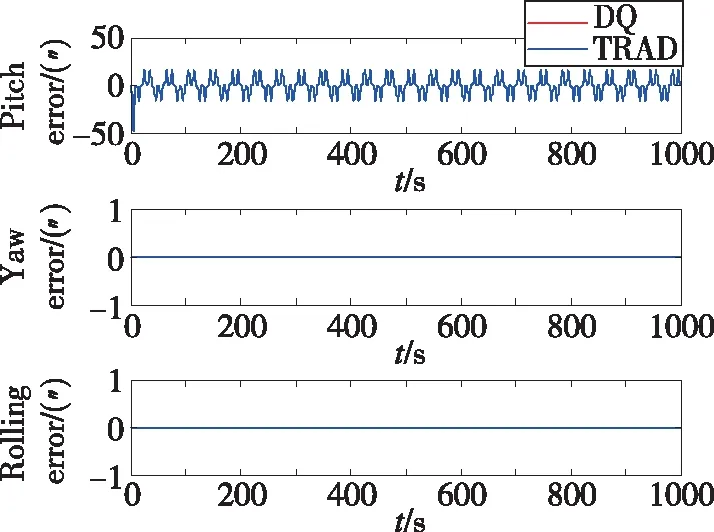
圖4 姿態誤差(軌跡1)Fig.4 Attitude error(trajectory 1)
由表2和圖2、圖3可以看出,使用對偶四元數導航算法解算的速度和位置的精度明顯高于傳統的三子樣算法。其中位置誤差由24m減小到9m左右,速度誤差也減小了很多,這就驗證了第2節的理論分析。從圖4可以看出,兩種方法解算得到的姿態誤差曲線幾乎重合,這說明采用對偶四元數導航算法后,姿態精度并未得到提高,這是因為兩種算法采用的姿態更新原理是一樣的,都是利用對偶四元數的實部即轉動四元數進行姿態的解算。
以上通過單軸姿態機動的仿真實驗,驗證了對偶四元數算法可以有效提高單軸姿態持續機動情況下速度和位置的解算精度,但并不能提高姿態精度。
(2)三軸姿態機動
為了進一步驗證對偶四元數算法在復雜機動情況下的性能,設計了三軸同時進行姿態機動的軌跡,即每次同時繞俯仰軸、偏航軸和滾轉軸按照一定的角速度變化規律持續做周期運動,姿態角也隨之做周期性的變化,且在規定的時間內達到設定幅值θ。在三軸復雜姿態機動(簡稱軌跡2)下,單周期的基本軌跡參數如表3所示,按照該參數共持續25個周期,總運行時間為1000s,導航解算周期為0.03s。
表4列出了載體按照表3中的參數進行三軸姿態機動時的終點導航誤差。圖5~圖7所示為載體按軌跡2機動時,兩種導航解算方法下的導航誤差曲線對比圖。圖中紅線為對偶四元數導航算法的解算結果,藍線為傳統三子樣算法的解算結果。

表3 軌跡2說明

表4 載體三軸姿態機動時導航誤差
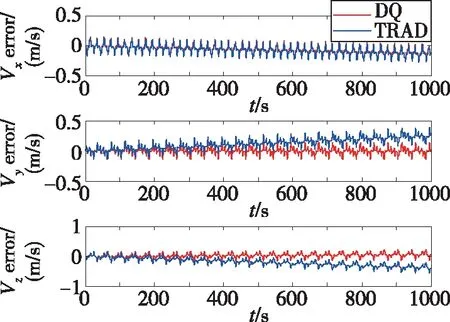
圖5 速度誤差(軌跡2)Fig.5 Velocity error( trajectory 2)

圖6 位置誤差(軌跡2)Fig.6 Position error(trajectory 2)
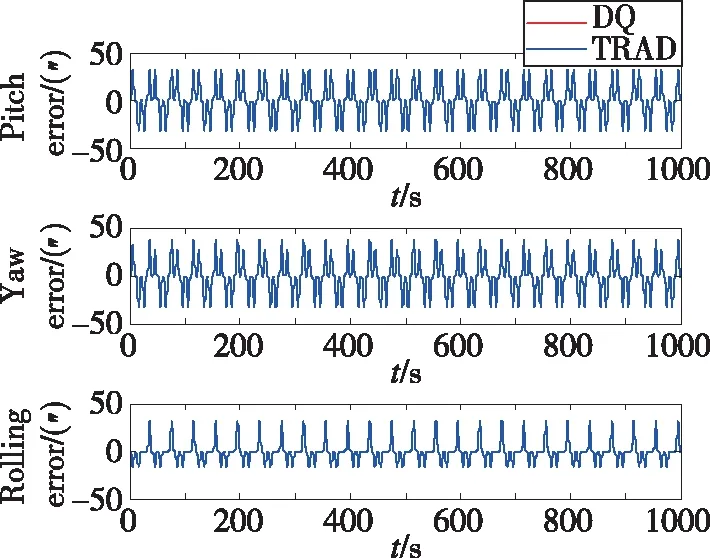
圖7 姿態誤差(軌跡2)Fig.7 Attitude error(trajectory 2)
由圖5和圖6可以看出,對偶四元數算法解算出的三軸速度和位置誤差明顯小于傳統算法的解算結果,其中終點位置誤差由240多m減小到60多m。由此可見,當載體按照軌跡2機動時,采用對偶四元數算法解算的速度和位置精度有顯著提高,且隨著時間的推移和機動復雜性的增加,這種精度優勢更加明顯。
由圖7可以看出,兩種算法下的姿態誤差曲線幾乎重合,這是由于兩種算法中的姿態更新方法無本質區別,因此,對偶四元數導航算法并不能提高姿態的解算精度。
4 結論
本文以發射點慣性系為導航系的彈類載體為對象,針對彈載捷聯慣性導航系統在高動態環境下容易產生圓錐誤差與劃船誤差的問題,設計了基于對偶四元數的捷聯慣性導航算法,并通過仿真實驗驗證了方法的有效性。通過對三子樣下的基于對偶四元數的捷聯慣性導航算法和傳統算法的理論分析與實驗結果對比分析表明:
1)對偶四元數導航算法可以同時補償系統的圓錐誤差與劃船誤差,速度和位置的解算精度明顯高于傳統算法,但姿態精度相當。
2)載體所作的機動越復雜、持續時間越長,基于對偶四元數的捷聯慣導算法的精度優勢越明顯。

