基于帶有事件觸發機制的集員濾波的RSSI室內移動定位

王田田，楊 波

(山西大學數學科學學院，太原 030006)

0 引言

近年來，隨著智能手機和平板電腦等移動智能終端的普及，人們對基于位置服務的需求日益增長。根據《室內外高精度定位導航白皮書》顯示，導航與位置服務在新一代信息技術中具有舉足輕重的地位。調查顯示，人們80%以上的時間處于室內環境中(含地下、礦井、隧道、機場、火車站等)，因此室內位置服務具有廣闊的應用前景[1]。眾所周知，室外環境下，以空中衛星為基礎的全球導航衛星系統(Global Navigation Satellite System，GNSS)被廣泛應用且具有極高的精度。然而在室內環境下，由于衛星信號受到建筑物阻隔，導致GNSS信號快速衰減，使得GNSS無法滿足室內定位需求。為了實現高精度的室內定位，基于超寬帶(Ultra Wide Band，UWB)[2]、 無線射頻識別[3]、WiFi[4]和Zigbee[5]等技術的各種室內定位系統得到了廣泛研究。其中基于接收信號強度指數(Received Signal Strength Indicator,RSSI)的WiFi和Zigbee等技術具有低成本、低功耗、易部署等優勢，使得基于RSSI的室內定位得到了廣泛關注。

基于RSSI的距離測量方法的基本工作原理是利用RSSI值與距離之間存在的關系。根據移動終端測量接收到的信號強度和已知的無線測距模型，可以估算出收發方之間的距離。由于無線電信號在傳輸過程中容易受到環境的干擾，導致測量得到的RSSI值含有測量噪聲，進而影響了定位精度。為了降低外界噪聲對定位結果的影響， 常采用Kalman濾波[6]和粒子濾波等方法估計目標位置，然而這些方法要求知道噪聲的統計特性。在許多實際應用中，噪聲信號多是未知的，但是噪聲的邊界容易獲得，因而可考慮采用集員濾波來處理未知但有界的噪聲[7]，且集員濾波可以提供包含目標真實狀態的集合，使得定位結果更可靠。

自文獻[8]和文獻[9]提出集員濾波后，集員濾波在理論與應用上都引起了很多學者的注意。文獻[10]采用凸優化方法處理范數有界不確定系統的魯棒集員濾波問題。文獻[11]將集員濾波用于移動機器人定位。文獻[12]解決了一類具有傳感器飽和的離散時變系統的集員濾波問題。為了減輕通信負擔，文獻[13]采用事件觸發通信協議處理離散非線性系統的分布式集員濾波問題。最近，文獻[14]在基于RSSI的室內定位問題中采用了集員濾波算法，然而該文獻僅研究了固定點定位問題，而沒有考慮室內環境下移動節點的定位問題。 因此，本文采用集員濾波估計移動節點的位置，可以求出包含目標真實位置的區域，從而得到更可靠的位置估計，并且考慮了事件觸發機制以降低節點的傳輸與計算負擔。

結合集員濾波的特點，本文提出了一種改進的橢圓三邊定位算法，克服了由于RSSI測距誤差導致的三邊定位算法無法獲得可行解的問題，同時針對因目標移動而導致估計誤差增大的問題，提出了一種錨節點自主選擇與切換方法。 最后針對噪聲統計特性未知的情況，考慮了帶有事件觸發機制的集員濾波方法來估計移動目標位置，以提高估計結果的可靠性，同時減少不必要的信息傳輸與計算，節約通信資源，降低能耗。

1 問題描述

本文研究了無線傳感網絡(Wireless Sensor Network, WSN)上基于RSSI的室內移動目標的定位問題。傳感網絡結構如圖1所示，傳感器i可接收來自待測節點的信息，也可接收兩個鄰居節點j和l的測量信息。定位系統的狀態方程可用式(1)描述

xk+1=Akxk+Bkωk+uk

(1)

其中，xk+1∈R2表示系統狀態，也就是移動目標位置；Ak和Bk是維度匹配的已知矩陣；uk是已知的控制輸入；ωk∈R2是未知但有界的過程噪聲，且滿足

(2)

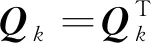
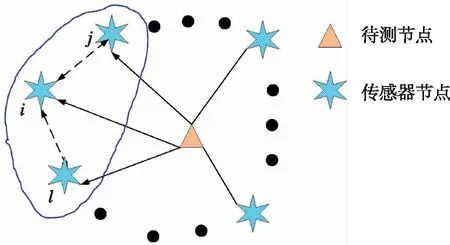
圖1 傳感網絡結構示意圖Fig.1 Structure of WSN

第i個傳感器的測量方程為

(3)

其中，根據文獻[15]有

(4)

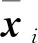
(5)

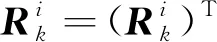
本文首先使用三邊定位算法求解目標位置的初值，然后考慮通過切換傳感器降低由于距離增長RSSI值衰減造成的估計誤差增大的問題，最后采用集員濾波求解出包含目標真實狀態的橢球。

2 三邊定位求初值

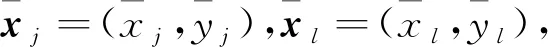
RSSI=A-10γlgd

(6)

式中，A和γ是與環境相關的系數，可通過線性回歸法求得。由此可得

(7)

理想的三邊定位算法是以錨點坐標為圓心、錨點到待測節點的距離為半徑作圓，三個圓交于一點。然而，在實際應用中，由于環境影響，測量值RSSI可能存在誤差，導致出現三個圓不交于一點甚至不相交的情況。針對這一問題，并結合集員濾波的特點，本文提出了一種改進的三邊定位算法來計算集員濾波的初值。 在介紹算法前，先引入需要用到的來自文獻[17]的兩個引理。

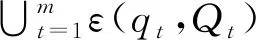
min log detA-1

s.t.λt>0,

t=1,…,m

(8)

然后，根據q=-A-1b,Q=(ATA)-1可以確定ε(q,Q)。

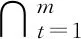
min log detB-1

s.t.λt>0,

(9)

然后，有Q=BTB。

本文提出的改進的三邊定位算法步驟如下：

2)以錨點為圓心、錨點與待測節點之間的距離為半徑作圓，三個圓可分別用式(10)表示

(10)

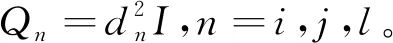
3)用引理1求出三個圓兩兩之間并集的最小外包橢圓，即

(11)

(12)

(13)

4)用引理2求出上一步中三個橢圓交集的體積最大內部橢球，即

(14)

(15)

本文所提的三邊定位算法在三圓交于一點、交于一個區域或不相交的情況下都可以求出包含待測節點真實狀態的橢圓。

3 錨節點切換與選擇機制

隨著目標移動，待測目標節點先接近傳感器節點后逐漸遠離，從而與當前錨節點之間的距離不斷增大，其相應的RSSI值也隨之先增大后衰減，如圖2所示。且根據式(6)可知，隨著距離的增大，RSSI 值對距離的改變也越來越不敏感，從而導致測量誤差增大，因此本文提出了一種根據RSSI值范圍選擇錨節點的方法。以錨節點i為例，RSSI值與目標位置之間的關系為

(16)

從而有

(17)

(18)

圖2 RSSI值變化趨勢Fig.2 Change of RSSI

根據式(6)，可得RSSI對距離d的導數為

(19)

令(RSSI)′<-δ，其中，δ>0為給定閾值，可得

(20)

從而有

(21)

選擇RSSI值滿足式(21)的錨節點作為下一個用于測量的錨節點，從而使RSSI保持在對距離變化足夠敏感的范圍內。

4 基于事件觸發的集員濾波估計位置

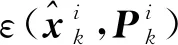
4.1 節點i處的本地估計

(22)

濾波器為

(23)

(24)

其中

(25)

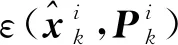
(26)

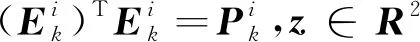
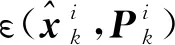
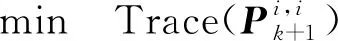
(27)

其中

1)基于微課的自主學習：翻轉課堂順利實施的技術支持就是微課，特別是在實踐性較強的計算機公共類課程中，把微課作為輔助教學非常便利，學生可以不受時間、地點的限制，多次地通過觀看微課進行知識的復習和強化。在具體實現時，根據不同的課程要求，教師構建基于微課的課程自主學習平臺，平臺主要包括以下功能：

(28)

Ξi,i=diag{1-τi,1-τi,2-τi,3,τi,1I,

(29)

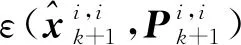
定理1的證明如下：

根據式(22)～式(24)有

(30)

令

(31)

從而有

(32)

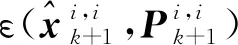
(33)

根據式(32)，式(33)可轉化為

(34)

(35)

(36)

(37)

(38)

式(38)也等價于下面更緊湊的形式

(39)

通過使用文獻[18]的Schur complement引理將式(39)轉換為式(27)，證明完畢。

4.2 基于節點j的更新估計

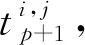
(40)

其中，l為事先設定的觸發閾值。

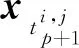
(41)

其中

(42)

(43)

(44)

定理2的證明如下：

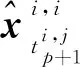
(45)

從而可得

(46)

設

(47)

因此，式(46)可轉化為

φy,jξi,j=0

(48)

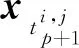
(49)

根據定理1有

(50)

因此可得

(51)

即

(52)

因此，式(49)可轉化為

(53)

(54)

(55)

通過S-Procedure可得式(48)和式(53)～式(55)的等價形式

(56)

式(56)等價于

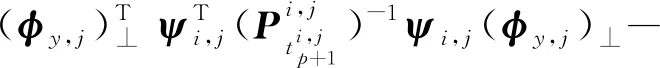
(57)

使用Schur complement引理可將式(57)轉化為式(41)，證畢。

基于鄰居節點l的信息交互估計與基于鄰居節點j的信息交互過程類似，此處省略。

5 仿真驗證

5.1 三邊定位

考慮一個基于RSSI的室內定位系統，其中三個錨點坐標分別為[1,2],[2,1],[2.5,3]，待測節點坐標為[2,2]，三圓相交于一點、相交于一個區域，以及不相交情況下，采用本文所提三邊定位算法求出的結果分別如圖3所示。 圖中藍色細實線圓表示以錨點為圓心、錨點與待測點距離為半徑所作的圓，黑色虛線橢球表示三個圓兩兩之間交集最小的外包橢球，紫紅色粗實線圓表示最后結果。

圖3(a)展示了三個圓不相交的情況下仍然可以獲得可行解，所得橢球的中心點為[1.7256,1.8356]，用橢球中心點與待測節點之間的距離差表示估計誤差，這種情況下所得的估計誤差為0.3199m。 圖3(b)是三圓交于一個區域的情況， 所得橢球的中心點為[1.6236,1.7622]，因此誤差為0.4452m。 圖3(c)是三圓交于一點的情況，求出的橢球中心點為[1.6918,1.8376]，誤差為0.3483m。

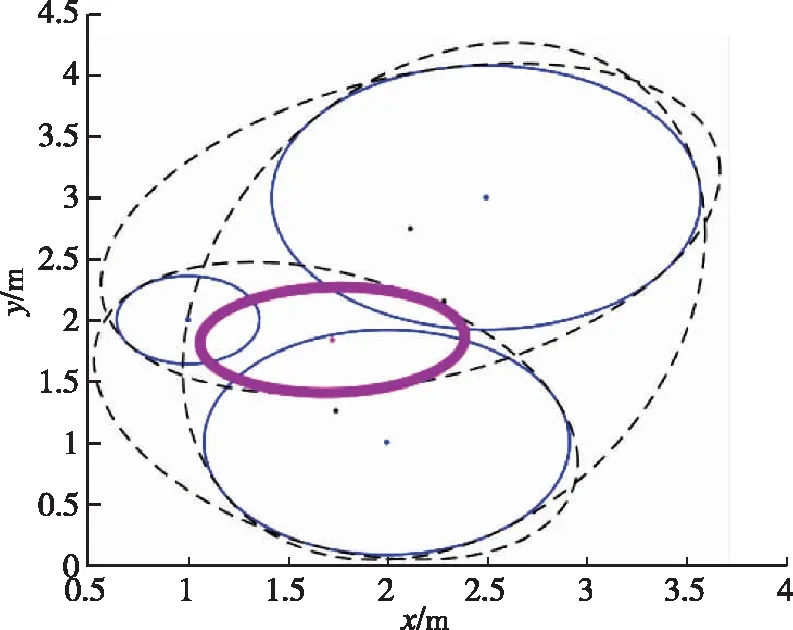
圖3(a) 三圓不相交情況Fig.3(a) Three circles without intersection

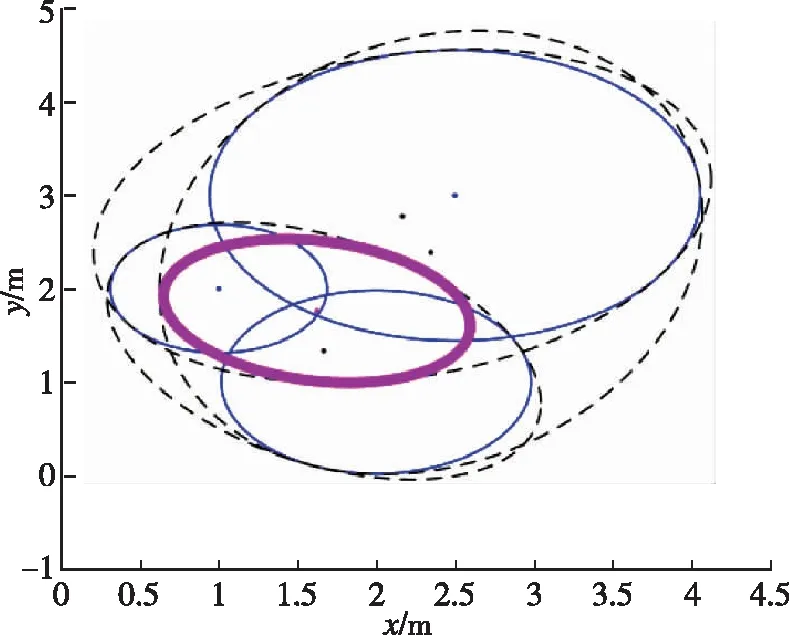
圖3(b) 三圓相交一個區域情況Fig.3(b) Three circles intersect

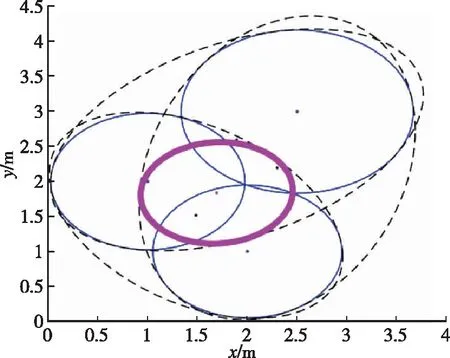
圖3(c) 三圓相交一個點情況Fig.3(c) Three circles intersect at a point

總之，本文所提三邊定位算法在各種情況下都可以求出包含真實狀態的橢球，為之后的集員濾波算法提供了一個良好的基礎。

5.2 集員濾波

考慮一個基于RSSI的室內動態目標跟蹤系統，其狀態方程為

xk+1=xk+ωk+uk

(58)

其中，uk=[0.1,0.1]T是控制輸入；xk=[xk,yk]T是目標位置坐標；過程噪聲ωk=0.05sin(k)。

第i個傳感器的測量方程為

(59)

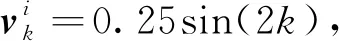
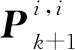
基于上述參數，在不使用錨節點切換方法前，使用本文提出的集員濾波估計目標位置的仿真結果如圖4(a)和4(b)所示，使用錨節點切換后的估計橢球如圖4(c)所示。估計誤差用真實狀態與估計橢球中心之間的距離差來表示。從圖4可以看出，在使用錨節點切換與不使用錨節點切換兩種情況下，目標真實狀態都始終位于估計橢球中。從圖5可以看出，隨著目標逐漸遠離初始傳感器節點，無錨節點切換且只有三個錨節點的情況下橢球尺寸逐漸增大，當使用九個錨節點時，橢球尺寸比無錨節點切換情況下使用三個錨節點時的橢球尺寸小，但計算量大幅增加；而有錨節點切換的情況下，每次只使用三個錨節點的測量值就能使橢球尺寸比使用九個錨節點時小，且基本保持收斂。圖6比較了有無錨節點切換情況下集員濾波算法與擴展Kalman濾波(Extended Kalman Filter, EKF)的誤差。從圖6可以看出，有錨節點切換時估計誤差比其他兩種情況都小，擴展Kalman濾波在噪聲方差精確已知的情況下誤差較小且比較穩定；但是當噪聲方差不精確時誤差比其他情況都大，而在實際中，很難獲得精確的噪聲方差，因此集員濾波算法更有優勢。總體來看，錨節點切換可以以較小的計算成本使估計橢球收斂，且最后估計誤差小于0.1m，因此選擇有錨節點切換的情況更好。

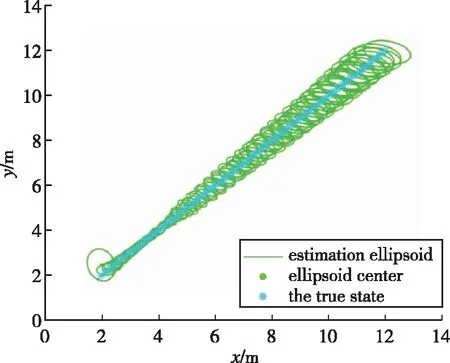
圖4(a) 無錨節點切換時估計結果(三個錨節點)Fig.4(a) Estimation without switch of anchor(three anchors)

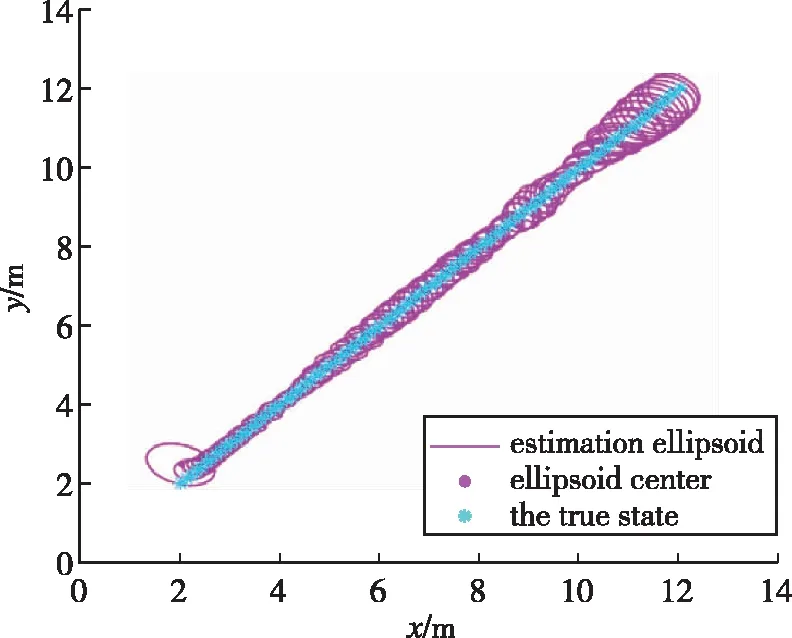
圖4(b) 無錨節點切換時估計結果(九個錨節點)Fig.4(b) Estimation without switch of anchor(nine anchors)

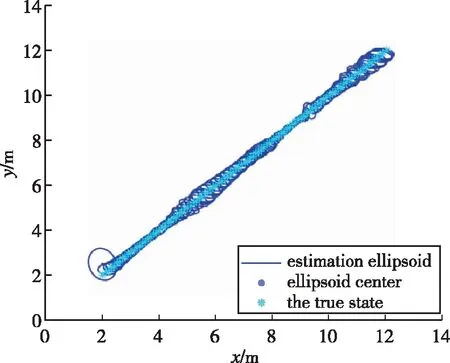
圖4(c) 有錨節點切換時估計結果Fig.4(c) Estimation with switch of anchor

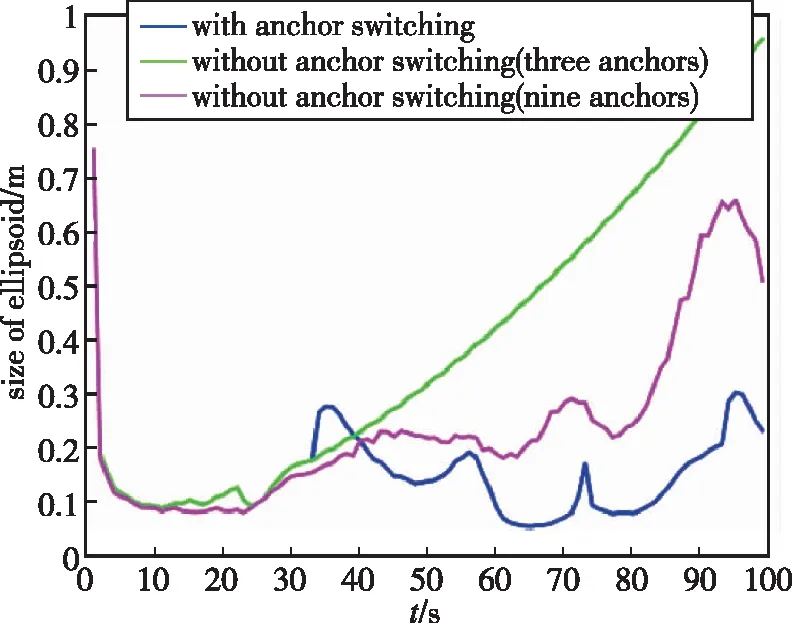
圖5 橢球尺寸Fig.5 Size of ellipsoid

根據式(40)的觸發條件可知，當目標移動較慢或靜止不動時，兩個相鄰時刻的測量值變化幅度不大，可能達不到觸發條件，因此可以降低傳輸頻率。目標節點靜止情況下，從k=1時刻到k=100事件觸發的次數為11，移動情況下觸發次數為92，由此可以得出，靜止時觸發頻率較低，有效降低了傳輸與計算頻率，節約了通信與計算資源。

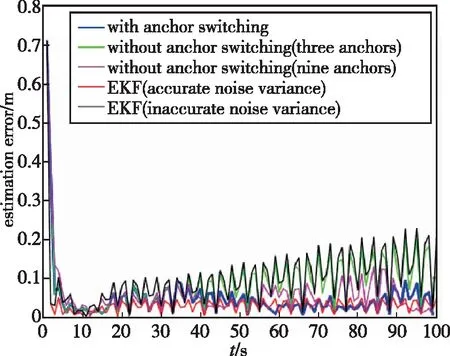
圖6 估計誤差Fig.6 Error of estimation

6 結論

隨著信息技術的發展，室內定位技術在基于位置服務相關的領域都占有舉足輕重的地位，如何以有限的成本提供精確可靠的位置估計仍然是制約其發展的難題。為了提供可靠的位置估計，本文首先對三邊定位算法進行了改進，隨后引入基于事件觸發的集員濾波估計移動目標位置，并針對實驗過程中遇到的估計橢球不收斂問題提出了錨節點自主切換機制。算法分析與實驗結果表明：

1)文中引入計算橢球并集最小外包橢球以及計算橢球交集最大內部橢球的算法改進了三邊定位算法，使其在任何情況下都存在可行解。仿真結果表明，所提的改進的三邊定位算法在傳統三邊定位算法無解的情況下仍可獲得較滿意的結果。

2)本文采用基于事件的集員濾波算法進一步降低了噪聲影響，并提出了一種錨節點選擇機制以克服估計橢球不收斂的問題，使用集員濾波可使定位誤差小于0.1m。

3)事件觸發機制可根據目標移動速度調節節點傳輸與計算頻率，有效節約了傳感網絡的通信與計算資源。