陶瓷顆粒堆積床內的流動特性數值模擬分析
潘效軍,趙雪杉
(南京工程學院 研究生院,江蘇 南京210000)
在陶瓷顆粒催化劑生產工藝中,一般認為常用無序堆積床的流動特性是化工反應器設計及優化的重要依據[1-3]。空隙率作為表征堆積床內氣體流動特性的重要參數,具有重要研究價值。工程應用中無序堆積通道內壁面限制所導致的壁面效應[4]通常會帶來不利影響,呈現為空隙率在壁面附近數值最大,在遠離壁面方向沿徑向振蕩減小,并最終逐漸趨近于堆積結構的平均空隙率。空隙率的這種演化特性加劇了顆粒堆積床內流動特性分布的不均性。另一方面,注意到采用實驗研究堆積床內流動特性極其困難,而隨著智能軟件的迅速發展,使用數值模擬逐漸被承認是一個既便捷又準確的普及方法[5-8]。Cundall P等[9]提出將計算流體力學與離散有限元分析相耦合的CFD-DEM建模方法用于顆粒上,是研究氣固兩相流體特性的重要手段。利用該數值模擬方法,學者們針對不同堆積床做了大量研究工作。如胡映學等[4]通過研究堆積床內光滑/波節壁面結構的流動特性,發現盡管光滑壁面的壁面效應很顯著,但其綜合換熱性能更強;黃文博等[10]模擬研究了反應器內不同堆積高度的壓降情況及誤差,通過對比實驗結果,驗證了模擬結果及方法的有效性;Bai Hua等[11]針對不利于反應效果的低管徑-粒徑比(D/d<4)堆積床,通過模擬壓降并與實驗結果對比,驗證了在低管徑-粒徑比條件下,經驗公式的不適用性;董寶川等[2]通過研究顆粒有/無初速度對空隙率的影響,發現盡管初速度的存在可以減小空隙率,但卻增大了壓降。
本文以減輕陶瓷顆粒無序堆積床壁面效應為目的,運用CFD-DEM耦合的方法,研究不同物料流速對光滑壁面堆積床內流動特性的影響。采用管徑-粒徑比為6.33的陶瓷顆粒固定高度堆積床,在通入空氣流速0.3 m·s-1、0.5 m·s-1、0.8 m·s-1的參數條件下,數值模擬研究空隙率、壓降、壓力、流速、流線在堆積床中的分布規律,結合與常用經驗結果的對比,驗證CFD-DEM耦合方法在研究陶瓷顆粒無序堆積床內流動特性方面的可靠性和先進性,以期對實際生產的設計優化具有一定指導意義。
1 物理模型
將100個顆粒在自身重力作用下從指定高度隨機落入管中,以模擬實際堆積過程。堆積模型如圖1所示,計算通道由三部分組成:進口段①,堆積段②和出口段③。其中,進口段長120 mm,堆積高度30 mm,總長650 mm。
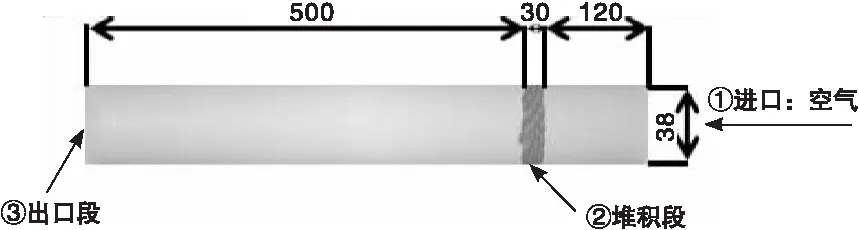
圖1 堆積床物理模型
表1為具體的堆積床模型物性參數。空氣分別以0.3 m·s-1、0.5 m·s-1、0.8 m·s-1的流速從進口段進入,通過堆積段被壁溫加熱后再經出口段流出。室溫(25 ℃)下空氣密度為1.225 kg·m-3,粘度為1.789×10-5Pa·s,對堆積段進行畫網格處理,網格數量約為230萬個。
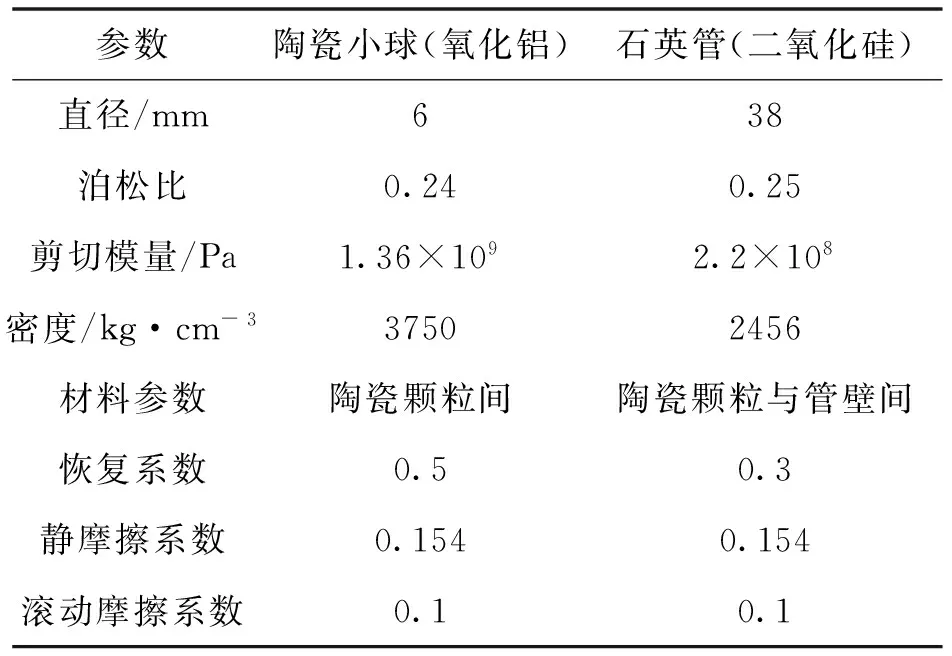
表1 堆積床模型物性參數
2 計算方法及模型驗證
2.1 流動特性影響因素分析
流體通過堆積床需要消耗足夠多的能量,并產生恒定壓降。為減少這種消耗,關注床層壓降非常有必要。影響壓降的因素[6]有:物料流速、空隙率、壁面效應等。在流體力學中,Re是決定流動狀態的重要參數,其具體定義式為:
(公式1)
式中,Us為物料流速;μ為粘度;ρ為密度;L=dh為空隙水力直徑,表示顆粒堆積床中的空隙大小[12],
(公式2)
式中,dp為小球直徑;ε為空隙率。
公式1和公式2中空隙率與雷諾數的關系表明壁面效應對堆積床的影響與雷諾數有關。若雷諾數Re很低,壁面附近流體層流運動,邊界層變厚,相鄰空間中的流體流動受到干擾,壓力損失會隨著墻壁的增加而增加;若雷諾數Re很高,流體湍流運動,邊界層變薄,壁面存在會降低壓降。通過計算得出的是大雷諾數有助于降低床層壓降。因此,有必要研究物料流速、空隙率、壁面效應對堆積床中壓降和流場的影響。
2.2 建模平均空隙率與de Klerk公式對比
管道中的總空隙率由顆粒的數量,填充高度和管道直徑決定。徑向空隙率[13]平行于圓柱管軸產生,定義為:
(公式3)
通過對不同D/d比率的測量和計算,de Klerk[13-14]得出了徑向空隙率的經驗計算公式:
(公式4)
式中,z=(R-r)/d為標準化壁距離;εb為遠壁面空隙率;公式4的第一部分描述了近壁區域的二次下降,而第二部分描述了具有正弦下降函數的徑向空隙率。
利用公式3計算,可得εb=0.66759,并在此條件下,將模擬得出的堆積床徑向空隙率與經驗公式4得出的計算值在保證模擬值和經驗值相對誤差不超過20%的標準下進行模擬方法有效性判定。圖2為兩種方法得出的陶瓷顆粒在遠離壁面不同距離時的空隙率,由圖2可知,陶瓷顆粒在遠壁面時的震蕩趨勢基本一致[15],但在近壁面有所差異,表明模擬結果的連續性能夠彌補de Klerk計算結果的非連續性,CFD-DEM模擬方法準確有效。
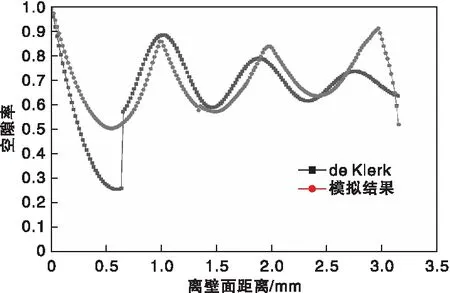
圖2 模擬得到的空隙率與de Klerk計算結果對比
2.3 不同流速下堆積床內的壓降與半經驗公式對比
關于堆積床壓降相關性最熟悉的是Ergun方程[16-17],它由兩項組成,對應于Ergun常數a和b,它們被允許是通用的,且與催化劑顆粒幾何形狀和管尺寸無關。第一項代表了膨脹和收縮對壓降的貢獻,第二項表示阻力對壓降的影響。這個等式的優點是用空隙率充分表征了管堆積,一組廣泛使用Ergun常數來自Handley和Hegg[18],a=150和b=1.75,用于球形顆粒:
(公式5)

圖3 模擬得到的壓降與半經驗公式計算結果對比
由圖3可知,當物料流速在(0.3~0.5)m·s-1時,壓降模擬值與兩個經驗值幾乎重合;在(0.5~0.8)m·s-1時存在誤差,但在允許范圍內,表明CFD-DEM方法準確有效。同時發現,無論流速多大,兩個經驗值幾乎一直重合,驗證了經驗方程的準確性。
3 計算結果分析
圖4為不同物料流速的流線圖。
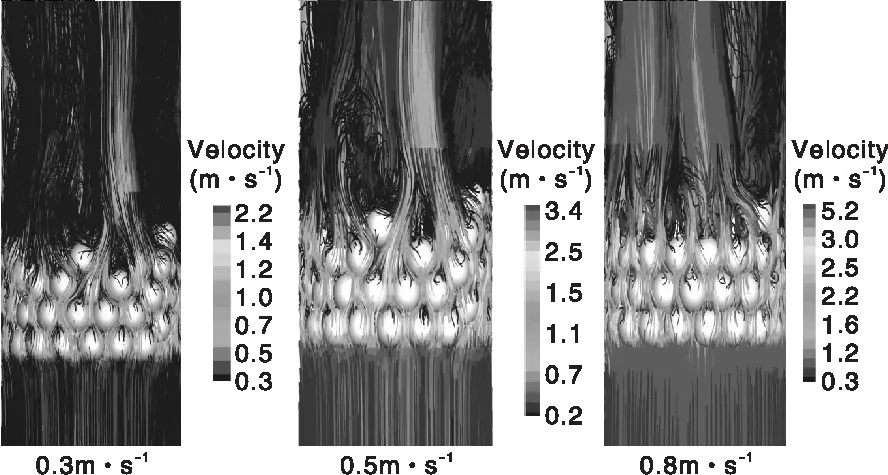
圖4 不同物料流速的流線圖
由圖4可知,空氣流速為0.3 m·s-1、0.5 m·s-1、0.8 m·s-1時,對應的最大速度分別為2.2 m·s-1、3.4 m·s-1、5.2 m·s-1,它們之間的關系式通過牛頓插值法可得:Umax=6US+0.4,表明空氣流速越大,流過顆粒的最大速度越大,流線越密。還發現流速的增加緩和了回流程度;相鄰顆粒之間的通道越窄,速度越大。
圖5為不同物料流速的中心截面速度圖。
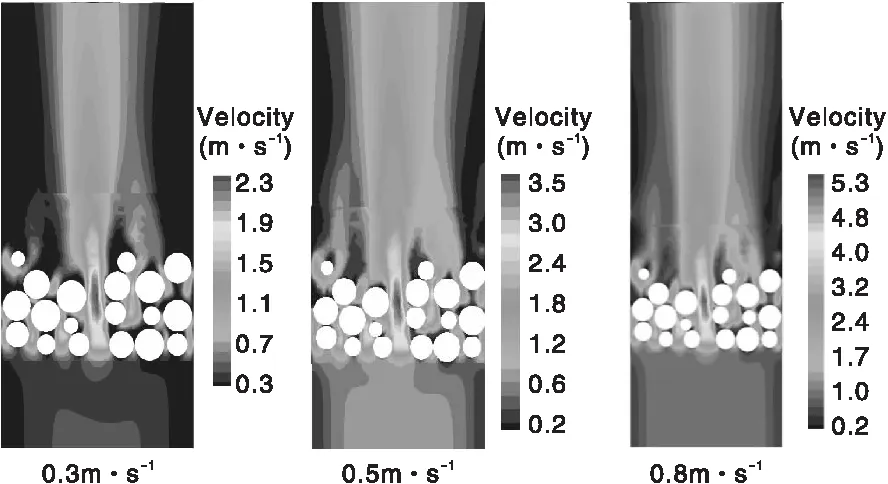
圖5 不同物料流速的中心截面速度圖
由圖5可知,由于壁面效應,中心處空隙率小,流過顆粒的速度大,導致軸向中心處的速度明顯高于其他區域。空氣流速為0.3 m·s-1、0.5 m·s-1、0.8 m·s-1時,中心處的最大速度分別為2.3 m·s-1、3.5 m·s-1、5.3 m·s-1,表明空氣流速越大,中心截面最大速度越大;與流過顆粒的最大速度相比,中心處的最大速度分別增加了4.5%、2.9%、1.9%,說明空氣流速的增加使中心截面最大速速增加的比例變小,中心處顆粒之間的通道相對變寬,空隙率相對變大,減輕了壁面效應對整個堆積床流動的影響。
圖6為不同物料流速的中心截面壓力圖。
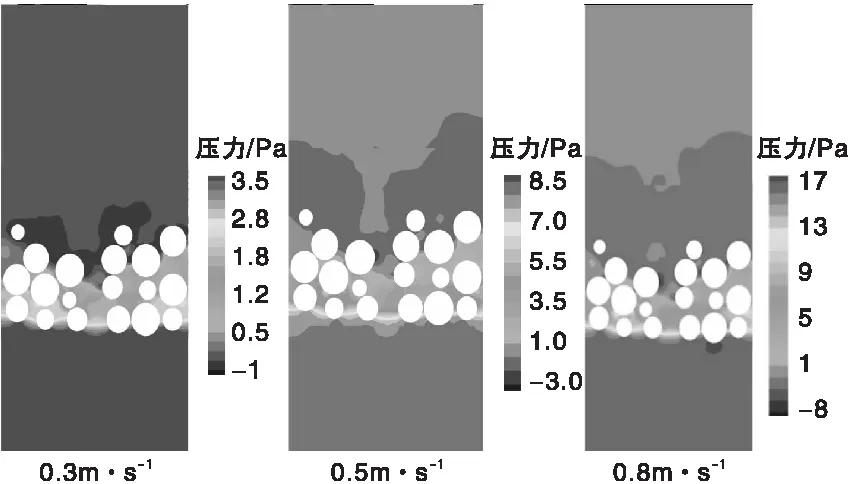
圖6 不同物料流速的中心截面壓力圖
從圖6可以看出,沿堆積床流動方向壓力逐層下降,同時經理論分析注意到,由于壁面效應近壁處的速度低于中間區域的速度,導致近壁壓力高于同一高度的內部壓力,相同堆積高度近壁處的壓降小;隨著空氣流速的增加,入口壓力越來越高,出口壓力越來越低。當空氣流速為0.3 m·s-1、0.5 m·s-1、0.8 m·s-1時,對應的壓降分別為4.50 Pa、11.5 Pa、25.0 Pa,利用牛頓插值法計算它們之間的關系為:ΔH=20US2+19US-3,表明空氣流速的增加使壓降線性增加;從近壁側考慮,壓力為(1.20~2.30)Pa、(2.66~5.50)Pa、(4.50~11.0)Pa,對應的壓降分別為1.10 Pa、2.84 Pa、6.50 Pa,它們與整個堆積床的壓降之比分別為24.4%、24.7%、26.0%,表明空氣流速的增加使近壁壓降增長率變大,近壁空隙率相對變小;從中心處考慮,壓力為(-1.00~2.05)Pa、(-1.70~5.50)Pa、(-3.50~10.0)Pa,對應的壓降分別為3.05 Pa、7.20 Pa、13.5 Pa,它們與整個堆積床的壓降之比分別為67.8%、62.6%、54.0%,表明空氣流速的增加導致中心處壓降增長率變小,中心處空隙率相對變大;對中心處和近壁處的壓降增長率加權平均,結果為46.1%、43.7%、40.0%。因此,在實際設計優化中,同等條件下選擇物料流速較大的方案能有效改善壁面效應,但流速過大導致的壓降過大反而會引起操作困難,動力消耗大、顆粒和堆積床容易受損等問題。
4 結 論
采用離散元素法(DEM)和計算流體動力學(CFD)耦合以模擬大管徑-粒徑比(D/d=6.33)堆積床的流場分布,主要結論如下:
(1)在適當的物料流速和耦合模型條件下,CFD-DEM方法誤差小于期望的極限(20%),能取得與常用經驗方法較為接近的結果,良好一致地驗證了模型。另一方面,CFD-DEM 方法不僅能預測堆積床的壓降,還能反映整個堆積床內壓力、空隙率、速度的分布情況,對堆積床的設計和優化具體一定的指導意義。
(2)通過對管道通入流速分別為0.3 m·s-1、0.5 m·s-1、0.8 m·s-1的空氣,分析壁面效應與物料流速、壓降、空隙率之間的關系,結果表明采用流速為0.8 m·s-1的空氣可以減小壁面效應的影響。在實際工業設計中,優化堆積床反應器可以從這一點考慮,但過大的流速會造成操作困難,顆粒和床層受損,增大能源消耗等一系列不利因素。因此,要根據實際情況選擇合適的物料流速。
(3)利用牛頓插值法進行壓降,流速的線性擬合具有計算簡便,增加節點時只增加一項的優點。

