基于理解，走向豐富

錢蔚

教材是教學的依據，是實現教學目標的重要載體。理解教材是教師有效教學的前提，是提高教學質量的關鍵。“角的初步認識”是蘇教版小學數學教材二年級下冊的教學內容，由于角的抽象性，低年級學生不容易建立數學角的幾何表象。如何幫助學生有效建立數學角的幾何表象呢？又如何根據低年級學生的認知規律設計有效活動，幫助他們建立由模糊到清晰、從直觀到抽象的角的認識呢？我們基于理解，進行了教學改進與思考。

一、補充圖示，豐富概念

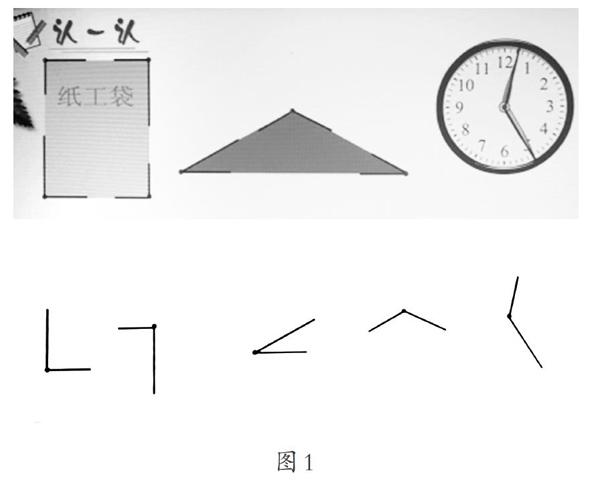
數學與生活緊密相連，教材例1通過兩個學生做手工的情境，呈現表面有角的物體，并分別從三角尺、紙工袋、鐘面指針抽象出銳角、直角、鈍角。教材如此安排是“用心良苦”的，這三個角具有代表性，分別代表了三類角，它們都具有角的特征，含有角這個概念的一般屬性。第一次試教，教師依照教材進行教學設計，再請學生找出物體上的角并抽象出三個角后，讓學生觀察并概括角有什么共同特征。學生不僅說出了教師需要的答案：角有兩條線是直的，兩條線都靠在一起;還說出了教師意想不到的答案：角的開口都是朝同一個方向的。但是，對學生而言，僅有三個角的視覺表征是不夠的。要正確理解角，還要讓學生觀察大大小小的、不同方向的，還有一些邊看起來不一樣長的角，從而讓學生在觀察中經歷分析、排除、概括的思維過程，抽取出角的本質屬性。于是，我們在教學設計時稍做改變，仍然采用教材主題圖，在學生指出三種物體表面的各個角后，有選擇性地抽象出了部分不同的角（如圖1）。

教材設計有時受版面等因素的限制，圖示有限，教師要站在學生的視角，在教學設計中補充圖示，豐富概念。如此，更有利于學生理解概念的本質。

二、動態比較，拓寬概念

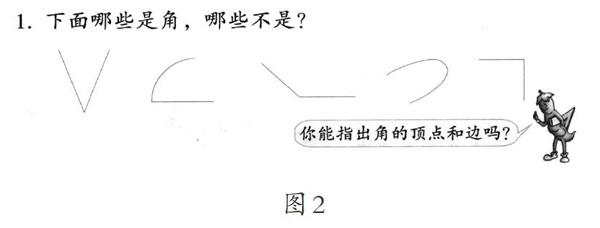
概念習得要善于利用正例，也要善于利用反例。在“角的初步認識”中，教材編者安排了角的判斷練習（如圖2），為進一步感知數學角的概念起到了很好的作用。教學中，教師讓學生說出判斷結論的理由，學生表達流暢。但是，我們總感覺這樣的設計缺少對角的內涵的滲透與拓展。經過進一步學習理解，我們從角的靜態定義和動態定義得到啟發：能否將該練習在動態中進行呢？于是，我們利用多媒體進行了改進。

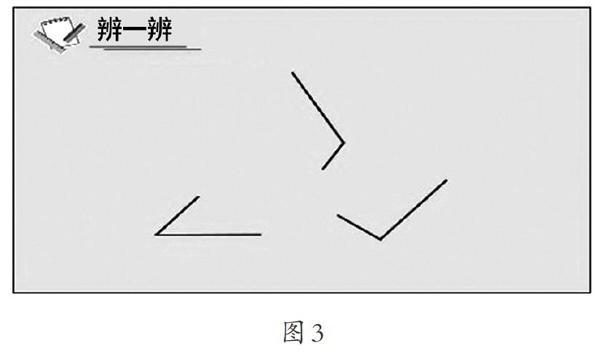
課件動態演示：在黑屏狀態下，屏幕上出現一個亮點，從這一點出發，依次出現兩條射線，形成開口方向、大小以及兩邊長短不同的角，讓學生辨析。當屏幕上出現一個角的兩條邊長短不同時（如圖3，為了圖的清晰，去除了黑屏），學生開始爭辯起來。

生：這不是角，因為一條邊長，另一條邊短。

生：我覺得還是一個角，因為它有一個頂點和兩條邊，而且角的兩條邊不一定要一樣長。

師：真好！這個圖形確實仍然是一個角，它是由一個頂點和兩條邊組成的。

教師利用課件依次呈現下面的兩個圖形（如圖4，如圖5）。

師：這兩個圖形也是角嗎？

生：不是。

師：為什么？

生：圖4中的圖形一條邊是直的，另一條邊是彎的，而角的兩條邊都應該是直的。

生：圖5中的圖形沒有頂點，也沒有兩條直直的邊。

師：確實如此，我們判斷一個圖形是不是角，就要緊緊抓住角的特點。角的特點是什么？

生（齊）：都有一個頂點和兩條邊。

這一教學環節的設計體現了“高立意，低起點”的教學思想。教師變靜態的圖形判斷為動態形成圖形之后的判斷，充分體現了角的本質特征。教學中，教師運用多媒體手段，在黑屏狀態下用亮點和線分別呈現不同的圖形，讓學生通過對角的變式圖形以及正反例的辨析，進一步豐富角的表象，加深對角的特點的認識。

三、分層比較，積累經驗

在例1后面，教材安排了試一試（如圖6）。通過活動角，學生體驗角是有大小的，并會比較角的大小。教學過程中，教師提供活動角，學生在角的變大變小中玩得不亦樂乎，“角是有大小的”“兩邊張開角變大、兩邊合攏角變小”。教師對“比較角的大小”教學進行了反思：通過活動角感受“角是有大小的”，既符合低段學生的認知特點，也符合角的本質特征。如何使學生對角的大小有更深的體驗呢？我們在原先設計的基礎上進行了分層設計，力圖加深學生對角的大小體驗，積累數學活動經驗。

（一）比較活動角的大小

師：既然角是有大小的，我們就來比一比角的大小。拿出你的活動角，要讓這個角變大一些，怎么辦？

（學生紛紛把手中的活動角的兩條邊張開一些）

師：要讓你手中的活動角變小一些呢？

（學生紛紛把手中的活動角的兩條邊合攏一些）

師：要讓你手中的活動角變得和同桌的一樣大，怎么辦？

（學生操作后演示：兩個活動角頂點與頂點重合，兩條邊也分別重合）

師：能把你手上的活動角變得和老師這個角一樣大嗎？

（學生操作后演示：活動角的頂點與三角尺上一個角的頂點重合，活動角的兩條邊分別與三角尺上這個角的兩條邊重合）

師：你還能把手上的活動角變得比這個角更大一些嗎？

（學生繼續演示：讓活動角的頂點與老師手中的一個角的頂點重合，一條邊與這個角的一條邊重合，另一條邊往外再張開一些）

師（小結）：比較活動角大小，我們只要頂點對頂點，一條邊對一條邊，看另一條邊在哪里就能比較了。

（二）比較靜態角的大小

師：同學們，大家剛才畫出的角也是有大有小的。你也能比一比嗎？實物展臺呈現學生畫的兩個大小不同的角（如圖7）。

師：看一看，知道哪個角大嗎？

生：②號角大。

師：你是怎樣看出來的？

生：②號角的兩條邊張開大。

師：是的，角的兩條邊張開得越大，這個角也就越大。下面的兩個角呢？

實物展臺呈現圖8：

學生意見不統一，有人說③號角大，有人說④號角大，有人說兩個角大小相等。

師：意見不統一，怎么辦？能利用我們手中的活動角解決問題嗎？和你的同桌商量一下。

（學生分組討論后，繼續交流）

生：可以用兩個活動角分別比一比（邊說邊在實物展臺上演示），先讓一個活動角和③號角一樣大，再讓另一個活動角和④號角一樣大，最后比較兩個活動角的大小。

生：用一個活動角也能比出它們的大小（邊說邊在實物展臺上演示），先使活動角和③號角一樣大，再用活動角和④號角比一比。

師：你用活動角把這個角搬下來，保持不動，再和另一個角比一比！這個辦法更簡單了。

學生理解“感受角的大小與兩條邊張開的大小有關”有一定困難。為此，教學中，教師分兩個層次來幫助學生體驗、理解。首先，教師為每個學生準備了活動角，讓學生在活動中初步體會角的大小與兩條邊張開的程度有關。然后引導學生按要求制作活動角，把自己所做的活動角“變大一些”“變小一些”“變得和老師的一樣大”，使他們進一步明確：角的兩條邊張開得越大，角就越大;角的兩條邊張開得越小，角就越小。其次，教師從學生處得到啟發，設計了請學生比較兩組角（靜態角）的大小的活動，幫助他們在鞏固對角的大小的認識的同時，進一步體會解決問題方法的多樣化，積累了解決問題的經驗，發展了數學思維。

（作者單位：江蘇省無錫市查橋實驗小學）