基于改進FI-NN 算法的時域超前變槳控制

秦佳暉, 曾憲文, 高桂革

(上海電機學院a.電子信息學院;b.電氣學院, 上海201306)

隨著我國風電技術的發展,風電的單機容量越來越大,更大的轉動慣性和遲滯的系統響應為傳統的變槳控制方式帶來了挑戰。對此,國內外學者對風速模型和變槳控制系統進行了廣泛的研究。文獻[1-2]分別使用了神經網絡和模糊控制作為變槳前饋控制部分,改善了機組系統滯后。文獻[3]利用卡爾曼濾波器設計了一種前饋變槳控制方法,改善了機組系統時滯。文獻[4]結合差分算法和粒子群優化算法,減少了變槳進入穩定狀態的時間。文獻[5]結合多種不同的模糊結構和滑模控制,使變槳模型適用于不同工況。文獻[6]設計了一種部分離線型的模糊PI前饋變槳控制器,減輕了在線模糊PI前饋變槳控制的計算負擔。文獻[7]在BP神經網絡預測變槳的基礎上加入了參數預處理。文獻[8-10]以粒子群優化算法為主,混合了多種不同算法,取得了良好的改進效果。

雖然不同機器學習算法的組合可以改進變槳控制系統的性能,但是組合算法必須在更好的控制性能與引入更多的機器學習類算法固有缺點之間進行取舍[11]。分形插值是一種針對非線性對象的計算方法,其常被用于股市曲線預測,非常符合風速的變化特征[12-14]。本文改進了經典分形插值—神經網絡預測(Fractal Interpolation-Neural Network,FI-NN),并基于改進FI-NN提出了一種時域超前變槳控制方法。仿真驗證了FI-NN預測對變槳控制性能的提高,同時分形插值是一種非機器學習算法,不會引入更多機器學習算法的固有缺點,如易陷入局部最優和需要大量訓練樣本。

1 分形插值函數與風電變槳原理

1.1 分形插值函數

分形是一門研究幾何圖形自相似性的學科,分形插值使用了迭代函數系統(Iteration Function System,IFS)進行插值,所以分形插值是一種非線性圖形的插值方法。IFS通過構建迭代方程得到插值點:

式中:ωi(x j)和ωi(y j)分別為第i個IFS系統中第j個分形插值點的橫坐標和縱坐標;X j和Y j分別為待插值曲線中第j個離散數據點的橫坐標和縱坐標;d i為自由變量,決定IFS在映射過程中的垂直比例縮放,又稱為垂直比例因子;a i、e i、c i、f i均為IFS中的中間參數,其值為

式中:X i、Y i、X i+1、Y i+1分別為待插值曲線第i和i+1組離散數據的橫坐標和縱坐標;X0、Y0分別為待插值曲線起始離散數據的橫坐標和縱坐標;X N、Y N分別為待插值曲線末尾離散數據的橫坐標和縱坐標。

1.2 變槳控制原理

當雙饋異步風力發電機(Doubly Fed Induction Generator,DFIG)功率輸出超過額定功率時,需要通過增大槳距角從而降低風輪吸收的功率。風輪吸收功率為

式中:ρ為空氣密度;R為葉片半徑;v為風速;Cp為風能利用系數;λ為葉尖速比;β為槳距角(增大槳距角可使Cp變小,從而降低葉輪吸收的功率[15])。

圖1 風速數據的EMD分解結果

2 基于改進FI-NN的風速預測

2.1 風速分形插值理論依據

通過對某實驗室的風速數據進行經驗模態分解(Empirical Mode Decomposition,EMD)和希爾伯特變換(Hilbert Transform,HT),發現不同采樣頻率風速數據分頻分量之間存在著比例關系,如圖1所示。圖1中橫坐標是以小時為采樣周期的風速數據中的頻率分量,縱坐標是以分鐘為采樣周期的風速數據中的頻率分量。兩者組成的坐標可以近似地擬合成一條直線,說明不同采樣頻率風速在頻率上具有分形的特點,而分形插值則可以通過低采樣頻率數據預測出高采樣頻率數據。

2.2 改進的FI-NN風速預測算法

改進的FI-NN 風速預測算法流程如圖2所示。圖2中虛線框部分為改進部分。經典FI-NN中的d i采用隨機變量,使分形得到的曲線垂直尺度縮放存在誤差。本文通過分析得到歷史d i變化曲線,然后利用神經網絡對d i進行預測,從而提高FI-NN的預測精度。

預測算法的總體步驟可以分為以下3 步:①利用梯度下降法得到歷史d i曲線;②通過神__經網絡對未來d i與大致風速走向進行預測;③利用分形插值得到風速預測數據。

圖2 風速預測流程

為了確定d i的歷史變化曲線,本文利用梯度向量法分析歷史d i變化過程,以線性相關系數作為梯度下降法中的損失函數,有________________

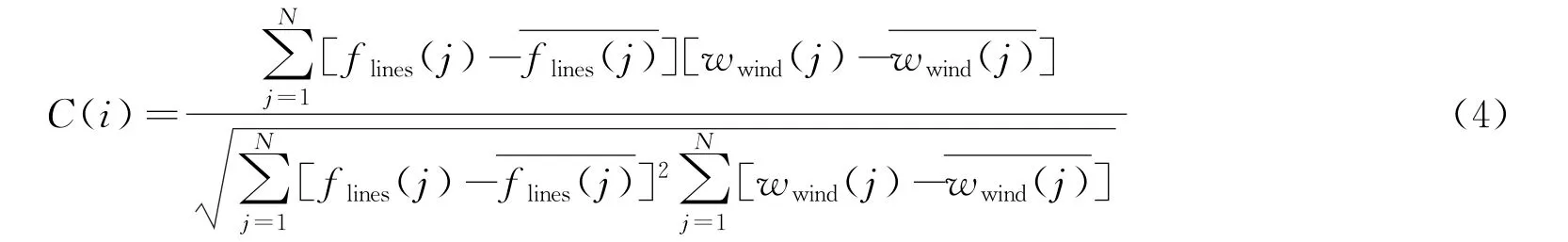
式中:i為分形區間段序號;C(i)為線性相關系數;flines(j)為分形插值得到的擬合曲線;wwind(j)為實際歷史風速曲線;j為一個分形區間段內的離散數據序號;N為總的離散數據個數。

根據下式更新得到歷史d i變化數據為(式中d i表達為d(i))

式中:Lr為梯度速率。

2.3 改進FI-NN的風速預測仿真

利用歷史風速數據和d i數據訓練BP神經網絡并預測,得到大范圍內的低頻風速與d i的未來趨向;再將BP神經網絡預測數據重新分形插值,得到高精度風速預測數據。仿真得到的4月11日前140 min,以1 min為離散間隔的風速預測結果對比,如圖3所示。圖3中,實線為本文經過d i分析改良的FI-NN 分形插值預測曲線,虛線為實際風速曲線,帶點虛線為傳統隨機d i的FI-NN 預測曲線。可以看到,本文的方法有效減少了預測誤差。神經網絡訓練數據均來自于某實驗室4月4日～10日的風速離散數據。

圖3 風速預測圖

3 基于改進FI-NN的變槳控制

3.1 風速前饋控制

前饋控制可以消除系統響應遲滯,快速變槳。對DFIG的前饋功率控制有

式中:Pwaste為從葉輪吸收功率到風力發電機輸出功率之間的功率耗損,其值一般在2%到5%之間,本文為2.5%;Pgen為DFIG穩態輸出功率。

求解式(6)即可得到Pgen和v下的前饋β值。

3.2 基于改進FI-NN的時域超前變槳控制

式(6)中v為實時風速,本文將v改為預測風速,實現了時域超前變槳控制。時域超前變槳控制的流程如圖4所示。

圖4中,v、Pgen、DFIG 轉速、ρ和R為輸入參數,預測β值為輸出參數。DFIG功率控制方程模塊利用式(6)和輸入參數求解,在預測風速條件下,能夠將DFIG的Pgen穩定在額定功率的β值。求解得到的β值與前饋控制下的β值相比,在時域上呈現超前特性,故稱為時域超前變槳控制。在時域超前變槳控制中,通過計算v得到的β值將被直接發送給變槳執行機構,從而在風速變化到來前提前變槳。

圖4 時域超前變槳控制流程

經典變速變槳可以做到在協同控制區內對Pgen曲線削峰填谷。但當DFIG轉子軸轉速ωgen達到最大值時,轉子會因為無法吸收更多的動能而無法削去Pgen曲線多余的峰值,這時對Pgen曲線的控制就需要盡量避免出現波峰。這種情況下時域超前變槳的特性便優于經典變速變槳。雖然轉子無法通過吸收更多的動能削去Pgen曲線多余的峰值,但是仍可以提取儲存于轉子中的動能補充Pgen曲線的低谷。時域超前變槳可以做到在ωgen超速前主動降速,避免因前饋控制而產生的ωgen和Pgen雙超調情況。

具體的Pgen控制改進過程如圖5所示。圖5中,標注序號為①、②、③的曲線分別為改進前的Pgen曲線、時域超前變槳后的Pgen曲線和最終經過轉子動能補償的Pgen曲線。DFIG 首先通過時域超前變槳消除變槳機構在時滯上的影響和Pgen上的超調波峰,并提前使β達到預測風速工作點。此時曲線①被調整為曲線②,然后通過提取轉子中的動能彌補時域超前變槳帶來的波谷,有效避免了ωgen陷入因控制不及時而產生的超速,此時曲線②被調整為曲線③。

圖5 預測控制下的功率超調改善

3.3 雙模控制切換判據

經典變速變槳控制可以儲存轉子動能,穩定Pgen曲線,時域超前變槳控制可以避免ωgen超速和Pgen超調。兩種控制方法之間切換的判據,一是預測風速高于實時風速,該情況下未來風輪功率會猛增,從而導致ωgen可能產生超調;二是判斷預測風速增長帶來的Pgen增長是否會引起ωgen超速。如果風輪吸收的Pgen增長會使得ωgen超速,那么預測周期內的齒輪箱增速量一定大于前一時刻轉速與額定轉速的轉速差,即齒輪箱增速率在風速預測時間周期內的積分存在不等式關系,即

式中:ΔPwind為實時前饋控制下的功率偏差;Prate為DFIG額定功率;k為齒輪箱傳動比;ΔTpre為預測點離散間隔;ωrate為額定轉速;ωt為風輪轉速;Jg為DFIG轉動慣量;Jwind為風輪轉動慣量。

當兩個條件都滿足時,說明風速所引起的轉速增量大于轉速裕度,經典變速變槳控制切換為時域超前變槳控制,避免轉速超速。

4 基于改進FI-NN的時域超前變槳控制仿真

仿真對象為建立在Simulink平臺上的額定功率2 MW 的DFIG。變槳采用了一階慣性環節模擬變槳產生的遲滯,控制模型輸入為2.3節得到的預測風速,DFIG 的初始狀態為:ωgen=250 rad/s,ωrate=250 rad/s,Prate=2 MW,變槳指令由3.2節中時域超前變槳控制系統給出。經典變速變槳控制和時域超前變槳控制在ωgen臨界點附近運行時的各項輸出對比如圖6所示。

圖6中,虛線為前饋控制下的變速變槳階段DFIG各項輸出曲線,實線為加入了時域超前變槳預測控制的DFIG各項輸出參數曲線。從圖6(a)和圖6(d)可以看到,當預測到風速猛增可能導致ωgen和Pgen超調時,預測控制進行了時域超前變槳。從圖6(b)中可以看到,預測控制在時域超前變槳時使得ωgen得到了下降,有效限制了ωgen超速。圖6(c)顯示出預測控制消除了前饋控制因變槳跟蹤誤差所產生的Pgen誤差。仿真顯示,即便預測風速具有一定的偏差,預測控制仍然在消除ωgen和Pgen的超調上表現良好。

圖6 前饋控制與預測控制對比

5 結 語

本文的主要工作內容和創新點包括:①利用EMD分解和HT 變換對分形插值和風速預測的結合進行了理論分析;②結合d i分析和神經網絡改進了經典FI-NN算法;③基于改進FI-NN算法提出了時域超前變槳控制方法,并通過Matlab仿真驗證了該方法對穩定DFIG輸出功率的作用。