基于變結構多模型的SINS/DVL組合導航算法

李 倩，王健成，尹冬寒，臧新樂，奔粵陽，趙玉新

(1.哈爾濱工程大學智能科學與工程學院，哈爾濱 150001；2.中國船舶工業集團公司第七○八研究所，上海 201100)

0 引言

捷聯慣性導航系統(Strapdown Inertial Navigation System, SINS)是一種自主式導航系統，被認為是水下導航領域中最可靠的導航系統，在短時間內具有較高的導航精度。但是由于陀螺漂移和加速度計零偏的存在， 導致其誤差不斷積累，因此無法長時間單獨工作。對于水下環境，由于全球定位系統(Global Positioning System，GPS)信號會迅速衰減[1-3]，因此常用多普勒計程儀(Doppler Velocity Log, DVL)輔助SINS為無人水下航行器提供精確的導航信息[4]。DVL有兩種工作模式：底跟蹤模式和水跟蹤模式。DVL一般工作在底跟蹤模式，將DVL提供的相對地面的速度與SINS融合，為載體提供精確的導航信息。然而，DVL受作用深度限制，在超過一定范圍時，DVL將工作在水跟蹤模式下，此時DVL只能為載體提供相對于水的速度。若將相對于水的速度作為相對地面的速度信息提供給卡爾曼濾波器(Kalman Filter, KF)對SINS的系統誤差進行估計，此時洋流速度會成為DVL的測量誤差，將導致SINS / DVL組合導航性能降低，甚至導航失敗[5-7]。

為了提高SINS/DVL組合導航系統的性能，文獻[8]提出了一種解決方案，將洋流速度建模為常數，考慮其對系統的影響，并將其增廣到KF的狀態量中， 基于長基線/超短基線(Long Baseline/Ultra-short Baseline， LBL/USBL)和DVL提供的位置和速度信息，采用KF估計洋流速度。文獻[9]采用模型輔助慣性導航系統對自主水下航行器(Autono-mous Underwater Vehicle, AUV)導航解算方法進行改進，該模型可以在線估計洋流速度參數,但需要提供精確的AUV動態模型以及外部定位信息。以上方法均需一些外部定位信息，而對于水下環境，連續的外部位置信息有時難以獲得。此外，簡單地將洋流速度建模為常數以補償DVL水跟蹤模式下的測量誤差，在短時間內有一定的效果，但不適用于長航時和廣海域環境。為了進一步降低洋流常值模型對SINS/DVL組合導航系統造成的影響，文獻[10]使用一階馬爾可夫過程來描述洋流速度的變化，并通過KF實時估算洋流速度，從而校正系統誤差。在很多情況下，一階馬爾可夫過程洋流速度模型中的相關時間常數會隨著季節、位置、鹽度和天氣條件等外部因素的變化而變化[11-12]。因此，單一的洋流速度模型往往無法表征其流速變化。

針對洋流速度模型的不確定性，文獻[13]利用交互式多模型(Interactive Multiple Model, IMM)算法估計洋流速度，以減小其對導航精度的影響。在該算法中，兩個KF在不同的洋流速度模型下并行運行，然后進行輸出融合，得到洋流速度的估計值。然而，在實際應用中，僅僅建立一個由兩個洋流速度模型組成的小模型群是不夠的。為了提高估計效果就要使用較大的模型群，這樣就會增大計算量，難以滿足導航系統的實時性要求[14]。同時，某些不必要的模型間會存在過度競爭的問題，而在狀態估計過程中利用太多的模型也會降低算法的性能[15]。

利用IMM算法進行組合導航時，一方面要保證模型群有足夠多的模型來覆蓋系統的實際模型；另一方面，為了保證計算速度，需要盡量使用較小的模型數量。顯然，這兩個要求是矛盾的。針對這一問題，1992年，X.Li和Y. Bar-Shalom提出了一種變結構多模型(Variable Structure Multiple Model, VSMM)方法[16-17]。在本文中，采用有向圖切換的變結構多模型(Digraph Switching-Variable Structure Multiple Model, DS-VSMM)算法來實時估計洋流速度。基于有向圖切換方法，設置洋流速度模型群，利用所設置的模型群切換策略對模型群進行激活和終止，使用較少的模型數量實現了洋流速度的準確估計，進而消除了其對SINS/DVL組合導航的影響[18]。

1 SINS/DVL組合導航系統模型建立

SINS/DVL組合導航系統誤差狀態方程為

(1)

式中，狀態變量X為14維列向量；狀態矩陣F為14×14維矩陣；系統噪聲輸入矩陣G和系統噪聲矩陣W為14維列向量。

X=[δLδλδvEδvNφxφyφz

ΔAxΔAyεEεNεUθCEθCN]T

(2)

式中，δL、δλ分別為緯度和經度誤差；δvE、δvN分別為東向和北向速度誤差；φx、φy、φz為平臺失準角；ΔAx、ΔAy分別為東向和北向加速度計零位偏移；εE、εN、εU分別為東向、北向和天向陀螺漂移；θCE、θCN分別為洋流的東向和北向速度。本文主要對洋流速度進行模型群建模，故此處只給出洋流狀態矩陣塊Fon，其余將省略。

(3)

式中，βE、βN分別為東向和北向洋流模型的時間常數。

W=[0 0 0 0 0 0 0ωdEωdNωgE

ωgNωgUωEωN]T

(4)

式中，W為零均值的高斯白噪聲，它的協方差矩陣為Q；ωdE、ωdN分別為加速度計東向和北向噪聲；ωgE、ωgN、ωgU分別為陀螺東向、北向和天向噪聲；ωE、ωN分別為洋流速度模型對應的東向和北向白噪聲。

在水下環境中，如果DVL工作在水跟蹤模式下，則其測得的是對水的相對速度，即

(5)

式中，vE、vN分別為慣導系統計算的東向和北向速度；vDVL(E)、vDVL(N)分別為DVL測得的相對于水的東向和北向速度，對式(5)整理可得

(6)

本文利用慣導解算的速度與DVL測得的速度之差作為濾波器的量測量，則SINS/DVL組合導航系統的量測方程為

(7)

式中，量測噪聲V為零均值白噪聲，它的協方差矩陣為R，式(7)中量測矩陣H為

H=

(8)

2 SINS/DVL組合導航系統模型群的建立

基于DS-VSMM算法對導航參數進行估計，首先建立系統的模型群。根據第1節，洋流速度模型設置為一階馬爾可夫過程，然而在實際中，洋流速度模型中的一階馬爾科夫過程相關時間常數是未知的，它會隨著外部因素的變化而變化。因此，為了能夠準確地估計洋流的速度，在可能的范圍內設置一個大的洋流速度模型群(不同模型對應不同的相關時間常數)。此外，由于水下環境復雜，SINS/DVL組合導航系統中量測噪聲的統計特性也會隨機變化，因此量測噪聲協方差矩陣R也是一個未知的參數。

本文基于不同的相關時間常數β和量測噪聲協方差矩陣R，設置了13個模型。根據式(3)，洋流速度模型相關時間常數β對應狀態轉移矩陣塊Fon，各個模型中對應的狀態矩陣塊Fon和量測噪聲方差矩陣R設置如表1所示。

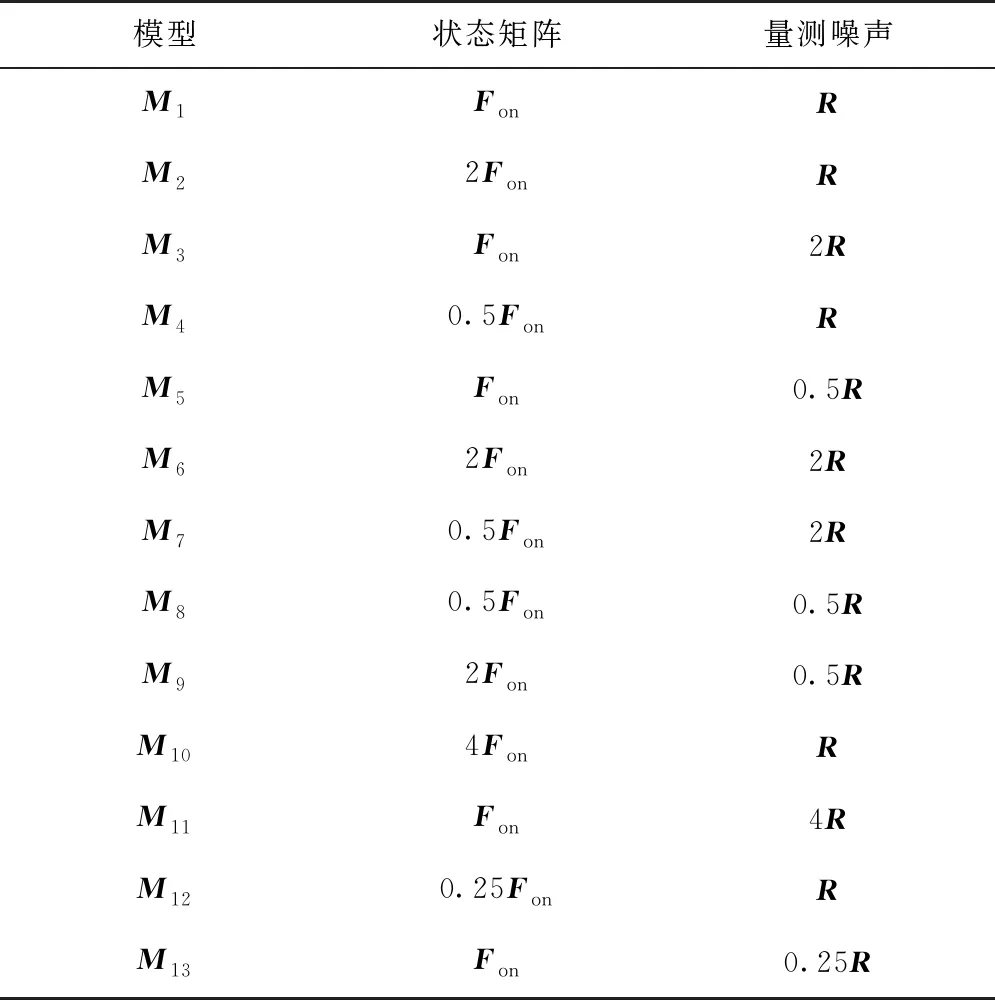
表1 各個模型與洋流模型狀態矩陣塊、量測噪聲方差矩陣的對應關系

假設系統模型的跳變不會出現斷層式的情況，即只在相鄰模型之間切換。例如：系統不會出現從Fon直接越過2Fon跳變到4Fon的情況，R的跳變情況同上，那么SINS/DVL組合導航系統模型跳變的拓撲有向圖如圖1所示。

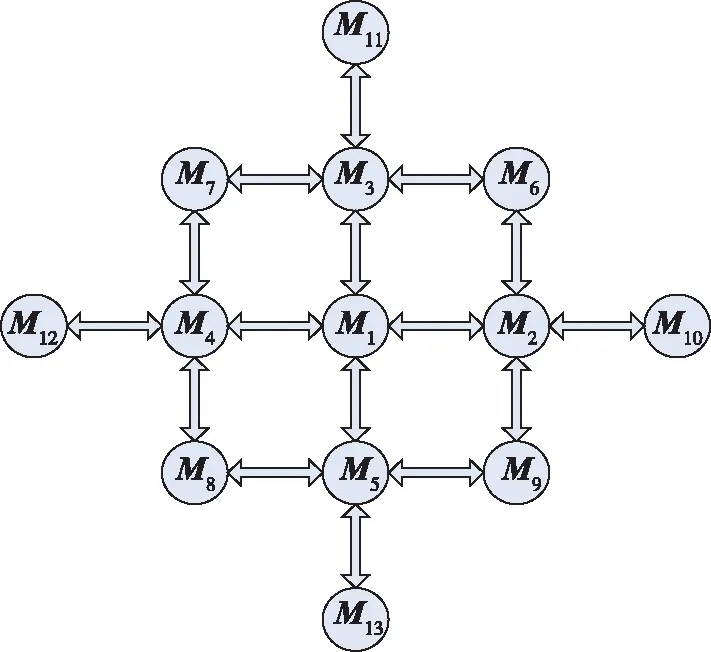
圖1 SINS/DVL組合導航系統整體模型群的有向圖

圖1中，箭頭所指兩個模型可以互相進行切換。將SINS/DVL組合導航系統可能出現的跳變分為四種類型:β變大的跳變、β變小的跳變、R變大的跳變和R變小的跳變。

假設系統當前時刻處于模型M1，隨后可能向模型M2跳變(β增大)，也可能向模型M4跳變(β減小)，也可能向模型M3跳變(R增大)，也可能向模型M5跳變(R減小)，這種情況對應的子模型群為A1={M1,M2,M3,M4,M5}，M1為子模型群A1的中心模型。子模型群A1的有向圖如圖2所示。

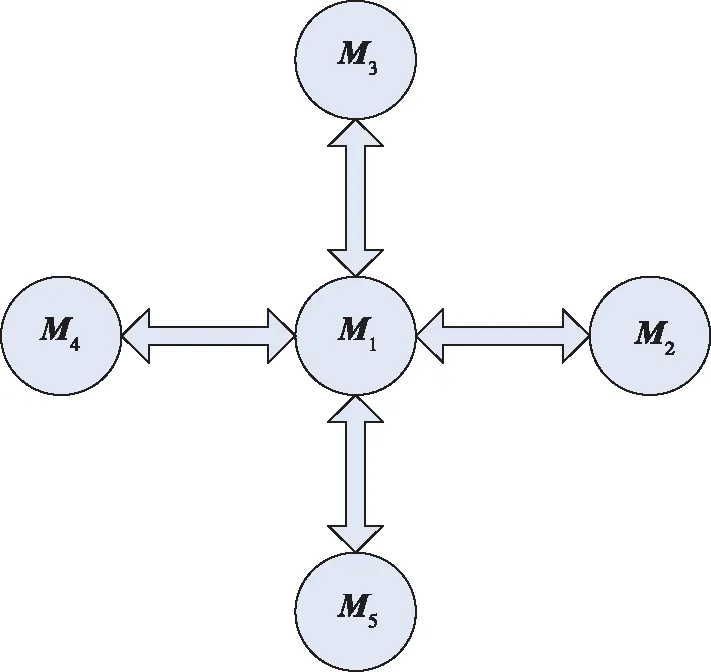
圖2 SINS/DVL組合導航系統子模型群A1的有向圖

與圖2所示的子模型群A1類似，還有分別以M2、M3、M4和M5為中心的子模型群A2、A3、A4和A5

A2={M2,M10,M6,M1,M9}A3={M3,M11,M7,M1,M6}A4={M4,M12,M8,M1,M7}A5={M5,M13,M9,M1,M8}

3 模型群切換算法

模型群切換(Model-GroupSwitching,MGS)算法首先需要設置模型群，隨后要制定MGS算法的自適應策略。MGS算法在運行過程中一般分為兩部分：模型群激活與終止，最后在匹配的有向圖內進行IMM濾波。MGS算法步驟如下：

步驟1：將計數時間k增加1，即k→k+1。運行VSMM[Mk,Mk-1]一個周期。

步驟2：檢測是否有候選模型群被激活。當滿足以下概率條件時

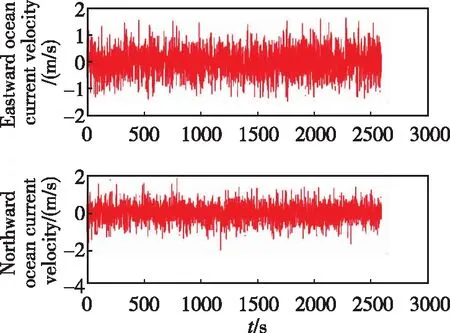
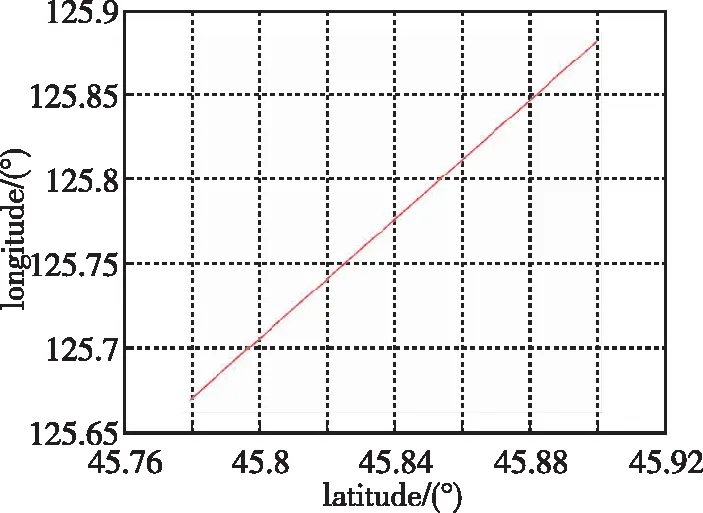
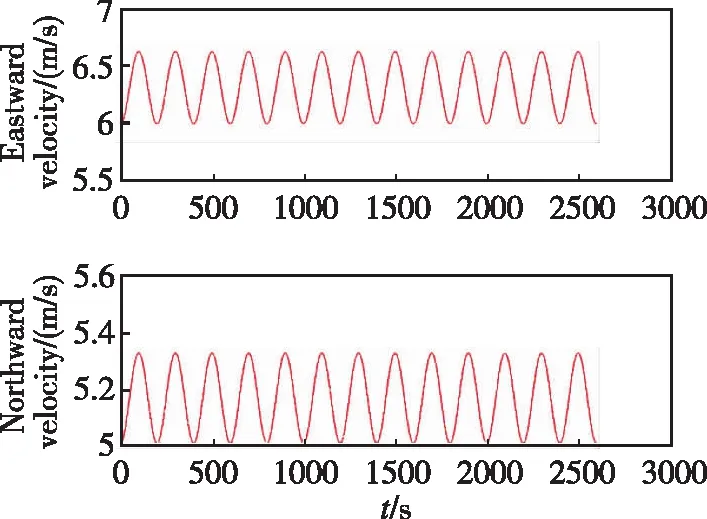
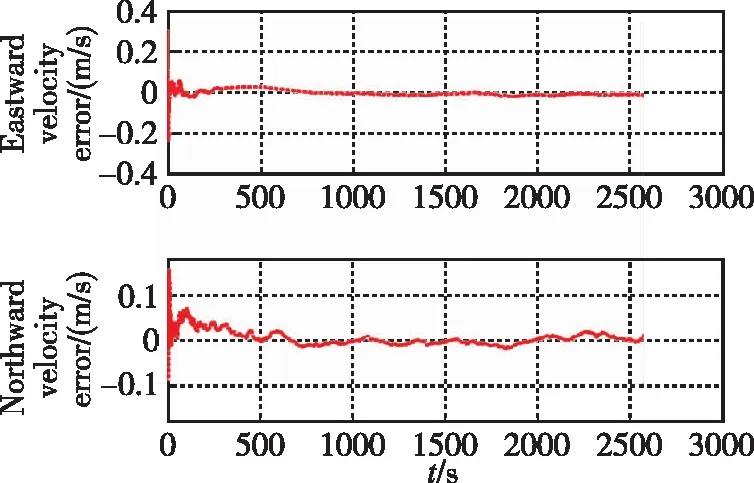
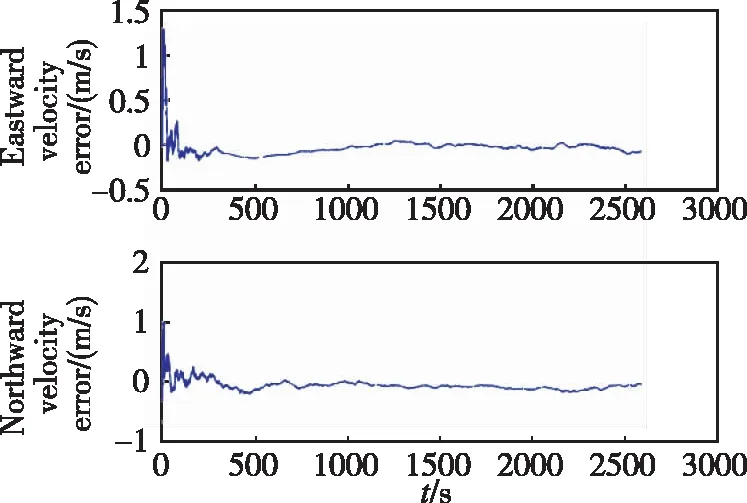
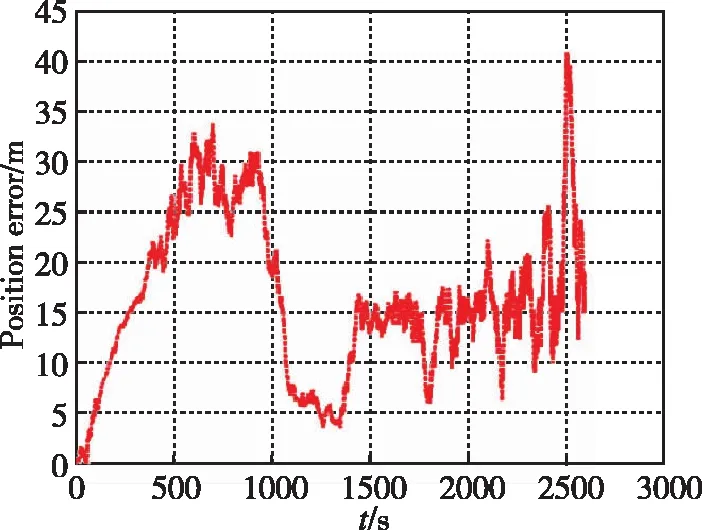
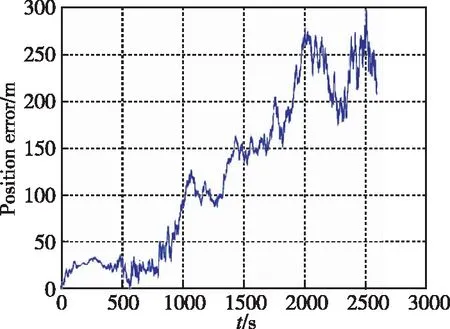
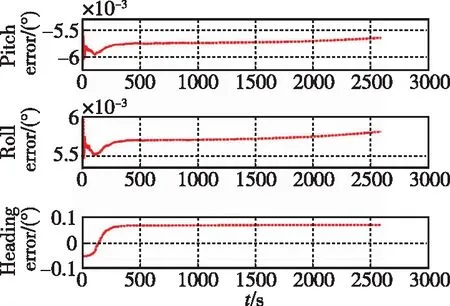
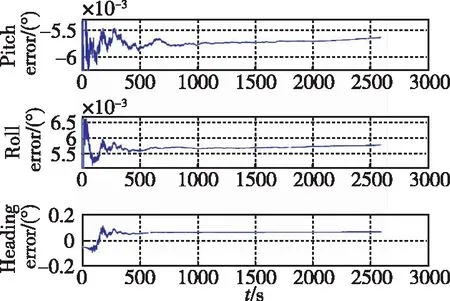
μk

(9)

步驟3：如果模型群Ma被激活，則令Mo=Mk，同時進行如下運算：

1)運行VSMM[Mn,Mk-1]一個周期，其中Mn=Ma-Mo是新模型的集合。

2)令Mk=Mn∪Mo=Ma∪Mo。

3)估計融合：對模型群Mk計算模式概率、狀態估計以及誤差的協方差矩陣，分別如式(10)～式(12)所示

(10)

(11)

(12)

步驟5：模型群Ml=Mo或Ml=Ma，則有式(13)～式(15)

(13)

(14)

(15)

當式(16)或式(17)成立時

(16)

(17)

則終止模型群Ma，令Mk+1=Mo，然后跳轉到步驟1。

當式(18)與式(19)同時成立時

(18)

(19)

則終止模型群Mo，并令Mk+1=Ma，然后跳轉到步驟1。

步驟6：將計數時間k增加1，即k→k+1，同時令Mk+1=Mk，運行VSMM[Mk,Mk-1]一個周期，然后跳轉到步驟4。

4 仿真驗證

為了驗證基于DS-VSMM的SINS/DVL組合導航算法的性能，在仿真環境相同的情況下，對比DS-VSMM算法與IMM算法。

(20)

根據式(20)以及表1，仿真中真實的洋流速度曲線如圖3所示。

圖3 真實的洋流速度曲線圖

此外，這里還給出了仿真環境中設置的載體運動軌跡以及速度變化圖，如圖4和圖5所示。

圖4 載體運動軌跡

圖5 載體的速度變化曲線圖

根據上述仿真環境，分別應用DS-VSMM算法和IMM算法，最終得到兩種算法在SINS/DVL組合導航系統中的誤差，仿真結果如圖6～圖11所示。

圖6 DS-VSMM速度誤差曲線圖

圖7 IMM速度誤差曲線圖

圖8 DS-VSMM位置誤差曲線圖

圖9 IMM位置誤差曲線圖

圖10 DS-VSMM姿態角誤差曲線圖

圖11 IMM姿態角誤差曲線圖

由上述仿真結果曲線對比可知，在橫滾以及俯仰角誤差方面，應用DS-VSMM算法與IMM算法二者無明顯差別；在速度誤差、位置誤差和航向角誤差方面，應用DS-VSMM算法明顯優于IMM算法。綜上所述，本文設計的基于DS-VSMM的SINS/DVL組合導航算法可以更好地消除洋流速度對系統的影響，進一步提高了組合導航系統的性能。

兩種算法運行10次的時間均值如表2所示，表明本文提出的算法具有更優的費效比。

表2 兩種算法運行10次的時間均值對比

IMM算法每次濾波要使用全部13個子模型濾波，而DS-VSMM算法每次濾波只需要使用相應的5個子模型濾波。DS-VSMM算法運行時間理論上是IMM算法運行時間的38.5%，但由于需要進行子模型群切換，進而增加了一定的運行時間，因此根據表2，DS-VSMM算法最終的運行時間是IMM算法的65.4%。綜上所述，基于DS-VSMM算法的SINS/DVL組合導航與應用IMM算法相比，降低了計算量，且進一步提高了系統的性能。

5 結論

本文針對無人水下航行器面臨的不確定性洋流速度影響SINS/DVL組合導航系統導航精度的問題，提出了一種基于DS-VSMM的組合導航算法。當工作在水跟蹤模式下，DVL只能提供相對于水的速度信息，因此洋流速度會影響SINS/DVL組合導航系統的性能。為了能夠準確地對洋流速度進行估計，本文基于有向圖切換方法，建立了洋流速度模型群，通過所設置的模型群切換策略對模型群進行激活和終止，最終實現了對洋流速度的準確估計，進而消除了其對SINS/DVL組合導航系統的影響。仿真結果表明：基于DS-VSMM的SINS/DVL組合導航算法的位置誤差控制在50m之內，而IMM算法的位置誤差接近300m，前者的定位精度明顯優于后者。本文提出的算法可以很好地克服多變的洋流速度引起的導航誤差，同時減少了一定的計算量，提高了效費比，也提高了導航系統的精度，為進一步實現水下高精度SINS/DVL組合導航提供了參考。為進一步提高SINS/DVL組合導航系統的穩定性及水下高精度導航能力，還需要更深入的研究：

1)本文提出的算法構建的洋流速度模型較少，在實際應用中，可以根據具體的導航精度要求設置更多的洋流速度模型；

2)本文的濾波方法為KF，并未進行非線性近似，可使用其他非線性濾波方法進行同條件仿真，比較不同濾波方法的優劣，從而選出最優的濾波算法。