基于自抗擾的無人機(jī)俯仰姿態(tài)控制

蔣玉新，王 平，劉 貝，林祺凱

(海鷹航空通用裝備有限責(zé)任公司，北京 100074)

0 引言

為了高效地完成飛行任務(wù)，無人機(jī)飛行控制系統(tǒng)需要具備良好的性能。姿態(tài)控制回路是飛行控制系統(tǒng)的基礎(chǔ)，其性能直接影響飛行控制系統(tǒng)的品質(zhì)。飛機(jī)在進(jìn)行快速高度機(jī)動(dòng)時(shí)，對俯仰姿態(tài)控制器的動(dòng)態(tài)品質(zhì)提出了較高的要求。此外，在控制系統(tǒng)設(shè)計(jì)過程中，還要面對由于氣動(dòng)參數(shù)攝動(dòng)、傳感器誤差帶來的模型不確定性以及外界環(huán)境的不確定干擾(如大氣紊流)等，在增加設(shè)計(jì)難度的同時(shí)也對飛控系統(tǒng)的魯棒性提出了更高的要求。

目前，工程實(shí)踐中主要基于飛機(jī)小擾動(dòng)線性化模型進(jìn)行多狀態(tài)點(diǎn)PID姿態(tài)控制器設(shè)計(jì)，然而基于該方法所設(shè)計(jì)的控制器在本質(zhì)上只具有在平衡點(diǎn)鄰域內(nèi)的局部穩(wěn)定性[1-2]，還需要在飛行包線內(nèi)選取盡可能多的狀態(tài)點(diǎn)進(jìn)行全包絡(luò)設(shè)計(jì)，增加了控制器設(shè)計(jì)的工作量。

近年來，一種最大程度保持PID 控制形式，同時(shí)借助于現(xiàn)代控制理論中觀測器思想，而不依賴于被控對象模型的自抗擾控制(Active Disturbance Rejection Control, ADRC)方法[3-5]，已在姿態(tài)控制問題上得到了成功應(yīng)用[6-7]。

本文針對固定翼無人機(jī)俯仰姿態(tài)控制回路在模型參數(shù)和復(fù)雜外界環(huán)境等不確定性干擾影響下魯棒性差、系統(tǒng)響應(yīng)速度慢的問題，通過構(gòu)造線性擴(kuò)張狀態(tài)觀測器(Linear Extended Statement Observer, LESO)觀測不確定擾動(dòng)狀態(tài)并在控制回路中反饋補(bǔ)償，使其被快速抑制[8-9]。仿真結(jié)果表明，設(shè)計(jì)的俯仰姿態(tài)控制系統(tǒng)具有較好的性能，能夠?qū)崿F(xiàn)姿態(tài)控制與穩(wěn)定，且提升了系統(tǒng)的魯棒性。

1 無人機(jī)俯仰姿態(tài)控制模型

根據(jù)文獻(xiàn)[10]，無人機(jī)在非大角度縱向機(jī)動(dòng)條件下，六自由度運(yùn)動(dòng)的全狀態(tài)非線性運(yùn)動(dòng)方程如下

(1)

其中，各狀態(tài)參數(shù)依次為：飛機(jī)質(zhì)量m；飛行速度V；發(fā)動(dòng)機(jī)推力P；阻力X；升力Y；側(cè)向力Z；航跡傾角θ；航跡偏角ψv；航跡滾轉(zhuǎn)角γv；攻角α；側(cè)滑角β；橫滾角速度ωx；偏航角速度ωy；俯仰角速度ωz；橫滾角γ；偏航角ψ；俯仰角?；Jx、Jy、Jz分別為飛機(jī)相對于機(jī)體坐標(biāo)系各軸的轉(zhuǎn)動(dòng)慣量；Mx、My、Mz分別為作用在飛機(jī)上的所有外力( 含推力) 對質(zhì)心的力矩在機(jī)體坐標(biāo)系各軸上的分量。

通過變換式(1)中的第6個(gè)等式，得到如下繞軸角加速度方程

(2)

俯仰力矩與升降舵偏的關(guān)系可用如下方程描述

(3)

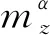
將式(3)代入式(2)，可得

(4)

由式(1)可得

(5)

將式(4)代入式(5)，可得

(6)

2 ADRC設(shè)計(jì)

2.1 LESO設(shè)計(jì)

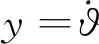
(Jy-Jx)ωyωxcosγ/Jz+

(7)

定義

x1=y

QSLcosγ/Jz-(Jy-Jx)·ωyωxcosγ/Jz+

(8)

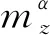
(9)

把式(9)表示成如下矩陣形式

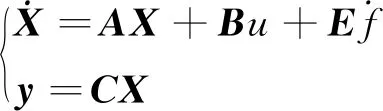
(10)

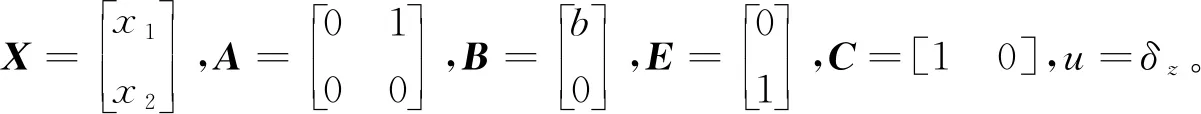
可構(gòu)造系統(tǒng)(10)的觀測器如式(11)所示

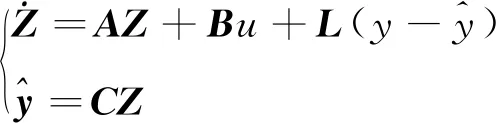
(11)

通過引入合適的觀測誤差反饋系數(shù)，可以保證觀測器的穩(wěn)定性和時(shí)效性，從而實(shí)現(xiàn)系統(tǒng)中內(nèi)部擾動(dòng)和外部擾動(dòng)被實(shí)時(shí)估計(jì)的目的。其中反饋向量L的取值參考文獻(xiàn)[11]中將觀測器極點(diǎn)全部配置成相同重根的方法，即

s2+l1s+l2=(s+ωo)2

(12)

則向量L可用觀測器的帶寬ωo表示如下

(13)

2.2 控制器設(shè)計(jì)

準(zhǔn)確估計(jì)出系統(tǒng)擾動(dòng)后，在控制回路中施加擾動(dòng)補(bǔ)償策略，進(jìn)而將系統(tǒng)補(bǔ)償為確定性系統(tǒng)[12-14]。

通過LESO，可估計(jì)出狀態(tài)z2≈x2，取控制量

(14)

則由式(9)可得

(15)

補(bǔ)償后的系統(tǒng)如式(15)所示，其中，δ0為虛擬控制輸入，考慮到飛機(jī)的俯仰角是最終的被控量，把δ0取為工程上最常用的形式

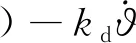
(16)

結(jié)合式(14)和式(16)，俯仰姿態(tài)控制器為

(17)

其中，?r為俯仰角的期望值；kp為比例項(xiàng)系數(shù)；kd為微分項(xiàng)系數(shù)。

由于實(shí)際被控對象的控制增益b很難獲得，控制器設(shè)計(jì)時(shí)采用與增益b相近的參數(shù)b0來代替。俯仰姿態(tài)控制器中，b0按照升降舵舵效系數(shù)取值，b0與b的差作為擾動(dòng)f中的一項(xiàng)，可被LESO估計(jì)并補(bǔ)償。最終的俯仰姿態(tài)控制器用可調(diào)參數(shù)描述為

(18)

而對應(yīng)的擴(kuò)張狀態(tài)觀測器為

(19)

基于ADRC 的俯仰姿態(tài)控制系統(tǒng)結(jié)構(gòu)如圖1所示。

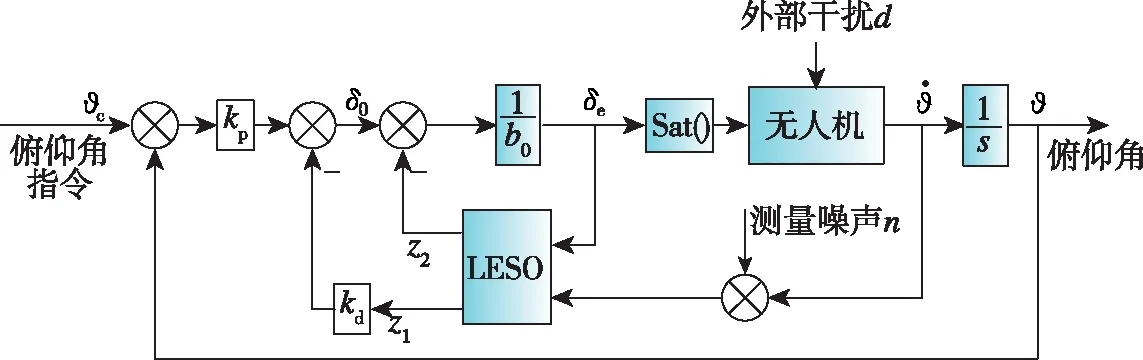
圖1 基于ADRC的俯仰姿態(tài)控制系統(tǒng)結(jié)構(gòu)圖

3 性能分析與仿真

針對某型無人機(jī)，基于ADRC設(shè)計(jì)了俯仰姿態(tài)控制器，并對其控制效果進(jìn)行仿真與分析。選取LESO觀測帶寬ωo=5，控制增益b0=-2，比例項(xiàng)系數(shù)kp=1，微分項(xiàng)系數(shù)kd=2。

選取多個(gè)狀態(tài)點(diǎn)分析LESO狀態(tài)反饋補(bǔ)償后系統(tǒng)的開環(huán)頻域特性，仿真結(jié)果如圖2所示。

由圖2可知，通過引入LESO狀態(tài)補(bǔ)償反饋，系統(tǒng)開環(huán)在低頻段具有足夠高的增益，可確保系統(tǒng)具有良好的穩(wěn)態(tài)性能。同時(shí)，在全設(shè)計(jì)剖面內(nèi)系統(tǒng)具有良好的動(dòng)態(tài)性能，相位裕度均不低于66°，幅值裕度不低于25dB。

在LESO補(bǔ)償回路的基礎(chǔ)上，加入PD控制環(huán)節(jié)，俯仰角控制閉環(huán)階躍響應(yīng)如圖3所示。

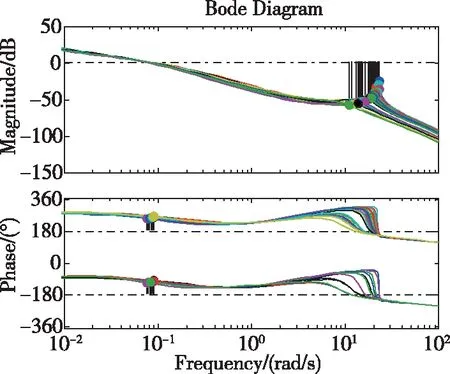
圖2 LESO反饋補(bǔ)償后俯仰角開環(huán)頻域特性

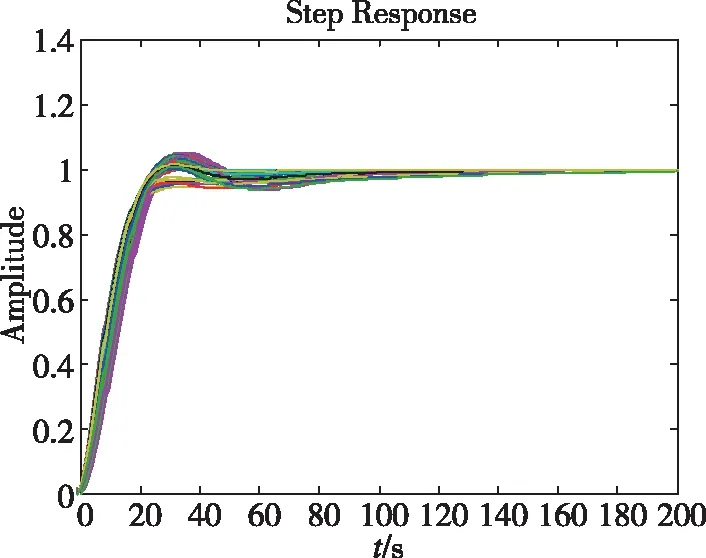
圖3 俯仰角控制閉環(huán)階躍響應(yīng)

圖3表明俯仰角閉環(huán)系統(tǒng)在各狀態(tài)點(diǎn)具有較好的指令跟蹤性能，系統(tǒng)過渡段具有良好的阻尼特性，系統(tǒng)表現(xiàn)出較強(qiáng)的魯棒性。

無人機(jī)在飛行過程中不可避免地會受到各種干擾，對于俯仰姿態(tài)控制回路，一般表現(xiàn)為紊流、突風(fēng)等不確定因素產(chǎn)生的氣動(dòng)干擾以及傳感器測量高頻脈動(dòng)量信息。分析與仿真過程中，需要評估基于ADRC的俯仰姿態(tài)控制器在這兩種典型干擾條件下的響應(yīng)特性。

經(jīng)LESO狀態(tài)反饋補(bǔ)償后，噪聲到俯仰角開環(huán)頻域特性如圖4所示。

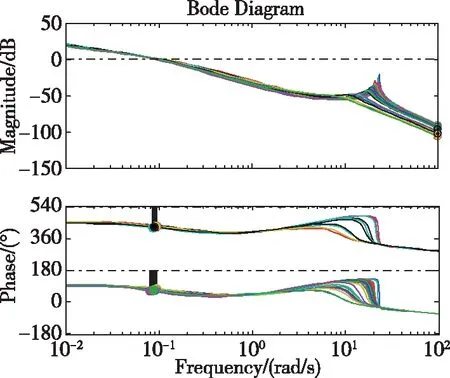
圖4 LESO反饋補(bǔ)償后噪聲到俯仰角開環(huán)頻域特性

由圖4可以看出，經(jīng)過LESO反饋補(bǔ)償環(huán)節(jié)后，高頻輸入信號產(chǎn)生的輸出量幅值得到衰減，高頻噪聲在輸出信號中產(chǎn)生的影響可被抑制，系統(tǒng)的抗干擾能力得到了增強(qiáng)。

結(jié)合非線性模型進(jìn)行六自由度仿真驗(yàn)證，無人機(jī)起飛后爬升至1000m高度，穩(wěn)定后繼續(xù)爬升至3000m高度，將俯仰力矩系數(shù)mz人為施以30%的偏差，俯仰姿態(tài)控制回路抗干擾能力及控制效果如圖5所示，其中，H-ADRC和H-ADRC-mz+分別為引入氣動(dòng)干擾前后的無人機(jī)高度指令響應(yīng)曲線。

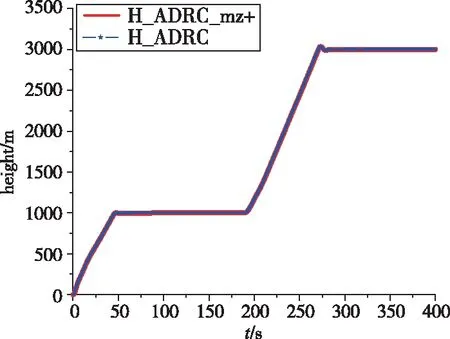
圖5 引入氣動(dòng)干擾前后控制效果對比

LESO對干擾的估計(jì)如圖6所示，其中，z2是擴(kuò)張狀態(tài)x2的估計(jì)值，即式(8)中干擾f的估計(jì)值。

圖6 LESO擴(kuò)張狀態(tài)變量

由圖5可知，對于ADRC，在加入氣動(dòng)干擾前后，其響應(yīng)曲線不變，這歸功于LESO對干擾的實(shí)時(shí)估計(jì)和補(bǔ)償。從圖6不難看出，LESO 能較好地將由風(fēng)洞實(shí)驗(yàn)偏差和高度指令改變等形成的內(nèi)、外干擾估計(jì)出來，由此說明ADRC具有良好的抗干擾特性。

4 結(jié)論

本文針對無人機(jī)俯仰姿態(tài)回路受模型參數(shù)以及外界環(huán)境變化等干擾因素影響較大的問題，基于ADRC理論設(shè)計(jì)了俯仰姿態(tài)控制器，通過LESO對系統(tǒng)各項(xiàng)不確定性干擾進(jìn)行實(shí)時(shí)估計(jì)，并以反饋量的形式引入控制輸入。性能分析與仿真結(jié)果表明：

1)LESO反饋補(bǔ)償后，系統(tǒng)的動(dòng)態(tài)和穩(wěn)態(tài)特性均得到了優(yōu)化，具有良好的跟蹤性能，可實(shí)現(xiàn)姿態(tài)穩(wěn)定控制；

2)基于ADRC方法設(shè)計(jì)的俯仰姿態(tài)控制器可快速抑制氣動(dòng)參數(shù)攝動(dòng)和傳感器噪聲等干擾因素產(chǎn)生的影響，表現(xiàn)出較強(qiáng)的魯棒性和抗干擾能力；

3)控制器設(shè)計(jì)直接針對飛機(jī)的非線性模型，在很大的包線范圍內(nèi)不需要改變控制器的結(jié)構(gòu)和參數(shù)，簡化了設(shè)計(jì)過程。