一種提高捷聯慣性/里程計組合導航系統定位精度的后處理方法

李 昂，張憶欣，季 陽，郭元江，張 澤

(北京自動化控制設備研究所，北京 100074)

0 引言

管道機器人可通過超聲波探頭等傳感器實現對海底光纜、石油天然氣等管道的無損檢測，并依靠內置的慣性測量裝置實現管道內裂紋的精準定位，在人員、衛星信號無法到達的環境中有著廣泛的應用[1-2]。現代管道鋪設時，每隔一段距離會預置一個Mark點：當管道機器人在管道內移動至Mark點時，可獲取Mark點的位置信息。考慮管道鋪設成本等因素，Mark點不會過于密集，因而Mark點間的位置需要由慣性測量裝置的導航解算獲得。

為限制慣性測量裝置在純慣性導航狀態下速度位置發散較快的問題，通常引入里程計，為系統提供相對可信的速度基準。文獻[3]利用里程計與捷聯慣導中的陀螺儀進行高精度航位推算，建立航位推算的誤差模型；文獻[4]將里程計引入管道測量裝置，初步解決了單純依靠慣導系統檢測管道精度發散的問題；文獻[5]針對復雜應用環境下由于里程計測量信息不準而導致組合導航系統精度下降的問題，利用濾波實現了故障檢測和隔離，提高了系統導航精度。此類測繪用捷聯慣性/里程計組合導航系統可實現自主連續的定位，具有較高的定位精度。

測繪用捷聯慣性/里程計組合導航系統對實時性要求較低，但對精度要求較高，可采取離線后處理方式對數據進行充分挖掘，以獲得更高的定位精度[6]。離線后處理不僅可以相應放寬對慣性器件的精度要求，節約測繪用組合導航系統的研制成本,而且可以在滿足系統精度指標的前提下，適當減少待測路徑中預置的Mark點數量[7]，縮減工程建造費用。更為重要的是，精準定位可大幅降低相關設施的維護保養難度。

本文構建了捷聯慣性/里程計組合導航系統的速度匹配Kalman濾波模型[8]和航位推算模型；基于離線后處理技術，提出了正反雙向濾波、姿態矩陣迭代和里程計刻度系數迭代相結合的后處理算法；設計了數據離線處理流程，并進行了試驗驗證。結果表明，與正向濾波方式相比，在離線處理過程中采用雙向濾波、姿態矩陣迭代和里程計刻度系數迭代算法，可將位置解算精度提高95%以上。

1 Kalman濾波模型

在傳統速度匹配濾波模型的基礎上，在狀態變量中引入里程計刻度系數誤差和安裝誤差，構建16維速度匹配Kalman濾波模型[9-10]。此模型中的里程計刻度系數誤差、航向安裝誤差角和俯仰安裝誤差角均有較高的可觀測性；在濾波過程中，此模型可消除上述誤差對系統姿態、速度和位置解算的不利影響。

系統狀態變量為

εxεyεzΘYΘZΔkΔt]T

(1)

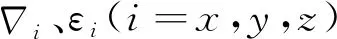
捷聯慣導系統姿態和速度誤差模型如下

(2)

(3)

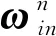
以捷聯慣導系統與里程計的北向、天向、東向速度之差作為觀測量[15]

(4)

慣導系統在地理坐標系下的速度為

(5)

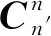
里程計的刻度系數誤差和安裝誤差已事先完成出廠標定[13]，可保證上述誤差均為小量。故里程計在地理坐標系下的速度為

(6)

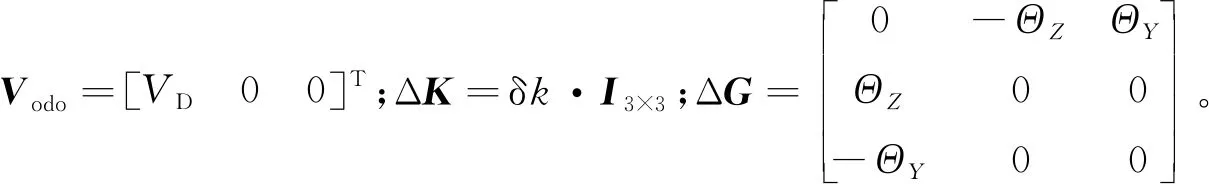
聯立式(5)和式(6)，可得

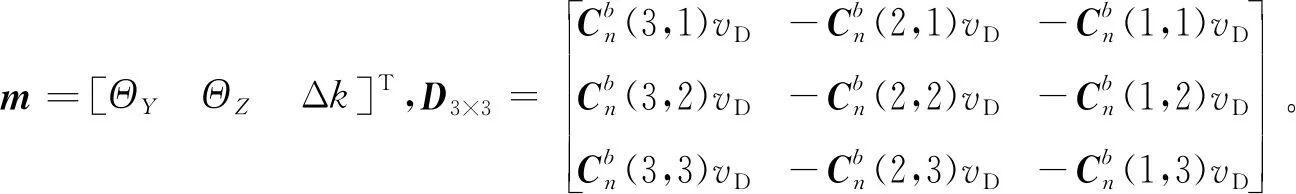
記觀測矩陣

根據狀態變量和觀測量，建立Kalman濾波微分方程

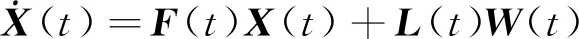
(7)

Z(t)=H(t)X(t)+V(t)

(8)

式中，F(t)為狀態微分方程系數矩陣，由式(2)和式(3)得出;L(t)為白噪聲系數矩陣;W(t)為慣性器件噪聲;H(t)為觀測矩陣;V(t)為觀測噪聲，呈高斯分布。對式(7)和式(8)進行離散化處理，可得Kalman濾波狀態方程和觀測方程，見式(9)和式(10)

xk=Φxk-1+LWk

(9)

zk=Hkxk+vk

(10)

其中，Φ為k-1時刻至k時刻的狀態轉移矩陣。

根據本節的Kalman濾波模型，在初始對準結束后，依次進行正向和反向導航及濾波解算。

2 航位推算模型

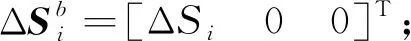
(11)

(12)

(13)

航位推算在第二次正向濾波結束后進行。從起始時刻逐段進行位置推算，并在Mark點處進行位置校正，同時對航位推算信息的誤差進行精度判斷。

3 正反雙向濾波處理

傳統的正向濾波是按時間順序，從起始點處理采樣數據直至終點。正反雙向濾波則是在正向濾波結束后，按時間倒序處理采樣數據至導航起始時刻[14-15]。如此一來，等效為采樣數據量翻倍，有利于濾波器狀態變量進一步分離，從而提高導航解算精度。

通過晃動基座粗對準，可獲取系統的初始姿態信息。隨后，構建16維速度匹配Kalman濾波模型，進行正向濾波。捷聯慣導系統正向姿態、速度和位置解算公式為

(14)

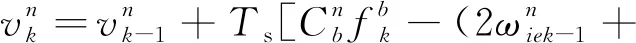
(15)

(16)

(17)

(18)

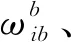
(19)

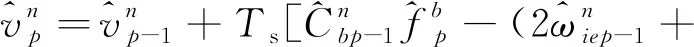
(20)

(21)

(22)

(23)

在正反雙向濾波結束后，可重置慣導速度和位置，并補償陀螺漂移、加表零偏和里程計刻度系數誤差等。通過上述處理，提高了系統再次正向濾波時的導航解算精度，從而提高了后續航位推算精度。

4 姿態矩陣迭代和里程計刻度系數迭代

從起始時刻起，依次解算相鄰兩個Mark點間的位置,進行航位推算，并觀測Mark點處的位置誤差。在每個Mark點處校正航位推算的位置，并計算里程計剩余刻度系數δk、航向剩余安裝誤差δφu和俯仰剩余安裝誤差δφx

(24)

其中，SDn、SDu、SDe、SDL分別為相鄰兩個Mark點之間里程計航位推算獲得的北向、垂向、東向以及徑向位移；dLD、dhD、dλD分別為里程計航位推算得到的緯度、高度、經度與Mark點的緯度、高度、經度的差值。

為逼近真實位置信息，在得到δk、δφu和δφx后，迭代上述系數，迭代后的系數為dk、dφu、dφx，迭代方式如下

(25)

ΔSi=(1+dk)ΔSi

(26)

(27)

因dφx和dφu均為小角度，由方向余弦矩陣，有

在上述系數完成迭代后，根據預設的位置誤差門限，判斷是否再次進行此階段的航位推算：若位置精度不滿足要求，利用迭代得到的三個參數更新姿態矩陣，重新進行此段位置計算；若位置精度滿足要求，此段離線處理工作完成，進行下一段Mark點間采樣數據的位置解算。

按此方式處理所有Mark點間的數據，直至數據結束。

5 后處理算法流程設計

本文后處理算法分為正向濾波、反向濾波、再次正向濾波、相鄰Mark點間的航位推算、姿態矩陣迭代和里程計刻度系數迭代等模塊：

首先，構建16維速度匹配Kalman濾波器，進行正向濾波，見第1節；以正向濾波結束點為起點，進行反向濾波至初始位置，見第3節；在正反雙向濾波器期間，估計慣性器件和里程計相關誤差。待反向濾波結束后，再次進行正向濾波，記錄各時刻姿態信息。最后，利用各時刻記錄的姿態信息進行航位推算，并進行姿態矩陣迭代和里程計刻度系數迭代，見第2節和第4節。依次處理所有相鄰Mark點，直至數據結束。圖1所示為后處理算法框圖。

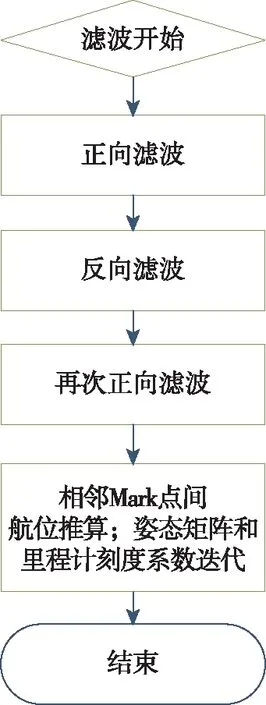
圖1 后處理算法框圖

6 試驗結果及分析

為驗證數學模型和后處理技術的正確性，進行了試驗驗證。試驗路線如下：待測路徑全程8100m，高度變化100m，每1000m設置一個Mark點。起始點經度116.1526°，緯度38.8138°；結束點經度116.2012°，緯度39.8462°。待測路徑平面圖如圖2所示。

圖2 待測路徑平面圖

設置里程計脈沖更新頻率為10Hz，慣性器件采樣頻率為200Hz。

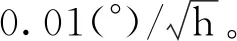
Kalman濾波周期為1s。分別采用正向濾波(forward filter)、正反雙向濾波(forward and reverse filter)、正反雙向濾波加姿態矩陣和里程計刻度系數迭代(forward and reverse filter+itera-tion)三種算法，分離器件誤差并補償。隨后，均按時間順序進行導航解算，并存儲姿態信息。最后，進行航位推算，以獲取定位結果。根據本系統慣性器件精度，預設Mark點位置誤差門限為0.1m。比較正向濾波、正反雙向濾波和本文方法三種算法的定位精度，如圖3所示。

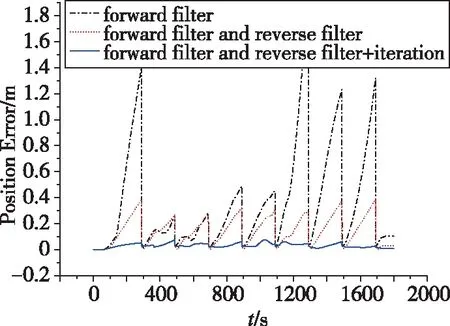
圖3 不同離線處理方法的位置精度對比

由圖3可知：

1)正向濾波和正反雙向濾波兩種方案在Mark點處對系統進行位置校正，一定程度上控制了系統的位置誤差，但隨時間累積，位置誤差增長明顯。

2)只進行慣性/里程計組合導航算法的正向濾波處理時，最大位置誤差為1.72m。

3)引入反向濾波后，最大位置誤差減小至0.39m。

4)在正反雙向濾波的基礎上，引入姿態矩陣迭代和里程計刻度系數迭代技術，使全程的定位誤差控制在0.1m以內，從而實現厘米級的定位精度。

與正向濾波方式相比，正反雙向濾波方式對陀螺和加速度計的采樣數據進行了更充分的挖掘，使狀態變量估計更精確；迭代姿態誤差矩陣和里程計刻度系數進一步提高了航位推算精度。

7 結論

本文針對測繪用捷聯慣性/里程計組合導航系統，在傳統速度匹配Kalman濾波器的基礎上，引入里程計相關誤差項，構建了16維濾波模型。提出了正反雙向濾波算法，提高了數據利用率；提出了姿態矩陣迭代和里程計刻度系數迭代算法，優化了姿態解算精度，從而提高定位精度。試驗結果表明，與傳統正向濾波相比，正反雙向濾波融合加姿態矩陣迭代和里程計刻度系數迭代算法的定位精度更高，系統定位精度提高95%以上。