動力總成懸置系統優化設計及系統穩健性分析
李聰 張帆 楊玉玲 覃臻 覃麗霜 蔣斌文



摘要:建立動力總成6自由度模型,以能量解耦為優化目標,系統頻率分布及懸置各向剛度比值為約束,懸置各向剛度為變量,采用遺傳算法對系統進行優化設計。運用Monte Carlo方法對結果可靠性進行驗證。最后通過實車測試驗證懸置系統的隔振性能。
Abstract: A 6 DOF model for powertrain mount system is established, Taking the energe decoupling method as the objective, system frequencies and stiffness ratio of each mount as constrains, stiffness of each mount as variables, the optimization of mounting system is conducted using genetic algorithm. The result reliability is checked using Monte Carlo method. Finally the performance of mounting system is verified by vehicle testing.
關鍵詞:動力總成懸置系統;能量解耦;遺傳算法;優化設計;可靠性
Key words: powertrain mount system;energe decoupling;genetic algorithm;optimization design;reliability
中圖分類號:U464.1? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文獻標識碼:A? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文章編號:1674-957X(2021)08-0014-04
0? 引言
隨著人們生活水平的提高及汽車技術和汽車工業的不斷發展,人們對汽車的乘坐舒適性要求越來越高,對汽車的振動、噪聲越來越關注。發動機是汽車最主要的振源,其振動通過懸置系統傳遞到車身上,最終影響整車振動、噪聲水平及舒適性。動力總成懸置系統除支撐動力總成外,其主要功能為隔離發動機振動,減少振動向車身的傳遞,因此懸置系統匹配設計對整車振動、噪聲及舒適性至關重要。
懸置系統隔振性能的優劣與懸置安裝位置、懸置各向剛度因素相關[1],在追求解耦率最大的同時需滿足動力總成懸置系統各階頻率合理分布及懸置結構的可制造性。在設計變量、約束條件、優化目標都較多的情況下,要做到設計最優需要一套有效的優化方法。根據目前橡膠的生產工藝及控制水平,實測懸置剛度與設計值的誤差通常在±10%以內,較大的剛度誤差可能引起系統的不穩定,因此需對系統穩健性進行分析,以保證在制造誤差內懸置系統都有較好的表現。本文采用MATLAB及ISIGHT軟件對某車型懸置系統進行優化設計,并采用Monte Carlo方法對結果的可靠性進行驗證,最后通過實車測試驗證了懸置系統的隔振性能。
1? 動力總成懸置系統六自由度模型
動力總成通過懸置系統固定到車身上,理論上動力總成及車身均具有一定剛度,橡膠懸置在三維空間上均有平動剛度及扭轉剛度,橡膠同時具有阻尼,整個動力總成懸置系統為一個復雜的彈性阻尼系統。基于以下原因并做以下幾點簡化:
①動力總成及車身剛度遠大于懸置剛度,可將動力總成及車身視為剛體;
②把橡膠簡化為3個正交方向的彈簧;
③考慮到各懸置的相對距離較近,且平動剛度較大,可忽略橡膠扭轉剛度;
④由于橡膠阻尼較小,在小幅振動的情況下可忽略橡膠阻尼。
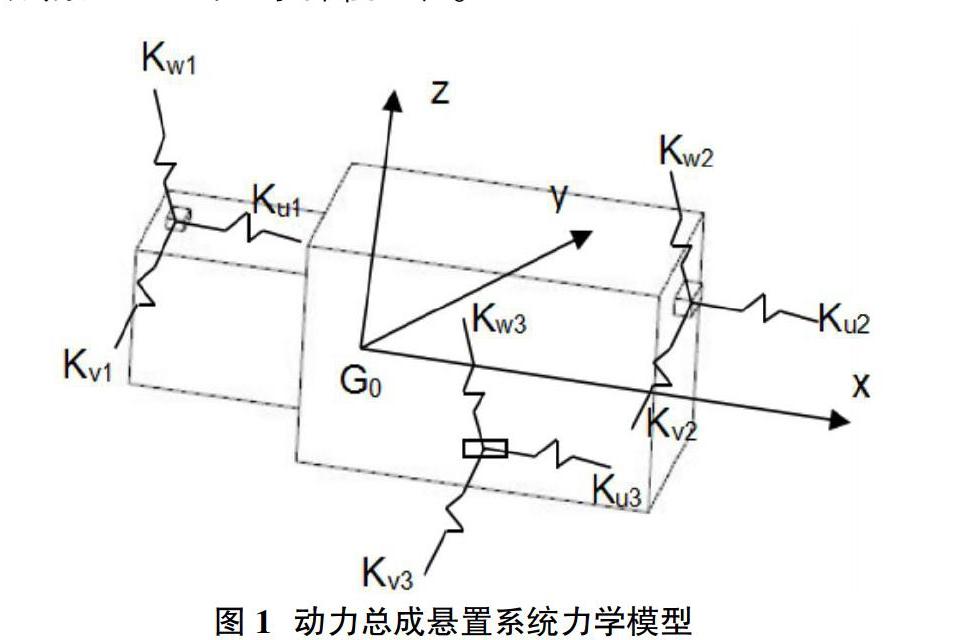
定義坐標系G0-xyz,其中G0為動力總成質心,x軸沿曲軸方向指向發動機自由端,z軸沿氣缸軸線指向缸蓋方向,y軸由右手定則確定。橡膠懸置彈性主軸坐標u、v、w分別為懸置的3條彈性主軸。
動力總成懸置系統有x、y、z3個方向的平動和繞x、y、z3個方向的轉動,多自由度振動系統的振動微分方程式為[1]:
其中:
M——系統質量矩陣;
C——系統阻尼矩陣;
K——系統剛度矩陣;
F(t)——系統所受激勵向量。
固有頻率和模態方程為[2]:
由式(2)可得系統的主振型方程:
2? 動力總成懸置系統的優化設計
動力總成6自由度運動通常相互耦合,耦合振動使得系統振動加劇,因此解耦設計成為目前動力總成設計的常用方法之一。本文以能量解耦[3]為目標對某車型懸置系統參數進行優化。
2.1 優化目標函數及目標
當動力總成懸置系統以第i階固有頻率和振型振動時,第k個廣義自由度上能量占總能量的百分比為:
其中:mkl——M的第k行l列元素;
i——系統的第i階主陣型。
動力總成6自由度中沿z軸的平動(Bounce)及繞x軸的轉動(動力總成橫置為Pitch,動力總成縱置為Roll)為最主要的2個自由度,通常要求解耦率大于90%。其余方向通常要求大于80%。
2.2 設計變量
2.2.1 懸置安裝位置{x1,y1,z1,x2,y2,z2,x3,y3,z3}
安裝位置包括各懸置的x、y、z坐標,本文實例為三點懸置,即包含左、右、后三個懸置的x、y、z坐標,共9個變量。
2.2.2 懸置安裝傾角{?茲x1,?茲y1,?茲z1,?茲x2,?茲y2,?茲z2,?茲x3,?茲y3,?茲z3}
各懸置彈性主軸與整車坐標系的夾角,本文實例為三個懸置彈性主軸與整車坐標系x、y、z坐標的夾角,共9個變量。
2.2.3 懸置剛度{Kx1,Ky1,Kz1,Kx2,Ky2,Kz2,Kx3,Ky3,Kz3}
各懸置三個彈性主軸的剛度值,本文實例為左右后三個懸置u、v、w三個彈性主軸的剛度值,共9個設計變量。
2.3 約束條件
在懸置設計時懸置的布置位置和傾角往往受到諸多限制,如三點帶防扭拉桿懸置往往要求左右懸置布置在扭矩軸附近,另外車身及動力總成安裝點以及周圍其他零件布置的需要都將懸置的安裝位置及傾角限制在一定的范圍內。
6階固有頻率首先應小于激勵力頻率的1/,只有小于激勵力頻率的1/才能起到隔振效果[4],同時各階頻率應與整車其他相關系統可能造成共振的頻率分隔開來,如6階固有頻率應避免與前懸跳動頻率的耦合,應避免人體敏感頻率5~7Hz的耦合等。
橡膠懸置受橡膠材料性能及結構限制,每種結構懸置的各向剛度比值必須限制在一定范圍內才能制造出來,否則會造成優化結果很好而實際無法制造出滿足各向剛度要求的懸置。
橡膠懸置應具備足夠的靜剛度,避免因懸置過軟造成橡膠的剪切破壞,降低懸置的使用壽命,如通常懸置的靜載位移控制在6mm以內。
2.4 優化設計
動力總成懸置系統優化涉及優化變量多、約束條件多,且同時有多個優化目標,該優化問題較為復雜,存在較多的局部最優解。采用傳統優化方法很難得出結果,或者難以得到較優的解。遺傳算法能夠有效防止優化結果限于局部最優解,得到全局最優解的概率大大增強。
遺傳算法是一種類似于生物進化的優化方法。它通過選擇、交叉、變異的循環尋求最優值。遺傳算法中采用適應度來衡量群體中各個個體在優化計算中有可能達到或接近于找到最優解的優良程度[5]。
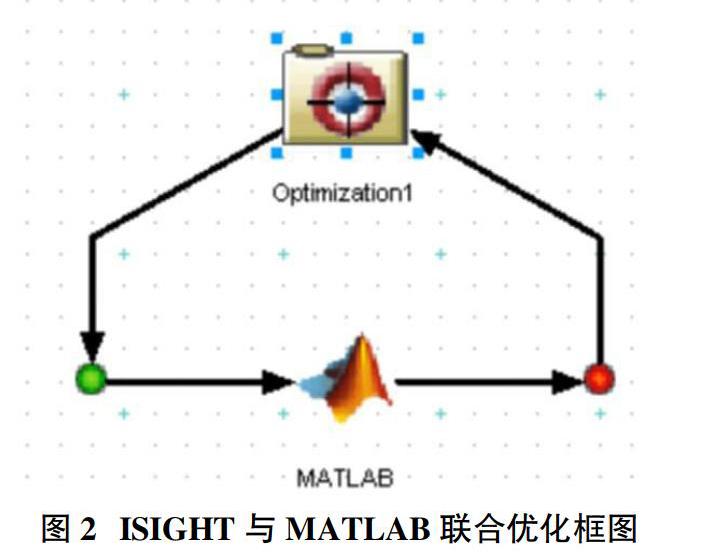
本文采用MATLAB編程對懸置系統固有頻率、解耦率進行計算,然后應用ISIGHT平臺調用MATLAB所編寫的程序進行優化設計。MATLAB編程語言便于對質量矩陣和剛度矩陣的操作,特別是對于矩陣特征值和特征向量的計算尤其方便。ISIGH是EngineousSoftware公司開發的基于WindowsNT和Unix平臺的過程集成、優化設計和穩健性設計的軟件,它可以將數字技術、推理技術和設計探索技術有效融合,并把大量的需要人工完成的工作由軟件實現自動化處理,好似一個軟件機器人在代替工程設計人員進行重復性的、易出錯的數字處理和設計處理工作。iSIGHT軟件可以集成仿真代碼并提供設計智能支持,從而對多個設計可選方案進行評估、研究,大大縮短了產品的設計周期。采用ISIGHT與MATLAB聯合優化充分結合了兩個軟件的優勢使得優化設計計算程序更加便利、高效,程序框圖如圖2所示。
本文以某車型為例,其輸入質量參數如表1所示,其中質量單位為kg,慣量參數單位為kg.m2。
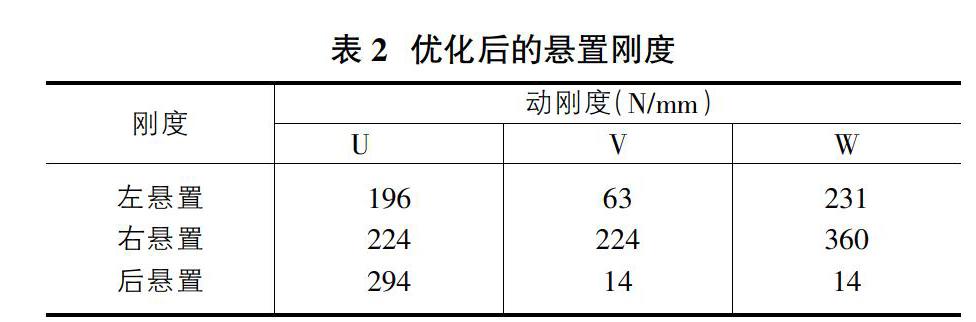
由表1參數,采用MATLAB及ISIGHT對懸置系統進行優化,由于懸置類型及受整車布置的限制,本實例僅優化懸置剛度,懸置安裝位置及安裝角度不做優化。聯合優化后的懸置剛度如表2所示,系統各階頻率及解耦率如表3所示。
該車型為三點懸置,其中左懸置為變速器側懸置,該懸置為襯套式懸置,其壓剪比為3.7滿足壓剪比3~8的范圍;右懸置為發動機側懸置,其結構為圓筒形,U、V方向剛度相同,便于制造;后懸置為防扭拉桿,V、W方向剛度為等效剛度[6]。因此左、右、后三個懸置剛度均滿足制造要求。
在表1剛度的基礎上計算左、右懸置的靜載位移分別為5.4mm和5.2mm。懸置靜載位移小于6mm,懸置耐久性可滿足要求。
由表3可知2個主要方向Bounce(上下平動)及Pitch(繞曲軸轉動)的解耦率分別達到了98.73%和96.04%,解耦效果較好。同時其他非主要方向的解耦率也都超過了95%,總體解耦效果較好。
發動機怠速轉速為750R/min,其對應二階頻率為25Hz,由表2可知除Roll方向頻率外其余頻率均小于激勵力頻率的1/(17.7Hz),考慮到Roll方向為非主要方向,結合整車振動實測沒有出現共振的情況下,頻率略高可以接受,Bounce方向的固有頻率避開了人體敏感頻率5~7Hz和前懸跳動頻率12~14Hz。
3? 動力總成懸置系統的可靠性驗證
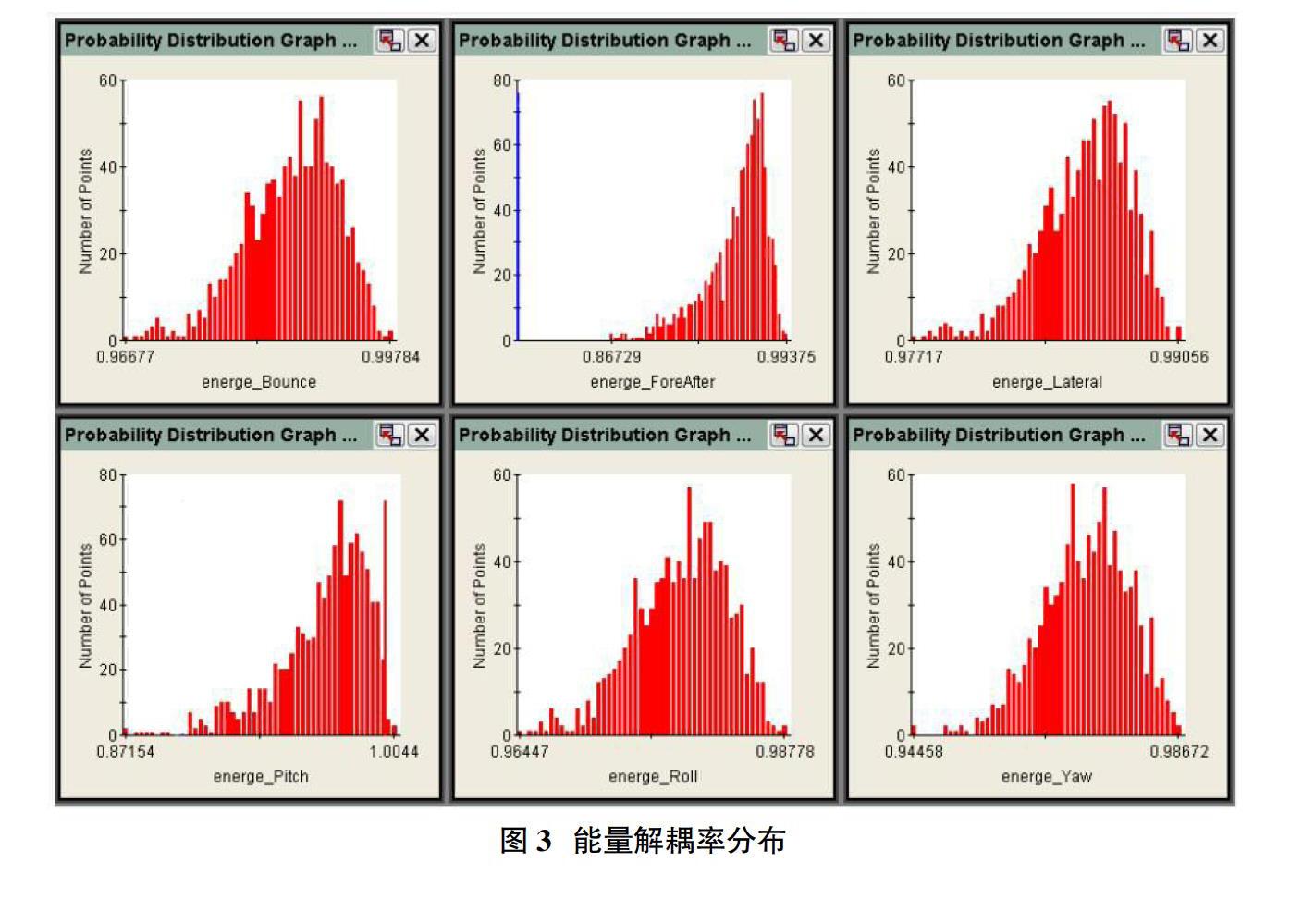
動力總成懸置系統剛度經優化后,系統解耦效果較好,但該解耦結果均是在理想剛度值的前提下得到,而實際懸置生產過程中由于制造誤差及橡膠工藝的特殊性,實測懸置剛度與設計值的誤差通常在±10%以內,在這較大的誤差范圍內,系統解耦率是否能達到要求,系統可靠性能否得到保證都需要進一步驗證。本文采用Monte Carlo法對動力總成懸置系統的可靠性進行驗證。Monte Carlo法又稱為統計試驗法,通過產生服從一定分布的隨機變量,計算響應值的分布情況,以確定變量對響應值的影響。設置各個剛度變量的數目為1000,各懸置的剛度值在±10%的范圍內變化,且滿足正態分布。經計算得到6個方向的能量解耦率如圖3所示。
由圖3可知Bounce(上下平動)方向解耦率均大于96.7%,Pitch(繞曲軸轉動)方向的解耦率主要分布在90%以上,其余各方向解耦率也都大于85%,由此可知系統穩定性較好。
4? 測試驗證
以解耦率為優化目標設計懸置系統從理論上保證了懸置系統的隔振性能,本文采用實車測試進一步證明懸置系統的隔振性能。隔振率為評價懸置系統隔振性能的重要指標,本文測試了某車型在怠速及三檔全油門工況下各懸置的隔振率如圖4和圖5所示。由圖4可知怠速工況下,左、右、后三個懸置的隔振率均達到20dB以上,即動力總成振動通過懸置后振動量衰減90%以上,懸置系統怠速隔振性能良好。由圖5可知三檔全油門工況下左懸置隔振率接近20dB,右懸置及后懸置隔振率大于20dB,因此在三檔全油門工況下懸置隔振性能較好。
5? 結論
本文采用ISIGHT及MATLAB,基于遺傳算法,以解耦率為目標對動力總成懸置系統進行設計,并采用Monte Carlo法驗證了懸置系統在考慮制造誤差情況下的可靠性,最后對設計生產出的懸置系統進行實車測試,測試結果表明懸置系統隔振性能良好,優化設計及驗證方法可靠。
參考文獻:
[1]徐石安.汽車發動機彈性支承隔振的解耦方法[J].汽車工程,1955,17(4):198-204.
[2]閻紅玉,徐石安.發動機—懸置系統的能量法解耦及優化設計[J].汽車工程,1993,15(6):321-328.
[3]趙彤航.CA1261汽車發動機懸置系統隔振的研究[D].吉林大學碩士學位論文,2002.
[4]龐劍,諶剛,何華.汽車噪聲與振動—理論與應用[M].北京:北京理工大學出版社,2006.
[5]周明,等.遺傳算法原理及應用[M].北京:國防工業出版社, 1999.
[6]上官文斌,徐馳,黃振磊,李岐,李濤.汽車動力總成懸置系統位移控制設計計算方法[J].汽車工程,2006,28(8):738-742.

