內壓圓筒斜接管的強度研究與應力評定*

劉 歡，吳喜軍，張亞寧

(榆林學院 建筑工程學院，陜西 榆林 719000)

隨著人們生活水平的提高和現代工業的迅猛發展，對壓力容器性能要求也變得越來越高。壓力容器，顧名思義，是含有壓力的容器，根據內部壓力和外部壓力的大小可以分為內壓容器和外壓容器[1]。內壓容器根據設計壓力的大小可以分為低壓容器、中壓容器、高壓容器和超高壓容器等。壓力容器主要組成部分為筒體和封頭，由于工藝過程或者檢修需要在筒體或者封頭上開孔，開孔可以分為單一開孔和開孔并帶有接管2種形式，而開孔并帶有接管應用最為廣泛[2-3]。

在壓力容器上開孔破壞了結構的連續性，在內壓作用下，開孔部位除了承受薄膜應力外，還承受不連續應力，因此，總體應力增大，容易發生強度失效，屬于危險區域。開孔接管作為壓力容器的一個重要組成部分，其性能的優劣直接影響著整臺壓力容器的綜合性能。有關壓力容器開孔接管的應力分析一直都是各個領域尤其是能源化工行業的一項最基本也是最重要的探索和任務，在保證安全的前提條件下，盡可能做到經濟，減少成本消耗，因此對壓力容器開孔接管區域應力強度分析與設計越來越受到國內外學者的關注[4-7]。在壓力容器的應力分析研究中，需要進行比較全面的應力分析和強度校核，常規的應力解析不能滿足要求，ANSYS有限元方法不需要進行大量的理論數據計算實驗，既提高了效率，又節省了成本，成為壓力容器應力分析及安全評定的重要方法之一[8-10]。因此，利用ANSYS有限元方法對壓力容器開孔接管區域進行應力分析具有很高的經濟效益。

國內外學者主要對正交開孔接管進行分析，考察幾何參數和載荷對其應力分布的影響，對斜接管研究較少，且其受力情況十分復雜[11-13]。因此作者以斜接管為研究對象，借助ANSYS有限元方法對不同結構參數下的軸向斜接管大開孔結構進行建模并進行數值模擬，從模擬的結果中對應力分布規律進行研究，分析改變不同結構參數對斜接管應力分布的影響，所得結論對內壓圓筒斜接管的應力分析具有一定的研究意義和參考價值。

1 有限元分析

1.1 工作條件及結構參數

筒體內徑D=400 mm，筒體厚度T=15 mm，接管內徑d=350 mm，斜接管厚度t=10 mm，斜接管長度l=850 mm，筒體軸線與接管軸線夾角θ=45°，不考慮邊緣效應的影響，取筒體長度L=1 500 mm。筒體和接管材料均為不銹鋼0Cr18Ni9，彈性模量E=2.06×105MPa，泊松比μ=0.3，屈服強度σs=205 MPa，抗拉強度σb=520 MPa，許用應力[σ]=137 MPa。由于模型幾何尺寸和載荷具有對稱性，因此有限元模型可利用結構的對稱性取開孔接管區的1/2建模，利用ANSYS交互模式直接生成實體模型，再通過網格劃分來獲得三維有限元模型。所建幾何模型見圖1。

圖1 斜接管模型

1.2 網格劃分

采用邊長為10 mm的等邊三角形網格進行劃分，并對筒體和接管連接附近區域進行網格細化。網格劃分的節點數為130 000，網格劃分的單元數為48 000。

1.3 邊界條件及載荷

在分析中借鑒設備的實際操作情況，忽略了重力、風載荷、雪載荷、物料重力、溫度載荷和地震載荷，主要考慮內壓載荷。分析過程中，基于所建模型在空間坐標系的位置添加約束條件。因為接管的長度足夠長，遠大于接管邊緣應力衰減長度，所以在x方向可以不施加約束，只需考慮y和z方向的約束即可[14-15]。

2 有限元模擬結果及其應力評定

以內壓圓筒斜接管為研究對象，借助ANSYS有限元分析軟件，通過改變筒體內徑、接管內徑、筒體厚度、接管厚度、接管與筒體夾角5個參數，考察其對圓筒軸向斜接管開孔接管區最大等效應力的影響，并對其進行應力安全評定。

2.1 接管內徑對最大等效應力的影響

保持筒體內徑D=400 mm、筒體厚度T=15 mm、接管厚度t=10 mm，筒體軸線與接管軸線夾角θ=45°，接管內徑d=150、200、250、300、350 mm，考察接管內徑對內壓圓筒斜接管最大等效應力的影響，見圖2。

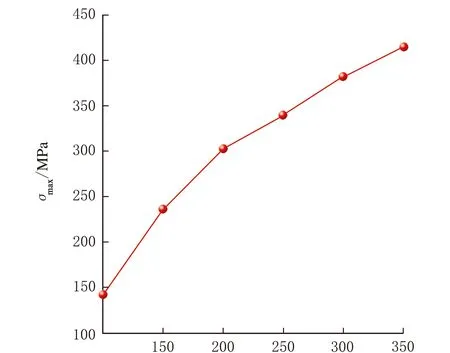
d/mm圖2 不同接管內徑下最大等效應力的變化曲線圖

由圖2可知，隨著內壓圓筒斜接管內徑d的增大，最大等效應力呈增大的趨勢。這是由于開孔系數作為影響壓力容器最大等效應力的重要因素，與接管內徑d成正比，因此，接管內徑d越大，開孔系數越大，不連續程度增加，最大等效應力越大。

2.2 接管厚度對最大等效應力的影響

保持筒體內徑D=400 mm、筒體厚度T=15 mm、接管內徑d=100 mm，筒體軸線與接管軸線夾角θ=45°，接管厚度t=6、8、10、12、14 mm，考察接管厚度對內壓圓筒斜接管最大等效應力的影響，見圖3。

t/mm圖3 不同接管厚度下最大等效應力變化曲線圖

由圖3可知，隨著內壓圓筒斜接管厚度t的增大，最大等效應力呈減小的趨勢。這是由于斜接管厚度t越大，接管強度增強，抗壓能力增強，力學性能優良，因此最大等效應力減小。

2.3 筒體軸線與斜接管軸線的夾角對最大等效應力的影響

保持筒體內徑D=400 mm、筒體厚度T=15 mm、接管內徑d=100 mm，接管厚度t=10 mm，筒體軸線與接管軸線夾角θ=30°、45°、60°、75°、90°，考察筒體軸線與接管軸線夾角θ對內壓圓筒斜接管最大等效應力的影響，見圖4。

θ/(°)圖4 不同夾角下最大等效應力變化曲線圖

由圖4可知，隨著筒體軸線與接管軸線夾角θ的增大，最大等效應力呈減小的趨勢。這是由于筒體軸線與接管軸線夾角θ越大，筒體和接管由于幾何尺寸所產生的不連續程度越小，因此最大等效應力減小。

2.4 筒體內徑對最大等效應力的影響

保持筒體厚度T=15 mm、接管內徑d=250 mm，接管厚度t=10 mm，筒體軸線與接管軸線夾角θ=45°，筒體內徑D=150、200、250、300、350、400 mm，考察筒體內徑D對內壓圓筒斜接管最大等效應力的影響，見圖5。

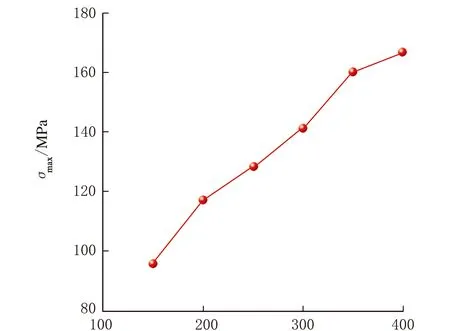
D/mm圖5 不同筒體內徑下最大等效應力變化曲線圖

由圖5可知，隨著筒體內徑D的增大，最大等效應力呈增大的趨勢。這是由于開孔系數作為影響壓力容器最大等效應力的重要因素，與筒體內徑D成正比，筒體內徑D越大，開孔系數越大，相對應的應力集中系數增大，因此最大等效應力增大。

2.5 筒體厚度對最大等效應力的影響

保持筒體內徑D=400 mm、接管內徑d=100 mm，接管厚度t=10 mm，筒體軸線與接管軸線夾角θ=45°，筒體厚度T=12、14、16、18、20 mm，考察筒體厚度對內壓圓筒斜接管最大等效應力的影響見圖6。

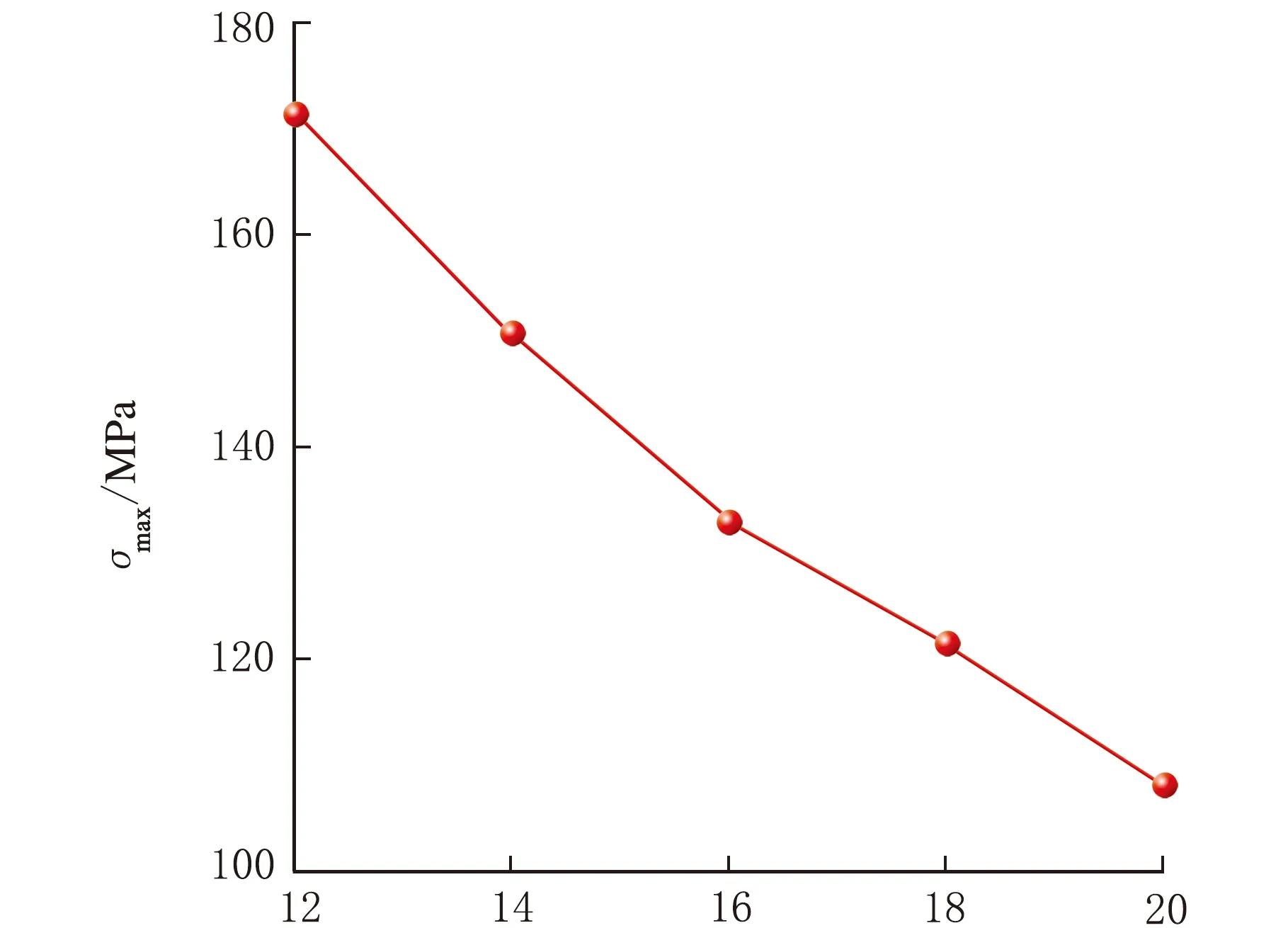
T/mm圖6 不同筒體厚度下最大等效應力的變化曲線圖

由圖6可知，隨著筒體厚度T的增大，最大等效應力呈增減小的趨勢。這是由于筒體厚度T越大，開孔系數減小，相對應的應力集中系數減小，因此最大等效應力減小。

3 應力集中系數的計算

引入應力集中系數K，計算公式見式(1)。

K=σmax/σθ

(1)

式中：σmax為最大等效應力，MPa；σθ為周向應力，MPa。

不同結構參數下模型的最大等效應力集中系數見表1和表2。

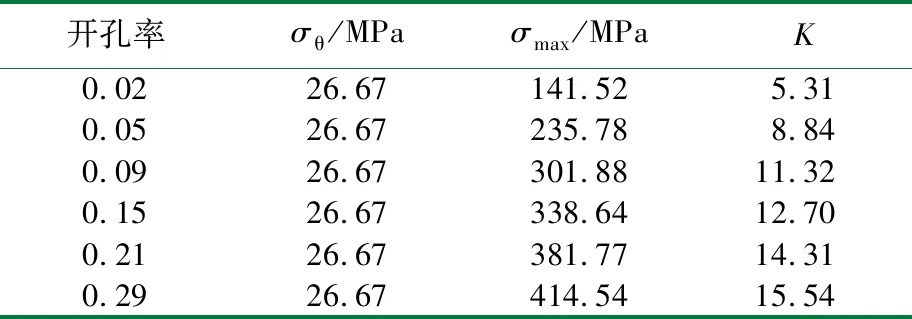
表1 改變開孔率下的應力集中系數

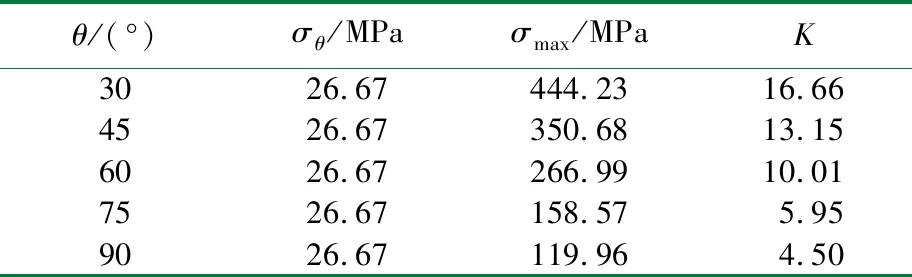
表2 改變夾角下的應力集中系數

由表1可知，開孔率越大，應力集中系數越大，說明在保持其他條件不變的情況下，開孔率越大，應力集中現象越明顯，而開孔率的大小與接管內徑成正比，因此控制開孔率可以簡化為控制接管內徑。

由表2可知，應力集中系數在θ=30°～75°下降的速度十分急劇，在θ=75°～90°下降速度比較平緩，應力集中系數在θ=30°時最大，在θ=90°時降到最小，因此在設備生產制造中，可以把角度適當控制在θ=75°～90°，設計出來的設備力學性能好。

4 結 論

(1)隨著接管內徑d、筒體內徑D的增大，最大等效應力呈增大的趨勢；隨著接管厚度t、筒體軸線與斜接管軸線的夾角θ、筒體厚度T的增大，最大等效應力呈減小的趨勢；

(2)通過應力集中系數的計算，可以控制接管內徑和夾角θ=75°～90°減小應力集中系數。