發揮“圖形語言”功能提升數學建模能力
張姝晗 黃蓮花


小學數學教學要引導學生從千頭萬緒的事物中發現規律,提升建模能力。這個過程,“圖形語言”發揮著重要的功能作用,它可以為正確思維與客觀現實搭起一座橋梁。
一、從復雜到簡潔:發揮“圖形語言”的簡化功能
小學生數學學習以具體形象思維為主,但往往因文字語言的抽象性或情境本身的復雜性給學生體驗數學模型帶來不小的挑戰。而“圖形語言”在將“復雜問題簡單化”的過程中發揮了一定的作用。因此,教師要遵循學生的認知特點和思維方式,重視引導學生將復雜問題或繁雜情境借用圖形進行思考,以降低難度,幫助學生順利把握概念本質,并予以清晰表達。
如在“長方形面積計算”的拓展運用環節,筆者創設了問題情境:“希望小學的操場是一個長方形,原來長60米,寬30米,擴建后,寬將增加10米。擴建后的操場面積有多大?”僅從文字語言的描述,要清晰地理解擴建后的操場面積如何計算,對于大部分學生而言還是有一定難度的。筆者啟發思考:“擴建后的操場是什么形狀?你能不能畫圖清晰地呈現出來?”然后指導學生按如下步驟畫出圖形,重點指導“寬將增加10米”如何在圖上畫出。
動態呈現出直觀圖后,學生的思路一下子清晰起來了,不僅理解了擴建后的操場是一個長不變、寬為“30+10”米的長方形,而且發現了一種新的思路,那就是擴建后的操場面積還可以看成是由“原來的長方形與增加后的長方形的面積之和”。打開了思路,問題的解決就變得簡單容易了。可見,圖形語言在這里起到了簡化的功能。
教師在引導學生經歷體驗感悟“圖形語言”的簡化功能后,要及時幫助學生進行梳理,以獲得一定的成就感,使之成為學生后續解決復雜問題的有效策略。這個過程能促進學生建模能力的提升。
二、從現實到數學:發揮“圖形語言”的媒介功能
模型思想的核心在于建模,而建立模型思想的關鍵在于學生具有將現實問題與數學內容進行構建關聯的主動意識和操作能力。這個關聯的過程,對小學生已有經驗和綜合運用知識能力是一個極大的考驗。發揮“圖形語言”作為媒介功能,能夠幫助學生順利完成從現實到數學知識的躍進,進而不斷提升學生問題解決的能力。
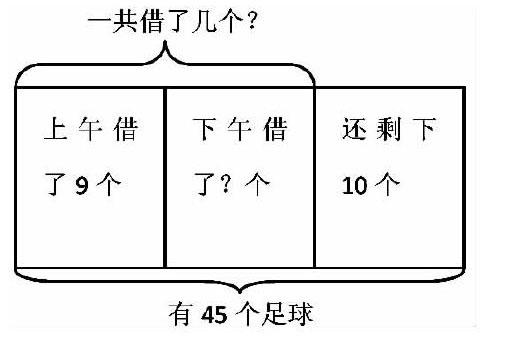
如在一年級學生學習了總數與部分數之間的數量關系后,筆者設置了一道練習:體育室里有45個足球,上午借走了9個,下午借了一些后,總共還剩10個,一共借走了幾個足球?筆者讓學生先嘗試自己解決,發現大部分學生無從下手。于是,筆者引導學生借助畫圖幫助解決后,出現了如下幾種答案:(1)45-9-10=26(個);(2)45-9-10=26(個),26+9=35(個);(3)45-10=35(個)。
然后,筆者組織學生結合圖示對各自算法進行說理后,提問:“第二種和第三種兩種方法,你喜歡哪種?為什么?”生:“我喜歡第三種,一步就能解決問題,太簡單了。”生:“我也喜歡第三種,不過這個算式,要畫圖后我才明白呢。”筆者:“為什么畫圖后你才明白呢?”生:“畫圖后,我發現原來的45個足球可以分成兩部分,一部分是‘剩下的10個,另一部分就是‘一共借了幾個。要求一共借了幾個,只要用總數45個減去剩下的10個就行了。”生:“我用45-9-10=26,只是求出了下午借了幾個。還得跟上午借出的9個合并,才能求出一共借出的足球個數。”生:“我發現了一個秘密,原來我們都是根據信息一步一步列出算式解決問題的,畫圖后,我發現了從要解決的問題去想,需要的信息就比較簡單了。”筆者:“是啊,解決問題有兩種思路,可以從已知信息中一步一步解決問題,也可以從問題入手,找需要的信息。看來圖形很有用處,不僅能幫助理解題意、講清道理,還讓我們發現了更簡單快捷的算法。”
面對抽象的數量關系,借助圖形表征能降低理解的難度。這個過程,學生既實現了思維從具象到抽象的轉化,也進行了數學發散思維與建模的實踐。
三、從數量到關系:發揮“圖形語言”的遷移功能
數學基本概念包括數學研究對象的定義、刻畫研究對象關系的術語和計算方法等,是基于現實抽象的基礎上形成的。那么,在教學這些基本概念的過程中,不僅要重視引導學生關注研究對象本身,還要關注研究對象之間的關系。這個過程,可以充分發揮“圖形語言”的助推遷移功能。
如教學人教版二下“除法的初步認識”時,筆者通過圖片(圖略)設置問題情境:20個竹筍每4個放一盤,能放幾盤。引導學生通過動手操作,呈現出能放5盤這一結果后,引出除法算式20÷4=5,然后結合圖示引導學生理解算理,知道算式中每個數所表示的含義。隨后,筆者變換不同情境圖讓學生分一分、填一填,并列式15÷3=5、15÷5=3。到此,引導學生觀察比較三個算式,及時抽象出“包含”除法的含義,即“求一個數里面包含著幾個另一個數”可以用除法計算,讓學生對“包含除”這一概念有較為深刻的認識。
教學到此,看似完成任務了。其實,不妨繼續往下思考:“包含除”與“平均除”有著怎樣的聯系?除法又與乘法有著怎樣的關系?作為教師,如何引發學生進一步思考,從中獲得感悟?筆者是這樣進行的,先出示如下(1)(2)兩個圖式,要求先分一分,然后寫出除法算式。反饋交流后,筆者提問:“兩個圖的解答都用除法計算,有什么不同?”接著,出示如下第(3)圖,提問:“你能看圖列出幾個算式?”學生列出12÷4=3、12÷3=4、3×4=12后,筆者提問為什么可以這樣列式。
通過互動,學生初步理解這三個算式中的三個數分別表示圓圈的總個數、每份的圓圈個數和分成的份數。如果知道了總個數和每份的個數或者分成的份數,求分成的份數或者每份的個數,都可以用除法算式表示;反過來,如果知道了每份的個數和分成的份數,求總個數就可以用乘法計算。緊接著,引導學生觀察三個算式,依據各部分名稱,學生感受到“除數4和商3相乘正好得到被除數12”“除法算式中的除數和商相當于乘法算式中的兩個因數,被除數相當于積”。在后面的學習中,學生自然地從除法算式聯想到乘法算式,在解釋運用中理解了乘除法之間的關系,建構了認知的經驗,提升了建模的意識和能力。
(作者單位:福建省廈門第二實驗小學 福建省廈門市文安小學 本專輯責任編輯:王振輝)

