正確認識動生電磁感應現(xiàn)象中的功能關(guān)系成立的參考系

閆來貴

（江蘇省海安市曲塘中學，江蘇 海安 226600）

1 問題的提出

功能關(guān)系是一條很重要的物理規(guī)律，即功是能量轉(zhuǎn)化的量度.不同的功對應著不同形式的能量轉(zhuǎn)化，如物體所受外力的總功是物體動能變化的量度，重力的功是物體重力勢能變化的量度.

在物理教學和教輔資料中，關(guān)于動生電磁感應現(xiàn)象中的功能關(guān)系，一般總結(jié)為：導體棒做切割磁感線運動時，克服安培力做的功是其它形式的能轉(zhuǎn)化為電能的量度，即電路獲得的電功率等于導體棒克服安培力做功的功率.

對上述動生電磁感應現(xiàn)象中的功能關(guān)系，資料和文獻一般在磁場不動、導體棒（單棒）運動的特殊情境下，給出了嚴格的證明.［1］所以，對于磁場不動、導體棒運動的情境下，此功能關(guān)系的正確性毋庸置疑，我們在分析相應的問題（磁場不動）時屢試不爽.

但文獻［1-2］對2007年上海卷一道高考題的研究中指出：當磁場運動、導體棒也運動并做切割磁感線的情形下，此功能關(guān)系不再成立.筆者對文獻［1-2］的這種觀點持懷疑態(tài)度，即上述動生電磁感應現(xiàn)象中的功能關(guān)系，只在靜止的穩(wěn)恒磁場中做切割磁感線的導體棒成立，對運動磁場中做切割磁感線的導體真的不成立嗎？

如何正確認識動生電磁感應現(xiàn)象中的功能關(guān)系及其成立的條件呢？

2 相關(guān)文獻對動生電磁感應現(xiàn)象中的功能關(guān)系貌似不成立的高考真題研究回顧

例1.（2007年上海卷）如圖1所示，光滑的平行長直金屬導軌置于水平面內(nèi)，間距為L、導軌左端接有阻值為R的電阻，質(zhì)量為m的導體棒垂直跨接在導軌上.導軌和導體棒的電阻均不計，且接觸良好.在導軌平面上有一矩形區(qū)域內(nèi)存在著豎直向下的勻強磁場，磁感應強度大小為B.開始時，導體棒靜止于磁場區(qū)域的右端，當磁場以速度v1勻速向右移動時，導體棒隨之開始運動，同時受到水平向左、大小為f的恒定阻力，并很快達到穩(wěn)定速度，此時導體棒仍處于磁場區(qū)域內(nèi).

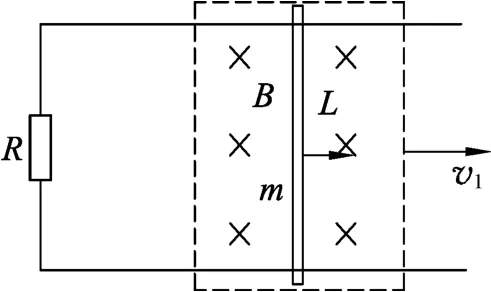
圖1

（1）求導體棒所達到的恒定速度v2；

（2）為使導體棒能隨磁場運動，阻力最大不能超過多少？

（3）導體棒以恒定速度運動時，單位時間內(nèi)克服阻力所做的功和電路消耗的電功率各為多大？

2.1 關(guān)于第（3）問的解析

導體棒所達到的恒定速度大小和導體棒達到恒定速度v2后所受到的安培力大小分別為

關(guān)于第（3）問，導體棒達到恒定速度v2后安培力做功功率、單位時間內(nèi)克服阻力所做的功和電路消耗的電功率分別為［1-2］

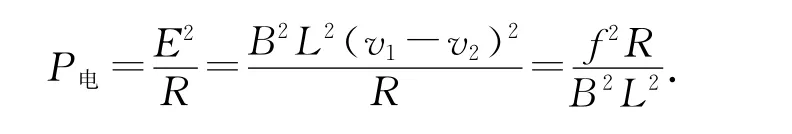
關(guān)于第（3）問，題目中沒有特別指明參考系，一般默認是以地面為參考系的.因此，上述解析結(jié)果正確無誤.

2.2 相關(guān)文獻進一步分析時出現(xiàn)的困惑

文獻［1-2］指出：在解這道題時，學生如果從功能關(guān)系出發(fā)，就會發(fā)現(xiàn)導體棒做勻速運動時，由于P安=P克阻，即安培力做的功等于克服阻力做的功，安培力做功消耗的能量轉(zhuǎn)化為摩擦生熱，根據(jù)功能關(guān)系電路中獲得的電能從何而來呢？另外，在這道題中，由于P電≠P安，因此動生電磁感應現(xiàn)象中的功能關(guān)系“導體棒做切割磁感線運動以穩(wěn)定速度運動時，電路獲得的電功率等于導體棒克服安培力做功的功率”，在本題磁場運動的情境下不適合了.

2.3 相關(guān)文獻對上述困惑的解釋

文獻［1-2］對上述困惑的解釋：由牛頓第三定律，磁場受到等大的安培力（準確的說，應該是：與安培力等大的反作用力.筆者注），方向與磁場的運動方向相反，所以磁場克服安培力做功的功率為P克安=F安v1=fv1.從第（3）問解析中的幾個表達式可以得出.即電路中所獲得的電功率在數(shù)值上等于磁場克服安培力做功功率與安培力對棒做功功率之差.

可見，本題中動生電磁感應現(xiàn)象中的功能關(guān)系“導體棒做切割磁感線運動時，克服安培力做的功是其它形式的能轉(zhuǎn)化為電能的量度，即電路獲得的電功率等于導體棒克服安培力做功的功率”是不可靠的，它不具有普遍性.

3 如何正確認識動生電磁感應現(xiàn)象中的功能關(guān)系及其成立的條件呢

要正確認識動生電磁感應現(xiàn)象中的功能關(guān)系及其成立的條件，需要從產(chǎn)生動生電磁感應現(xiàn)象的微觀本質(zhì)（非靜電力做功）中去理解，唯有如此才能真正看清此功能關(guān)系成立的條件是什么.

3.1 洛倫茲力的一個分力f 1對導體棒中所有電子做功的功率與電路消耗的電功率的關(guān)系

2007年上海高考題中，當導體棒達到恒定速度（是以地面為參考系的速度）v2時，導體棒相對于磁場靜止的觀察者為參考系，其速度大小為v相對=（v1-v2），方向向左，如圖2所示.設導體棒中單位體積內(nèi)的自由電子數(shù)為n，導體棒的長度和橫截面積分別為L、S.

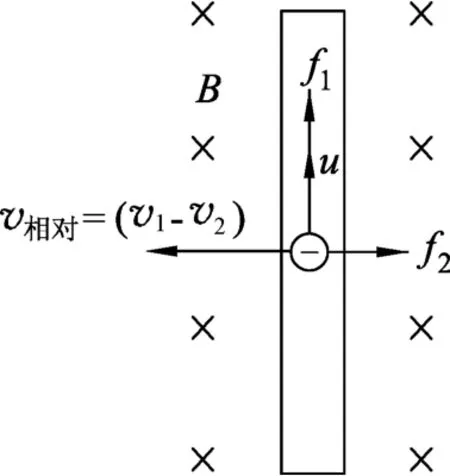
圖2 微觀分析

微觀上，導體棒中的電子受到的洛倫茲力的一個分力沿棒向上，其大小為f1=e（v1-v2）B，［3］它是棒中產(chǎn)生動生電動勢的非靜電力，根據(jù)電動勢定義，動生電動勢為［4］

（4）式說明：微觀上洛倫茲力的一個分力f1（非靜電力）對導體棒中所有電子做功的功率P1，等于宏觀上電路消耗的電功率P電=EI，也等于宏觀上導體棒克服安培力做功的功率P克安=BILv相對=BIL（v1-v2）.需要注意的是：這里克服安培力做功的功率，是以相對于磁場靜止的觀察者為參考系的.

3.2 洛倫茲力的另一個分力f 2對導體棒中所有功電子做功的功率與安培力對導體棒做功的功率的關(guān)系

微觀上，由于導體棒中電子的定向移動，電子受到向右的洛倫茲力f2=eu B，其對導體棒中所有電子做負功的功率為

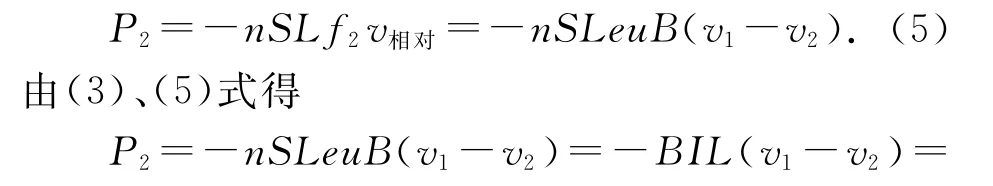
（6）式說明：微觀上洛倫茲力的另一個分力f2對導體棒中所有電子做功的功率P2的絕對值，等于宏觀上電路消耗的電功率P電=EI，也等于宏觀上導體棒克服安培力做功的功率P克安=BILv相對=BIL（v1-v2）.仍需要注意的是：這里克服安培力做功的功率，是以相對于磁場靜止的觀察者為參考系的.

由（2）、（5）式可知：P1+P2=0，這表明：洛倫茲力的兩個分力的總功率為0，即洛倫茲力永不做功，即電路中獲得的電能并不是磁場本身提供的，而是磁場運動中克服安培力的反作用力需要其它外力對磁場做功，消耗其它形式的能量轉(zhuǎn)化而來的，這與前面所述的文獻［1-2］對困惑的解釋一致.

綜上所述，當磁場運動時，動生電磁感應現(xiàn)象中的功能關(guān)系“導體棒做切割磁感線運動時，克服安培力做的功是其它形式的能轉(zhuǎn)化為電能的量度，即電路獲得的電功率等于導體棒克服安培力做功的功率”也是成立的.

但需要特別注意的是：由于功具有相對性，功的計算與參考系有關(guān).動生電磁感應現(xiàn)象中的功能關(guān)系中，克服安培力做的功（或功率）是以相對于磁場靜止的觀察者為參考系的.

即動生電磁感應現(xiàn)象中的功能關(guān)系成立的條件是：以相對于磁場靜止的觀察者為參考系的.

顯然，文獻［1-2］和部分師生產(chǎn)生困惑和錯誤認識的根源在于，對動生電磁感應現(xiàn)象中的功能關(guān)系成立的參考系是不清楚的，誤認為是地面參考系了.